说明
工作之后重新刷算法,主要是用java刷算法,读书期间用python/c++刷算法偏多,一来python写起来快很多,而来c++的性能有笔java高很多,所以当时java显得不伦不类。但因为现在的工作语言是java,所以开始用java进行刷算法。同时可以试试go吧,因为刷算法是快速熟悉一门语言的途径,想了解下go,所以刷算法的时候可以用用go。
总结
解1
nums2拼接到nums1的尾部,直接sort
java
解2:双指针
代码详情
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = 0, p2 = 0;
int[] sorted = new int[m + n];
int cur;
while (p1 < m || p2 < n) {
if (p1 == m) {
cur = nums2[p2++];
} else if (p2 == n) {
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for (int i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
}
}
|
my solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
if (m == 0) {
System.arraycopy(nums2,0, nums1, 0, n);
}
if (n == 0) {
return;
}
int[] combined = new int[m + n];
int oneIdx = 0;
int twoIdx = 0;
for (int i = 0; i < m + n; i++) {
if (oneIdx < m && twoIdx < n) {
if (nums1[oneIdx] < nums2[twoIdx]) {
combined[i] = nums1[oneIdx];
oneIdx += 1;
} else {
combined[i] = nums2[twoIdx];
twoIdx += 1;
}
continue;
}
if (twoIdx >= n && oneIdx < m) {
combined[i] = nums1[oneIdx];
oneIdx += 1;
continue;
}
if (oneIdx >= m && twoIdx < n) {
combined[i] = nums2[twoIdx];
twoIdx += 1;
}
}
System.arraycopy(combined, 0, nums1, 0, m + n);
}
}
|
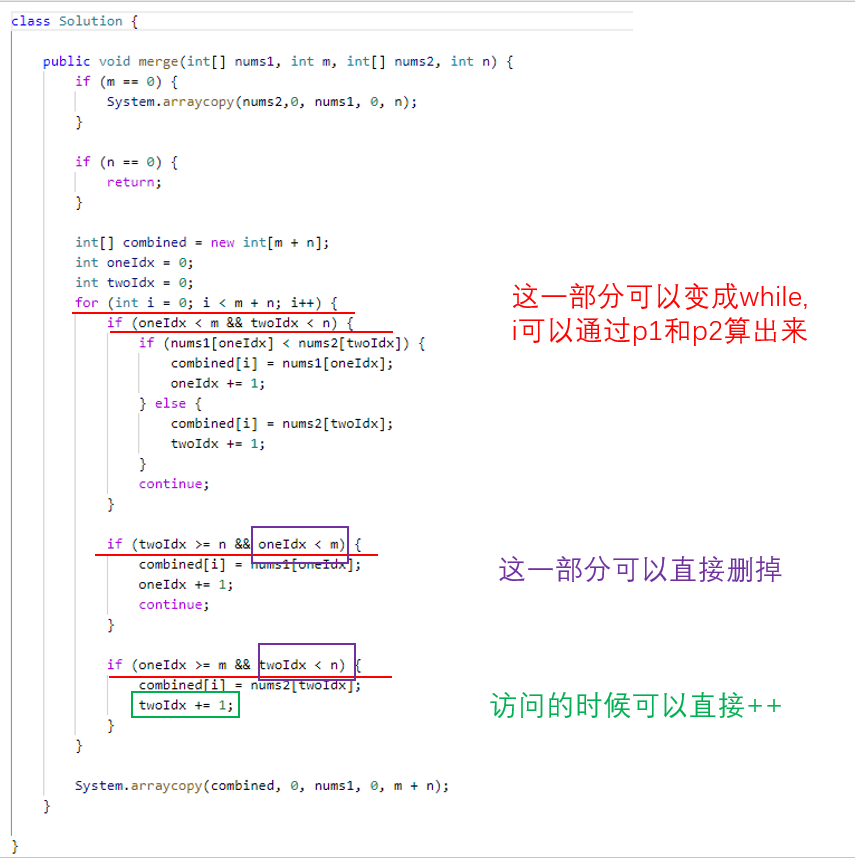
我的代码待优化的地方

解3:逆向双指针
官方题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = 0, p2 = 0;
int[] sorted = new int[m + n];
int cur;
while (p1 < m || p2 < n) {
if (p1 == m) {
cur = nums2[p2++];
} else if (p2 == n) {
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for (int i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
}
}
|
拓展阅读
- 快速排序的时间复杂度:快速排序的最坏运行情况是 O(n²),比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn),且 O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
我的方法
尾移法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public int removeElement(int[] nums, int val) {
int removeNum = 0;
if (nums.length != 0 && nums[0] == val) {
removeNum++;
}
for (int i = 1; i < nums.length; i++) {
nums[i - removeNum] = nums[i];
if (nums[i] == val) {
removeNum++;
}
}
return nums.length - removeNum;
}
}
|
我的思路可以优化的地方

1
2
3
4
5
6
7
| public int removeElement(int[] nums, int val) {
int idx = 0;
for (int x : nums) {
if (x != val) nums[idx++] = x;
}
return idx;
}
|
双指针
代码详情
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public int removeElement(int[] nums, int val) {
int left = 0;
int right = nums.length;
while (left < right) {
if (nums[left] == val) {
nums[left] = nums[right - 1];
right--;
} else {
left++;
}
}
return left;
}
}
|
一种分析
官方题解
这个数组翻转的方法事实上揭示了以下一些计算机科学和算法设计中的重要思想和技巧:
- 分治思想:
- 通过将复杂的整体问题拆解成几个部分,并分别解决这些部分,再将这些部分的解组合起来以得到整个问题的解。
在这道题中,我们通过将整体翻转再进行局部分段翻转的方法,将整个问题分解为几个更小的且相对简单的子问题。
- 空间优化:
- 在旋转数组时,最初可能会想到使用额外的空间来存储中间状态(例如临时数组)。而通过翻转的方法,不需要使用额外的空间来实现原地交换,从而节省了内存。
- 这种空间优化方法往往是高效算法的一个显著特征。
- 来源与去后的一一对应关系:
翻转方法巧妙地利用了数组元素在物理顺序上的对应关系,通过全局和局部的翻转完成了元素位置的调整。
在解决矩阵和字符串问题时,这种一一对应的调整方法也是一个强有力的工具。
数学性质与模运算:
运用了模运算来简化处理循环结构的问题。数组右移 k 次相当于右移 k mod n 次(其中 n 是数组长度),模运算有效地避免了冗余计算。
理解模运算在循环和周期性问题中的作用,对于优化和简化问题具有实际意义。
局部翻转与全局翻转的结合:
先对整个数组进行翻转,再对数组的两部分分别进行翻转。这不仅是对问题解空间的完整覆盖,也体现了对算法步骤合理和有序的安排与设计。
这样的步骤设计有助于理解问题解决的过程,并保证算法在逻辑上的正确性和实现上的简洁性。
DP
参考资料:从0开始最优子结构
能用dp解决的问题的性质:
- 能将大问题拆成几个小问题
- 无后效性:一旦某个状态的子问题计算并记录下来,后续对这个状态的计算结果不会改变,即后续的选择不会影响先前已计算的子问题的最优解。
- 最优子结构
无后效性详解
动态规划(Dynamic Programming,简称 DP)中的无后效性(也叫做无后效性原则,Principle of Optimality)是指,一旦某个状态的子问题计算并记录下来,后续对这个状态的计算结果不会改变,即后续的选择不会影响先前已计算的子问题的最优解。
无后效性可以分为两部分来理解:
子问题独立性:每个子问题的解必须是独立的,不会依赖于其他子问题的具体解,只依赖于子问题本身的输入和子问题的规模。换句话说,子问题一旦解决好,不会因为后续计算对其结果产生影响。
子问题的最优性:如果一个子问题的解已经确认为最优解,那么这个解在后续组合过程中仍然保留最优性,不会因为后续的计算过程改变它的最优性。
为了更好地理解这个概念,举一个常见的动态规划问题——最短路径问题(例如在图中寻找从源点到目标点的最短路径):
假设我们从顶点A到顶点C的最短路径是通过顶点B实现的(即从A到B,再从B到C)。假设现在我们已经知道从A到B的最短路径以及从B到C的最短路径,那么从A到C的最短路径就是从A到B的最短路径加上从B到C的最短路径。
在这里:
- 子问题独立性:路径A到B与路径B到C是独立且最优的。
- 子问题的最优性:路径A到B和路径B到C的最优解不会因为我们组合这些路径而改变。
无后效性是动态规划的核心前提,使得动态规划算法能够通过将问题分解为多个子问题,最终组合其解来解决整体问题。如果没有无后效性,某个子问题的解会因后续选择而发生变化,从而不能保证最终解的正确性和最优性。