王道

栈和队列

知识框架

线性表
- 操作受限
  - 栈
    - 顺序栈
    - 链栈
    - 共享栈
  - 队列
    - 循环队列
    - 链式队列
    - 双端队列
- 推广
  - 数组
    - 一维数组
    - 多维数组：压缩存储，稀疏矩阵

栈的应用(摘自清华大学数据结构c语言版)

进制转换
括号匹配的检验
行编辑程序
迷宫求解
表达式求解:(中缀表达式转后缀表达式,后缀转中缀，从左往右看，后出为左，表达式树的建立)，前缀转中缀，从右往左看，先出为左,后缀表达式的计算,前缀表达式的计算
- 中缀转前后缀：括号法
- 1栈中缀转后缀vs2栈计算中缀$\color{yellow}{\text{p103,t11和课本不一致}}$
  - 弹出表达式的时候会弹出两个数

循环队列长度的计算

取余的理解参考文献1
错误文献，参考文献2
分两种情况，明确Q.rear指向的元素为空，Q.front指向的元素不为空：
Q.rear > Q.front: Q.rear - Q.front ${\textstyle\unicode{x2460}}$ < maxSize
Q.rear < Q.front: maxSize - (Q.front - Q.rear) = maxSize + Q.rear - Q.front < maxSize ${\textstyle\unicode{x2461}}$
${\textstyle\unicode{x2460}}$ = ${\textstyle\unicode{x2461}}$ = (maxSize + Q.rear - Q.front) % maxSize

拓展：循环栈

栈（Stack）

栈的基本概念

栈的定义

栈( Stack）是只允许在一端进行插入或删除操作的线性表。首先栈是一种$\color{red}{\text{线性表}}$，但限定这种线性表只能在某一端进行插入和删除操作。
栈顶(Top)：线性表允许进行插入删除的那一端。
栈底(Bottom)。固定的,不允许进行插入和删除的另一端。
空栈。不含任何元素的空表。
$n$ 个不同元素进栈，出栈元素不同排列的个数为$\dfrac{1}{n+1}C_{2n}^n$($\color{red}{\text{卡特兰数}}$(Catalan))。

栈的基本操作

InitStack ( &S):初始化一个空栈s。
StackEmpty(S):判断一个栈是否为空，若栈s为空则返回true，否则返回false。
Push ( &S, x):进栈，若栈s未满，则将x加入使之成为新栈顶。
Pop ( &S, &x):出栈，若栈s非空，则弹出栈顶元素，并用x返回。
GetTop(S,&x):读栈顶元素，若栈s非空，则用x返回栈顶元素。
DestroyStack (&S):销毁栈，并释放栈s 占用的存储空间(“&”表示引用调用)。

栈的顺序存储结构

顺序栈的实现

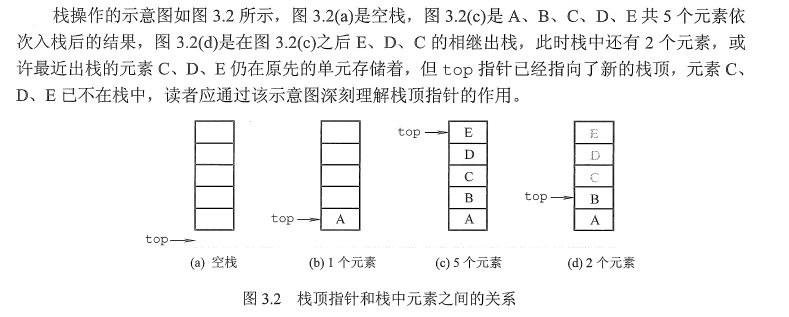
采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top）指示当前栈顶元素的位置。

#define MaxSize 50 //定义栈中元素的最大个数
typedef struct{
  Elentype data [MaxSize];//存放栈中元素
  int top; //栈顶指针
} SqStack ;

栈顶指针:s.top，初始时设置s.top=-1;栈顶元素: s.data[s.top] 。
- 有的教辅可能初始时将(清华c语言版)s.top定义为0，相当于规定top 指向栈顶元素的下一个存储单元。
进栈操作:栈不满时，栈顶指针先加1，再送值到栈顶元素。
出栈操作:栈非空时，先取栈顶元素值，再将栈顶指针减1。
栈空条件: s.top==-1;栈满条件: s.top==MaxSize-1;栈长:s.top+1。

顺序栈的基本运算

初始化

1
2
3

void InitStack(sqStack &S){
  S.top=-l; //初始化栈顶指针
}

判栈空

bool stackEmpty (sqstack s){
  if(s.top==-1) //栈空
    return true;
  else //不空
    return false;
}

进栈

bool Push (SqStack &S,ElemType x){
  if(S.top==MaxSize-1) //栈满,报错
    return false;
  S.data[++S.top]=x; //指针先加1,再入栈
  return true;
}

出栈

bool Pop (SqStack &S,ElemType &x){
  if (S.top==-1)  //栈空,报错
  return false;
  x=S.data [S.top--];//先出栈,指针再减1
  return true;
}

读栈顶元素

bool GetTop (SqStack S，ElemType &x){
  if(s.top==-1)//栈空,报错
  return false;
  x=s.data[s.top] ;//x记录栈顶元素
  return true;
}

共享栈

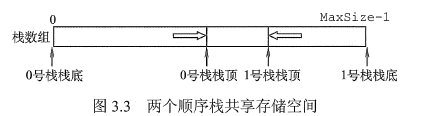
利用栈底位置相对不变的特性，可让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸。

栈的链式存储结构

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的$\color{red}{\text{表头}}$进行的。

typedef struct Linknode{
  ElemType data; //数据域
  struct Linknode *next; //指针域
}*LiStack; //栈类型定义

队列

队列的基本概念

队列的定义

队列(Queue）简称队，也是一种操作受限的线性表，只允许在表的一端进行插入，而在表的另一端进行删除。
队头(Front)。允许删除的一端，又称队首。
队尾(Rear)。允许插入的一端。
空队列。不含任何元素的空表。

队列常见的基本操作

InitQueue ( &Q):初始化队列，构造一个空队列Q。
QueueEmpty(Q):判队列空，若队列Q为空返回true，否则返回false。
EnQueue ( &Q,x):入队，若队列Q未满，将x加入，使之成为新的队尾。
DeQueue (&Q,&x):出队，若队列Q非空，删除队头元素，并用x返回。
GetHead (Q,&x):读队头元素，若队列Q非空，则将队头元素赋值给x。

队列的顺序存储结构

队列的顺序存储

#define MaxSize 50 //定义队列中元素的最大个数
typedef struct{
  ElemType data [Maxsize];//存放队列元素
  int front, rear;//队头指针和队尾指针
} SqQueue;

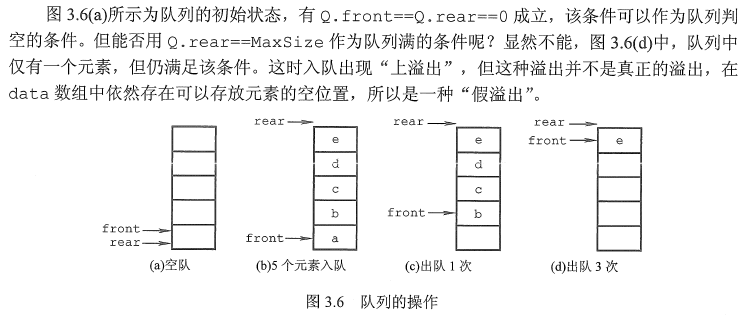
初始状态（队空条件): Q.front==Q.rear==O。
进队操作:队不满时，先送值到队尾元素，再将队尾指针加1。
出队操作:队不空时，先取队头元素值，再将队头指针加1。

循环队列

进和出都是+1
初始时: Q.front=Q.rear=O。
队首指针进1: Q.front=(Q.front+1) %MaxSize。
队尾指针进1: Q.rear=(Q.rear+1)%MaxSize。
队列长度:(Q.rear+MaxSize-Q.front)%Maxsize。
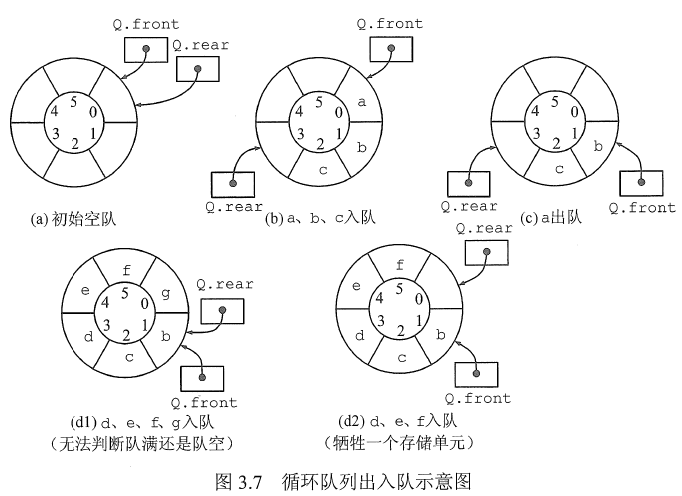
出队入队时:指针都按顺时针方向进1（如图3.7所示)。
为了区分队空还是队满的情况，有三种处理方式:
- 牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是一种较为普遍的做法,约定以“队头指针在队尾指针的下一位置作为队满的标志”
  - 队满条件:(Q.rear+1)%MaxSize==Q.front。
  - 队空条件仍: Q.front==Q.rear。
  - 队列中元素的个数: (Q.rear-Q.front+MaxSize) % MaxSize
- 类型中增设表示元素个数的数据成员。这样，队空的条件为Q.size==0;队满的条件为Q.size==MaxSize。这两种情况都有Q.front==Q.rear。
- 类型中增设tag 数据成员，以区分是队满还是队空。tag 等于0时，若因删除导致Q.front==Q.rear，则为队空; tag等于1时，若因插入导致Q.front==Q.rear，则为队满。

循环队列的操作

初始化

1
2
3

void InitQueue (SqQueue &Q){
  Q.rear=Q.front=0;//初始化队首、队尾指针
}

判队空

bool isEmpty (sqQueue Q){
if(Q.rear==Q.front) return true ;//队空条件
  else return false;
}

入队

bool EnQueue (SqQueue &Q,ElemType x){
  if ((Q.rear+1)%Maxsize==Q.front) return false; //队满则报错Q.
  data[Q.rear]=x;
  Q.rear=(Q.rear+1)%MaxSize;//队尾指针加1取模
  return true;
}

出队

bool DeQueue (SqQueue &Q,ElemType &x){
  if(Q.rear==Q.front) return false; //队空则报错
  x=Q.data [Q.front];
  Q.front=(Q.front+1) % Maxsize; //队头指针加1取模
  return true;
}

队列的链式存储结构

队列的链式存储

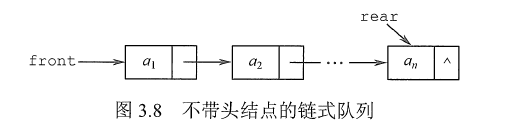
队列的链式表示称为链队列，它实际上是一个同时带有队头指针和队尾指针的单链表。头指针指向队头结点，尾指针指向队尾结点，即单链表的最后一个结点（注意与顺序存储的不同)。

typedef struct {//链式队列结点
  ElemType data;
  struct LinkNode *next;
}LinkNode ;

typedef struct { //链式队列
  LinkNode *front, *rear; //队列的队头和队尾指针
}LinkQueue;

链式队列的基本操作

初始化

void InitQueue(LinkQueue &Q){
  Q.front=Q.rear= (LinkNode* ) malloc(sizeof(LinkNode)) ;//建立头结点
  Q.front->next=NULL;//初始为空
}

判队空

bool IsEmpty(LinkQueue Q){
  if(Q.front==Q.rear) return true;
  else return false;
}

入队

void EnQueue(LinkQueue &Q, ElemType x) {
  LinkNode *s=(LinkNode *)malloc(sizeof(LinkNode) ) ;s->data=x;s->next=NULL;//创建新结点，插入到链尾
  Q.rear->next=s;
  Q.rear=s;
}

出队

bool DeQueue (LinkQueue &Q,ElemType &x){
  if(Q.front--Q.rear) return false; //空队
  LinkNode *p=Q.front->next;
  x=p->data;
  Q.front->next=p->next;
  if(0.rear==p)
    Q.rear=Q.front;//若原队列中只有一个结点，删除后变空
  free(p);
  return true;
}

双端队列

双端队列是指允许两端都可以进行入队和出队操作的队列

栈和队列的应用

栈在括号匹配中的应用

初始设置一个空栈，顺序读入括号。

若是右括号，则或者使置于栈顶的最急迫期待得以消解，或者是不合法的情况（括号序列不匹配，退出程序)。

若是左括号，则作为一个新的更急迫的期待压入栈中，自然使原有的在栈中的所有未消解的期待的急迫性降了一级。算法结束时，栈为空，否则括号序列不匹配。

栈在表达式子求值中的应用

中缀表达式转化为后缀表达式的过程，见本章3.3.6节的习题11的解析，这里不再赘述。

栈在递归中的应用

简单地说，若在一个函数、过程或数据结构的定义中又应用了它自身，则这个函数、过程或数据结构称为是递归定义的，简称递归。
递归必须满足的条件
- 递归表达式（递归体)。
- 边界条件（递归出口)。
可以将递归算法转换为非递归算法，通常需要借助栈来实现这种转换。
递归的效率低下，优点是代码简单，容易理解

队列在层次遍历中的应用

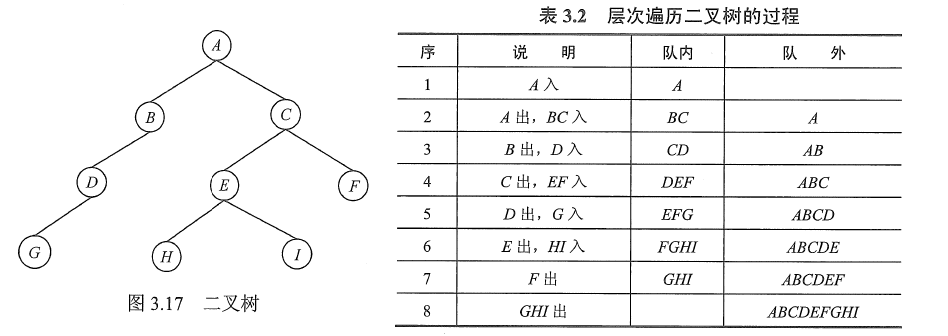
①根结点入队。
②若队空（所有结点都已处理完毕)，则结束遍历;否则重复③操作。
③队列中第一个结点出队，并访问之。若其有左孩子，则将左孩子入队;若其有右孩子，则将右孩子入队，返回②。

队列在计算机系统中的应用

第一个方面是解决主机与外部设备之间$\color{red}{\text{速度不匹配}}$的问题。

对于第一个方面，仅以主机和打印机之间速度不匹配的问题为例做简要说明。主机输出数据给打印机打印，输出数据的速度比打印数据的速度要快得多，由于速度不匹配，若直接把输出的数据送给打印机打印显然是不行的。解决的方法是设置一个打印数据缓冲区，主机把要打印输出的数据依次写入这个缓冲区，写满后就暂停输出，转去做其他的事情。打印机就从缓冲区中按照先进先出的原则依次取出数据并打印，打印完后再向主机发出请求。主机接到请求后再向缓冲区写入打印数据。这样做既保证了打印数据的正确，又使主机提高了效率。由此可见，打印数据缓冲区中所存储的数据就是一个队列。

第二个方面是解决由多用户引起的$\color{red}{\text{资源竞争}}$问题。

对于第二个方面，CPU(即中央处理器，它包括运算器和控制器）资源的竞争就是一个典型的例子。在一个带有多终端的计算机系统上，有多个用户需要CPU各自运行自己的程序，它们分别通过各自的终端向操作系统提出占用CPU的请求。操作系统通常按照每个请求在时间上的先后顺序，把它们排成一个队列，每次把CPU分配给队首请求的用户使用。当相应的程序运行结束或用完规定的时间间隔后，令其出队，再把 CPU分配给新的队首请求的用户使用。这样既能满足每个用户的请求，又使CPU能够正常运行。

特殊矩阵的压缩存储

数组的定义

数组是由n (n>1) 个相同类型的数据元素构成的有限序列，每个数据元素称为一个数组元素，每个元素在n个线性关系中的序号称为该元素的下标，下标的取值范围称为数组的维界。
数组是$\color{red}{\text{线性表的推广}}$。
- 一维数组可视为一个线性表;二维数组可视为其元素也是定长线性表的线性表，以此类推。数组一旦被定义，其维数和维界就不再改变。因此,除结构的初始化和销毁外，数组只会有存取元素和修改元素的操作。

数组的存储结构

逻辑意义上的数组可采用计算机语言中的数组数据类型进行存储，一个数组的所有元素在内存中占用一段连续的存储空间。

矩阵的压缩存储

压缩存储:指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间。其目的是为了节省存储空间。
特殊矩阵:指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。常见的特殊矩阵有对称矩阵、上(下）三角矩阵、对角矩阵等。
特殊矩阵的压缩存储方法:找出特殊矩阵中值相同的矩阵元素的分布规律，把那些呈现规律性分布的、值相同的多个矩阵元素压缩存储到一个存储空间中。

对称矩阵

为此将对称矩阵A[ 1…n ] [ 1…n]存放在一维数组B[ n (n+1)/2]中，即元素$a_{i,j}$(i行j列), 存放在$b_k$中。只存放下三角部分(含主对角）的元素。（由下三角的轮换对称性得到上三角元素的公式）（首项+末项=i，项数=i-1，坐标为j，-1是因为数组从零开始数）
$$
k = \begin{cases}
\dfrac{i(i-1)}{2} + j - 1 & i \geq j (下三角区和主对角线元素) \cr
\dfrac{j(j-1)}{2} + i - 1 & i < j(上三角区元素a_{ij} = a_{ji})
\end{cases}
$$

三角矩阵

下三角矩阵（上三角为常量），i行j列（推导：等差数列求和）
$$
k = \begin{cases}
\dfrac{i(i-1)}{2} + j - 1 & i \geq j (下三角区和主对角线元素) \cr
\dfrac{n(n+1)}{2} & i < j(上三角区元素)
\end{cases}
$$
上三角矩阵，i行j列( 项数=i-1,首项加末项=($\color{green}{\text{n}}$ + $\color{green}{\text{(n-(i-1)+1)}}$) ),第i行的第j个加的偏置为(j-(i-1))，数组是从零开始数的再-1为j-i
$$
k = \begin{cases}
\dfrac{(i-1)(2n-i+2)}{2} + j - i & i \geq j (上三角区和主对角线元素) \cr
\dfrac{n(n+1)}{2} & i < j(下三角区元素)
\end{cases}
$$

三对角矩阵

对角矩阵也称带状矩阵。对于n阶方阵A中的任一元素 $a_{i,j} ，\text{当}\lvert i –j\rvert>1 \text{时，有}a_{i,j}= 0 (1< i, j \text{\textless} n)$，则称为三对角矩阵，如图3.25所示。前$i-1$行共$3(i-1)-1$个元素，$a_{i,j}$是第$i$行第$j-i+2$个元素，$a_{i,j}$是第$2i+j-2$个元素，$k=2i+j-3$

$$
k = 2i + j- 3
$$

已知三对角矩阵中某元素$a_{i,j}$存放于一维数组B的第$k$个位置，则可得$i=\lfloor \dfrac{k+1}{3}+1 \rfloor$,$j=k-2j+3$ (i很好理解，因为可以理解为每行三个元素$i=\lceil \dfrac{k+1}{3} \rceil$)

稀疏矩阵

矩阵中非零元素的个数t，相对矩阵元素的个数s来说非常少，即$s \gg t$的矩阵称为稀疏矩阵。例如，一个矩阵的阶为100×100，该矩阵中只有少于100个非零元素。
稀疏矩阵的三元组既可以采用数组存储，也可以采用十字链表法存储。