凑数
凑数
凑数
凑数
不同数据类型的加减运算
图片详情

解析
图片详情

看到16进制数直接转成10进制也许更好,(从右往左)第一位的权值为0,第二位的权值为16…
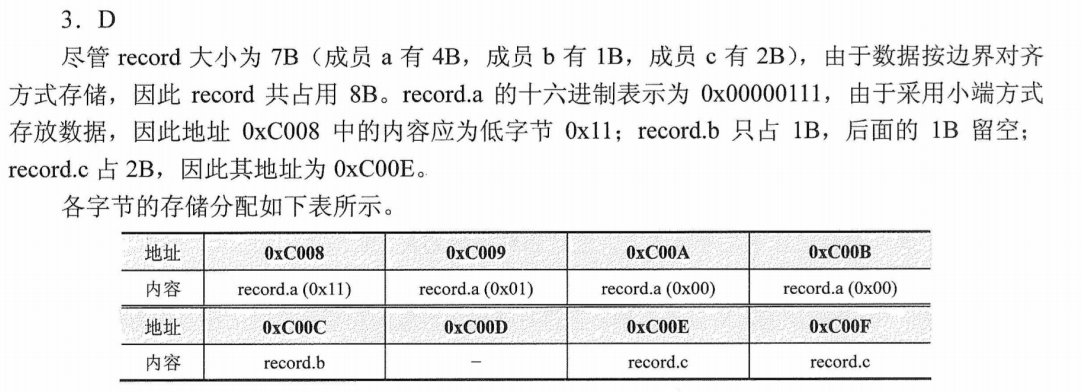
边界对齐
图片详情

解析
图片详情
无符号short转为无符号int
图片详情

解析
图片详情

short的无符号和有符号之间的转换
图片详情

解析
图片详情

这里有个技巧,在补码的语境下,无符号与有符号之间存在互补,二者相加为0
定点小数的表示范围
图片详情

解析
图片详情

少看了一个等于号
定点小数的表示范围
图片详情

解析
图片详情

整数补码的表示
图片详情

解析
图片详情

少看一个等于
定点小数的补码表示
图片详情

解析
图片详情

循环左移,数据寄存器,进位标志寄存器
图片详情

解析
C. 10010101 1
不带进位位的循环左移将最高位进入最低位和标志寄存器C位。
原码的算术移位
图片详情

解析
图片详情

补码的算术移位
图片详情

解析
图片详情

绝对值相反数的补码为其自身的相反数的补码的数
图片详情
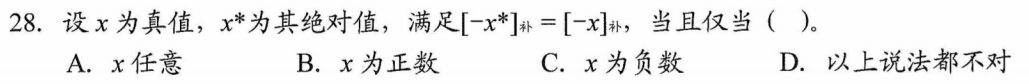
解析
图片详情

题目玩了个文字游戏,是充分必要条件,0不是正数
关于门电路相关的知识
图片详情

解析
图片详情

- 有哪三种判溢方法
- 译码电路,编码电路,移位电路都在什么地方用到了,门电路的实现又是怎么样的
数据的表示综合
图片详情

解析
图片详情

注意正数的补码反码,移码都相同
模4补码的运算
图片详情

解析
图片详情

- 为什么双符号位只在加减法中使用
已知机器数与真值求其表示方法
图片详情

解析
图片详情
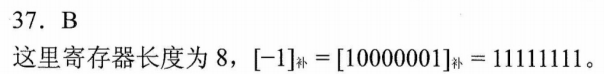
双符号位的判溢条件
图片详情

双符号位的判溢条件
图片详情

解析
图片详情

- 一直推不出来两个负数的溢出为什么是10
符号位进位,最高位进位,判溢条件
图片详情

解析
图片详情

其实举个例子推一遍就出来了
- 结论:判溢条件是最高位和符号位异或
左移时候的溢出
图片详情

解析
图片详情

- 其实考的是补码的表示特点和表示范围
- 单符号位的话,移位的时候符号位不动;看答案的意思,双符号位的话移位的时候符号位也要移动
原码乘法的特点
图片详情

解析
A 先取操作数绝对值相乘,符号位单独处理
原码一位乘法中,符号位与数值位是分开进行运算的。运算结果的数值部分是乘数与被乘数数值位的乘积,符号是乘数与被乘数符号位的异或。
补码一位乘法的加法运算次数和移位次数
图片详情

解析
图片详情
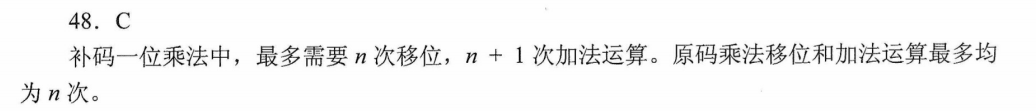
N位补码一位乘,乘积的位数
图片详情

解析
图片详情

原码不恢复余数法
图片详情

解析
52.D
原码不恢复余数法即加减交替法,只在最终余数为负时,才需要恢复余数。
补码除法
图片详情

解析
图片详情

机器数,补码减法
图片详情

解析
图片详情

- 机器数,真值和补码的区别
- 机器数是指一串01序列,其能表示的真值由表示他的方式决定,如(大小端,补码,原码,反码,移码)
小端存储,指令机器码
图片详情

解析
图片详情

有符号数和无符号数的移位
图片详情

解析
图片详情

统一有符号数和无符号数的移位,
- 符号位不变,对数值位移位
- 而无符号数根本没有符号位,所以看起来就像整体移位了一样
2011 考研真题,类型转换与溢出
图片详情

解析
图片详情

- 寄存器5和寄存器6的数值求错
- 寄存器5的错因:无中生有(低四位没有1)
- 寄存器6的错因:有而被去(进位忘了进)
判溢条件:加法器完成加法操作时,若次高位(最高数位)的进位和最高位(符号位)的进位不同,则结果溢出。
定点小数的运算
图片详情
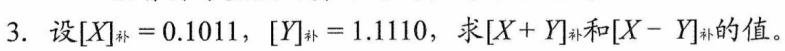
解析
图片详情
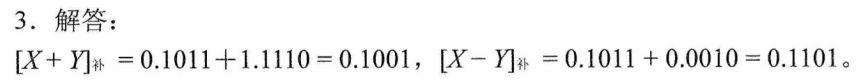
证明题
图片详情
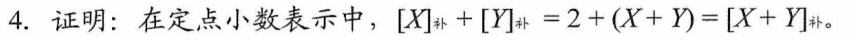
解析
图片详情

- 为什么是2+X
- 可以理解为2-0.多=1.多,这个1.多就是X的补码表示
溢出标志位,符号标志位,进位标志位(OF,SF,CF)
图片详情

解析
图片详情

- 数值位最高位进位那么进位标志位设置为1?
2020真题
图片详情

解析
图片详情

什么是浮点数的溢出?什么情况下发生上溢出?什么情况下发生下溢出?
解析
浮点数的运算结果可能出现以下几种情况:
①阶码上溢出。一个正指数超过了最大允许值时,浮点数发生上溢出(即向$\infty$方向溢出)。若结果是正数,则发生正上溢出(有的机器把值置为+$\infty$);若结果是负数,则发生负上溢出(有的机器把值置为-$\infty$)。这种情况为软件故障,通常要引入溢出故障处理程序来处理。
②阶码下溢出。一个负指数比最小允许值还小时,浮点数发生下溢出。一般机器把下溢出时的值置为0(+0或-0)。不发生溢出故障。
${\textstyle\unicode{x2462}}$ 尾数溢出。当尾数最高有双过.月慰不出为止。此时,只要阶码不发生上溢出,浮点数数右移一位,阶码加1,直到尾数不溢出为止。此时,只要阶码不发生上溢出,浮点数就不会溢出。
④非规格化尾数。当数值部分高位不是一个有效值时(如原码时为О或补码时与符号位相同),尾数为非规格化形式。此时,进行“左规”操作:尾数左移一位,阶码减1,直到尾数为规格化形式为止。
求32位二进制补码,无符号,IEEE 754单精度浮点数对应的真值
图片详情

解析
图片详情

注意IEEE 754标准中的移码是减去127而不是128
给定浮点数求机器数
图片详情

解析
图片详情

$\blacktriangleright$(三位阶码怎么表示的出来十进制的10??)
不同基值下的浮点数对比
图片详情

解析
图片详情

- 求最大正数时,注意符号位占据了一位
- 注意最小正数阶码要负的最小
$\blacktriangleright$(基值为16的浮点数的对阶操作)
浮点数的相加相减
图片详情

解析
图片详情

- $\blacktriangleright$(浮点数结果的相加等不等于相加的结果)
- 需要注意每一个位置的位数
两个规格化浮点数进行加减法运算,最后对结果规格化时,能否确定需要右规的次数?能否确定需要左规的次数?
解析
两个n位数的加减运算,其和/差最多为n+1位,因此有可能需要右规,但右规最多一次。由于异号数相加或同号数相减,其和/差的最少位数无法确定,因此左规的次数也无法确定,但最多不会超过尾数的字长n位次。
IEEE 754单精度浮点数机器数的边界值
图片详情

解析
图片详情

- 注意浮点数阶码是减127
2017年真题 IEEE754 标准
图片详情

解析
图片详情

- $\mho$(IEEE 754尾数舍入到底是怎么回事???)
2011统考真题:IEEE 754单精度浮点数的加减
图片详情

解析
图片详情
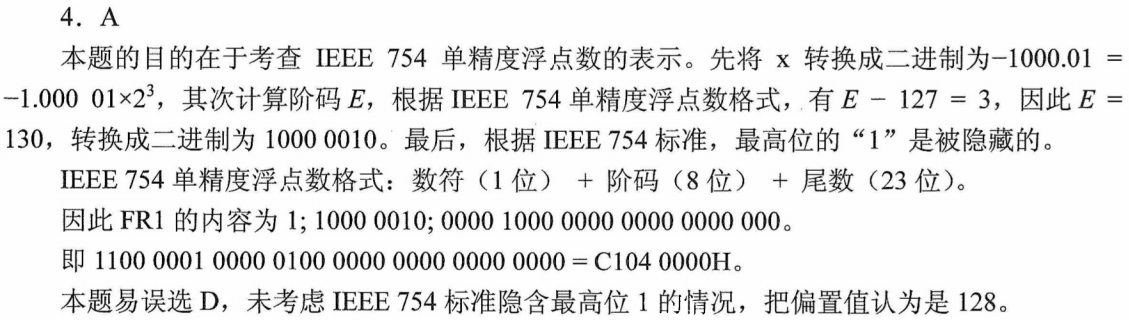
2012统考真题:IEEE 754单精度浮点数的最值
图片详情

解析
图片详情

浮点数的规格化
图片详情

解析
图片详情

- $\mho$(为什么只能左移不能右移)
原码表示尾数的浮点数机
图片详情

解析
图片详情

- 不要和补码搞混了
- 和尾数补码表示法不同,补码表示中负数必须是1.0xxx,原码表示尾数的话负数必须是1.1xxx
基数为8的补码规格化浮点数
图片详情

解析
图片详情

对阶操作的描述
图片详情

解析
图片详情

规格化浮点数的原因
图片详情

解析
图片详情

增加数据的表示精度
下溢的定义
图片详情

解析
图片详情

基数为4,尾数用原码表示的规格化数
图片详情

解析
图片详情

二进制浮点数运算规格化结果
图片详情

解析
图片详情

关于舍入的说法
图片详情

解析
图片详情

- 舍入是浮点数的概念
IEEE 754最小规格化正数,2018真题
图片详情

解析
图片详情

加法器中进位信号的形成
图片详情
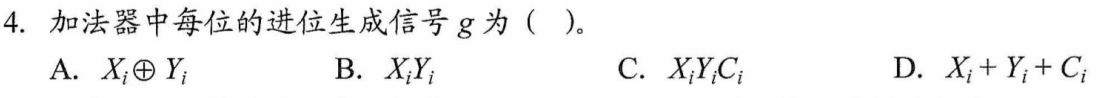
解析
图片详情
运算器的组成部件
图片详情

解析
图片详情

- $\mho$(不太懂)
进位的逻辑表达式
图片详情
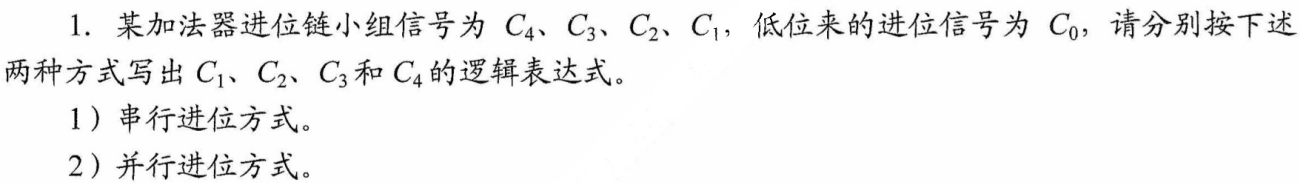
解析
图片详情

- $\mho$(不太懂)