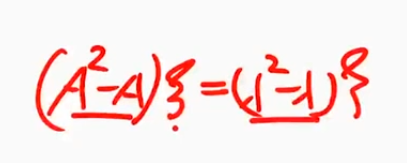ednow

0%

习题-基础30讲-线性代数-ch5-特征值与特征向量

发表于 更新于
本文字数： 842 阅读时长 ≈ 1 分钟

凑数

凑数

凑数

凑数

例2.5.1
解析
  • 解题技巧：由于行列式为0，所以秩最多是$n-1$
  • 注：不能有0解，不同时为0
总结
题型错因教训视频讲解
true
注2真题
解析
  • 技巧：(提出法)提出$\lambda+2$
  • 用试根法
  • 总结
    题型错因教训视频讲解
    true
例2.5.4
解析
  • 原理
  • 只能是范围，不能是确实是
总结
题型错因教训视频讲解
true
例2.5.5
解析
  • 证明题，思路就是用定义法
总结
题型错因教训视频讲解
true
例2.5.8
解析
  • 迹刚好是对角线元素之和
  • 3阶伴随刚好为任意矩阵的
总结
题型错因教训视频讲解
true
例2.5.10
解析
  • 能够相似对角化的条件
  • B:有三个不同的$\lambda$必然有三个不同的$\xi$可以相似对角化（使用条件 ${\textstyle\unicode{x2462}}$ ）
  • C:$\bigstar$ $\bigstar$ $\bigstar$ 秩为1的话有技巧，有n-1个0，然后主对角线的和是另外一个特征值（使用条件 ${\textstyle\unicode{x2461}}$ ）($\blacktriangleright$(这个算法的依据是什么))
总结
题型错因教训视频讲解
true
例2.5.12
解析
  • 相似矩阵的传递性
总结
题型错因教训视频讲解
true
例2.6.3

改写为如下

解析
总结
题型错因教训视频讲解
true
例2.5.16
解析
  • 证明结论：实对称矩阵$\mathbf{A}$的属于不同特征值的特征向量相互正交(证明见例2.5.16).
  • 穿脱原则
总结
题型错因教训视频讲解
true
例2.5.18
解析
  • 两个矩阵相似，迹相同，行列式相同
总结
题型错因教训视频讲解
true
例2.5.20
解析
  • 逆矩阵的特征值就是原矩阵的特征值
总结
题型错因教训视频讲解
true
例2.5.21
解析
  • 反求矩阵的第一种方法
总结
题型错因教训视频讲解
true
习2.5.11
解析
  • 反求矩阵的第二种方法
  • 先讨论能不能相似对角化
    • 讨论的对象中有参数，但是特征方程可能不含有参数
总结
题型错因教训视频讲解
true
例2.5.22
解析
  • 反求矩阵的第三种方法
总结
题型错因教训视频讲解
true