凑数
凑数
凑数
凑数
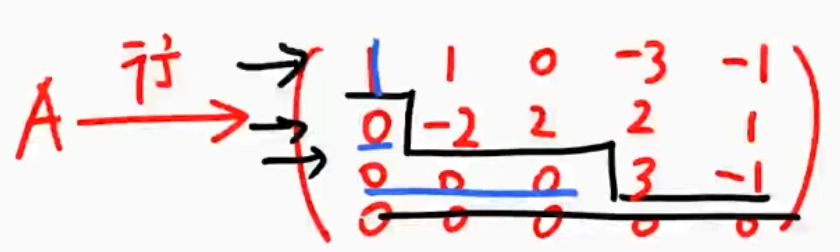
例2.4.1
解析
- 按照线性方程组的步骤求解齐次线性方程组
- 不要按照书本的答案来写,按照这个来写(这也是之前上课学的)
行阶梯型(消元)
- 若有0行,全在下方
- 从行上看,自左起出现连续0的个数自上而下严格单增
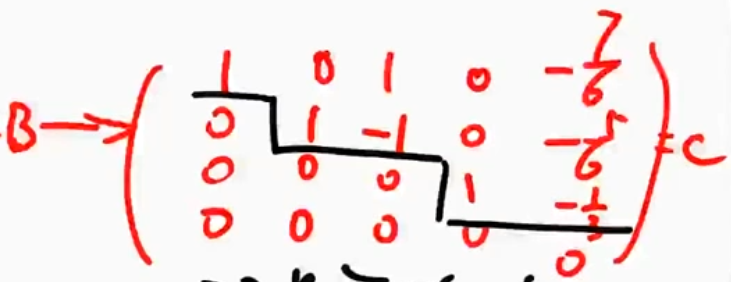
行最简阶梯型(代入)
- 若有0行,全在下方
- 从行上看,自左起出现连续0的个数自上而下严格单增
- 台脚元素为1
- 台脚正上方元素全为0
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.2
解析
- 先检查是否有解
- 求非齐次线性方程组
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.3
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
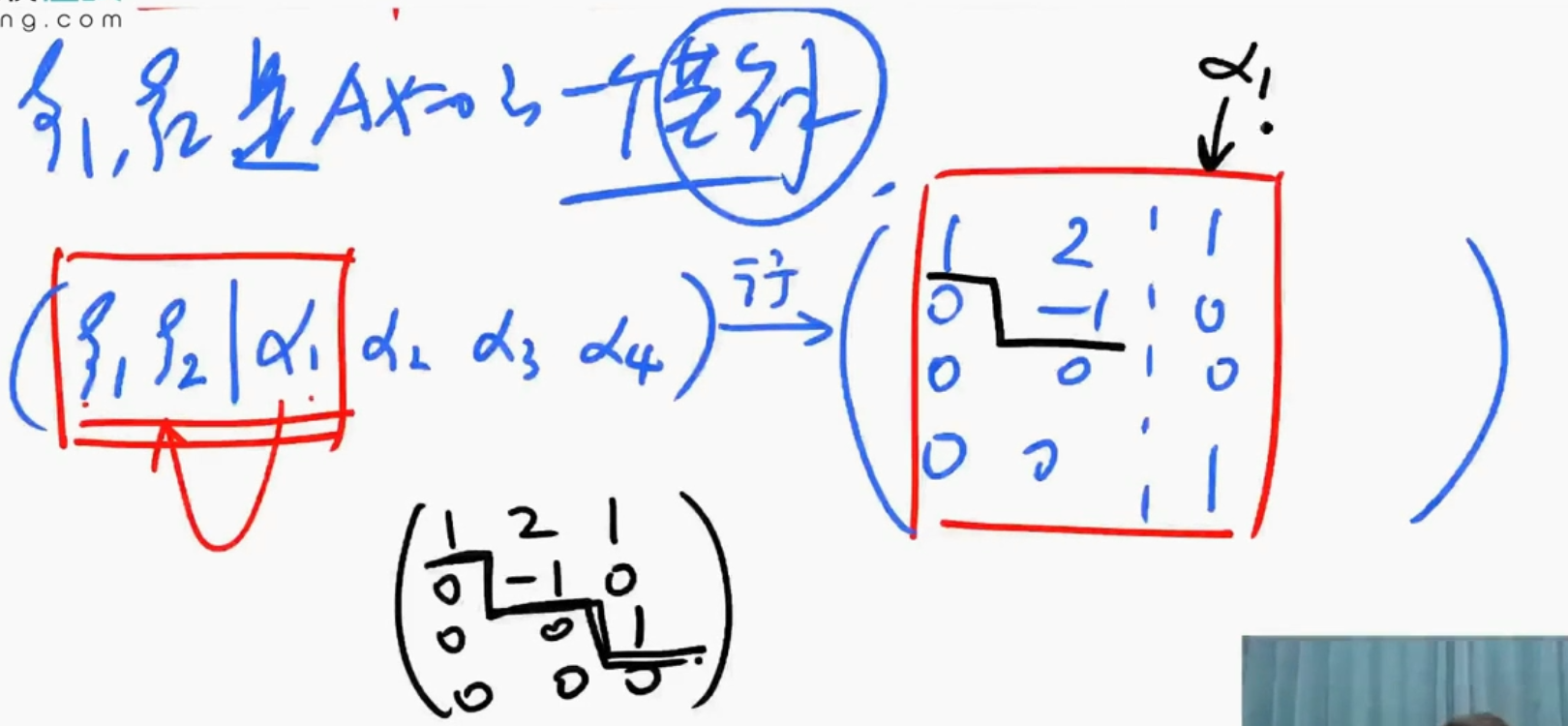
例2.4.5
解析
- 抽象型有解问题
- $\mho$(没怎么听懂)
- A:$\mathbf{A}$线性无关和无关($r(\mathbf{A}) \leq n$)(列满秩)($\mathbf{A}x=0$有零解或无穷多解),和$\mathbf{\beta}$能不能被$\mathbf{A}$线性表示($r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta})$)($\mathbf{A}x=\mathbf{\beta}$有没有解)没有关系
- $\mathbf{A}x=\mathbf{\beta}$有唯一解 $\implies r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta}) = n \implies \mathbf{A}x=0$ 只有零解
- $\mathbf{A}x=\mathbf{\beta}$有无穷多解 $\implies r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta}) < n \implies \mathbf{A}x=0$ 有非零解,即有无穷多解
- A行满秩 $\implies r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta})$
- $\bigstar$(行满秩和列满秩的区别是什么)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.7
解析
- 写成增广矩阵的方式求解
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.8
解析
- 基础解系的题目,(线性无关)算行列式。
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.9
解析
- 系数矩阵列向量与解的关系
- 缺的补0
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.11
解析
- 令其基础解系相等
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.12
解析
- 2的解必为1的解
- 只要1的解满足2即可
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
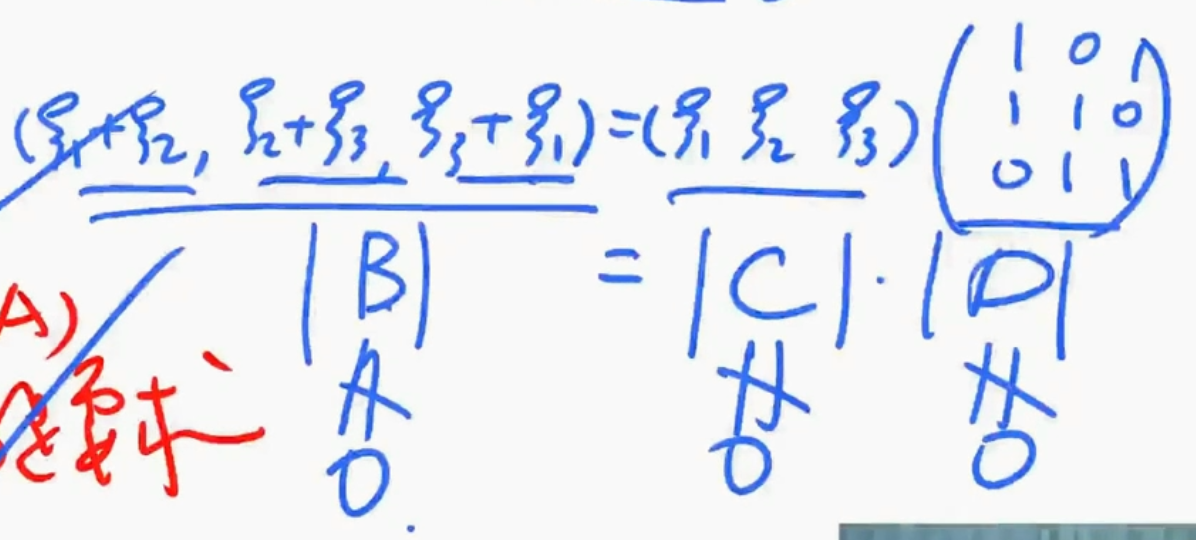
习2。4.7
解析
- $\bigstar$ 极为重要的经典题目
- 设$A_{m\times n}$, 则$r(\mathbf{A})=r(\mathbf{A}^T)=r(\mathbf{A}\mathbf{A}^T)=r(\mathbf{A}^T\mathbf{A})$
- 15个关于秩的关系式
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |