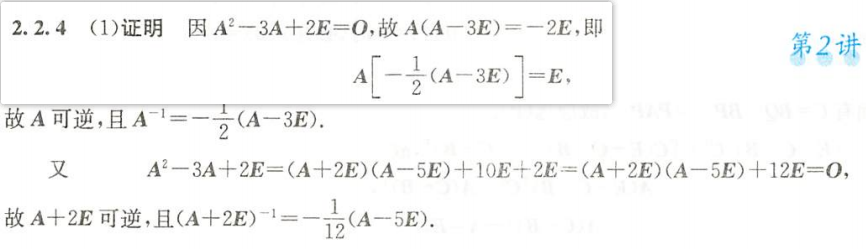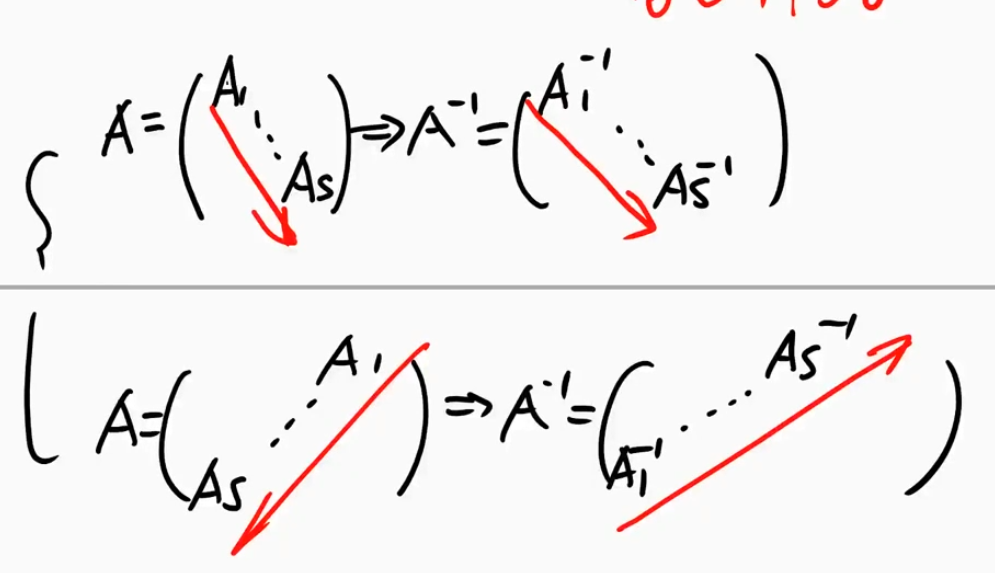凑数
凑数
凑数
凑数
例2.2.1
解析
- 行呈比例,可以反拆
- 运用结合律
- 拓展:$A^n=[tr(A)]^{n-1}A$
总结
例2.2.2
解析
总结
例2.2.3
解析
- $\mathbf{A}^n$的运算,一共三种考题,强化拓展至5种
- $r(\mathbf{A})=1$ 例2.2.1
- 算$\mathbf{A}^2,\mathbf{A}^3$ 归纳出结果 例2.2.2
- $\mathbf{A}^n=(\mathbf{B}+\mathbf{C})^n=\cdots(\text{用展开式,前提可交换,其中有一个是}\mathbf{E})$
- 初等阵
- 相似对角化理论
- 跟幂函数的求导类似,只有前几项是有值的,后面都是0
稀疏矩阵中可能有门道
错因:算$\mathbf{A}^3$时用$\mathbf{A}^2 \times \mathbf{A}^2$来算了,实际上应该是$\mathbf{A}^2 \times \mathbf{A}^1$
总结
例2.2.4
解析
- $\bigstar$
- 列方程
- 解:用$\color{red}{\text{矩阵初等变化}}$,或者高中的高斯消元,代入法
点乘为0就是正交,正交向量不需要转置
总结
例2.2.5
解析
总结
例2.2.6
解析
$\bigstar$
- 对称矩阵:$\mathbf{A}^T=\mathbf{A}$
- 证明正交矩阵,用定义法$\mathbf{A}^T\mathbf{A}=\mathbf{E}$
总结
例2.2.7
解析
- 用伴随矩阵求逆矩阵
- 二阶的逆矩阵背下来,口诀:主对调,副变号
总结
例2.2.8
解析
总结
例2.2.9
解析
总结
例2.2.10
解析
总结
例2.2.10
解析
- 运用 A的伴随的重要的秩的值,例2.3.12的结论
总结
例2.2.11
解析
总结
例2.2.13
解析
- 证明可逆:行列式不为0
- 求逆:列方程
- 结论记忆的方法口诀:
- 主对角线三角:主对角线:求逆,副对角线:左乘同行,右乘同列,添负号
- 副对角线三角:副对角线:换位置求逆,副对角线:左乘同行,右乘同列,添负号
对角阵的逆,对角线元素求倒数

总结
例2.2.19
解析
总结
例2.2.20
解析
- $\blacktriangleright$(只要等于$\mathbf{E}$所有的矩阵都可逆?为什么?)
总结
例2.2.23
图片详情

解析
- 对$n$阶矩阵$\mathbf{A}$进行初等行变换,相当于矩阵$\mathbf{A}$左乘相应的初等矩阵.同样,对$\mathbf{A}$进行初等列变换,相当于矩阵A右乘相应的初等矩阵.
- 学校教的方法解这题好像更好(这个课程后面好像有讲)?
图片详情

$\color{red}{\text{Q}}$:这个好像要用到向量方程组的知识了,后面再来看看?第二讲09视频讲过这道题,但是没有扩展下面的知识点
求满足条件的全部矩阵p

总结
习2.2.5
解析
总结
习2.2.1:求矩阵的幂
图片详情

解析
图片详情

写成两个矩阵的乘积
题目tag详情
总结
用定义法证明可逆
图片详情

解析
图片详情

如果题目要求两个变量可逆,但是一步不能到位的话可以一个变量一个变量的求
题目tag详情
总结