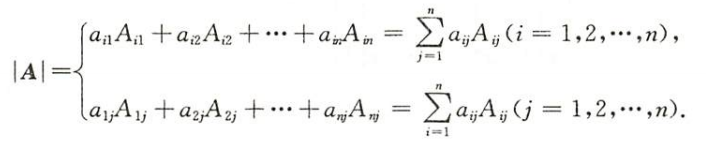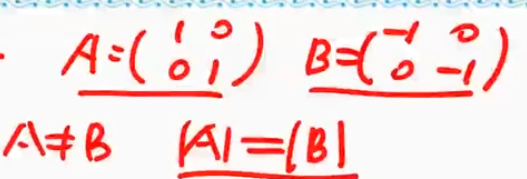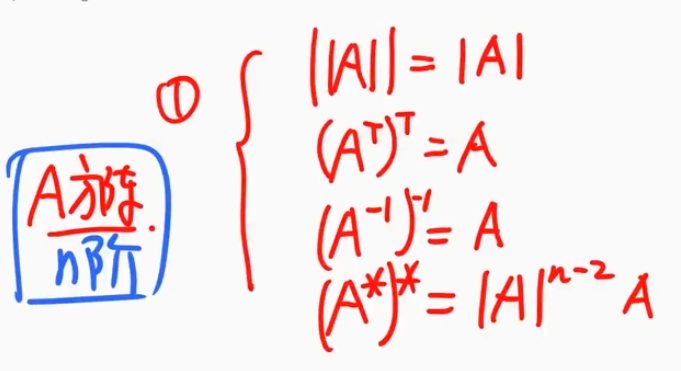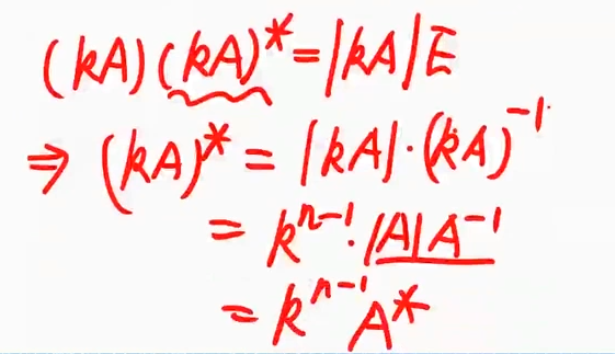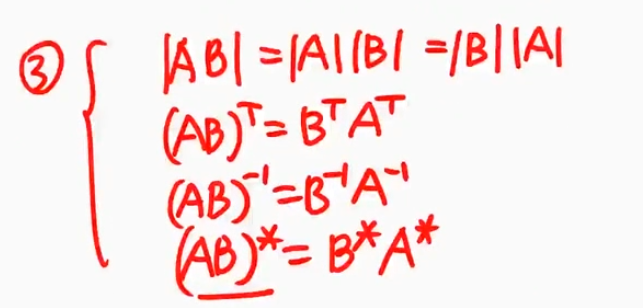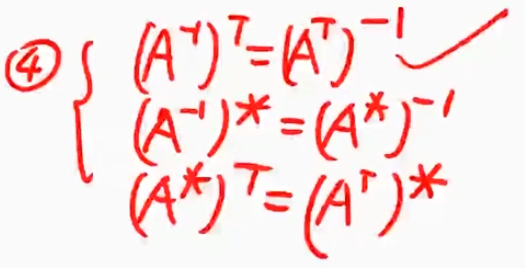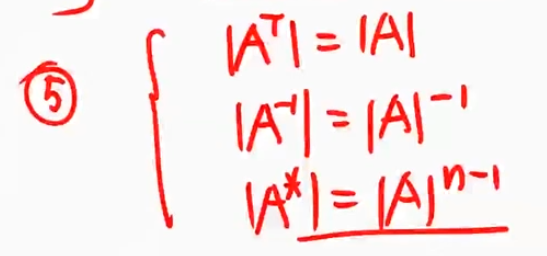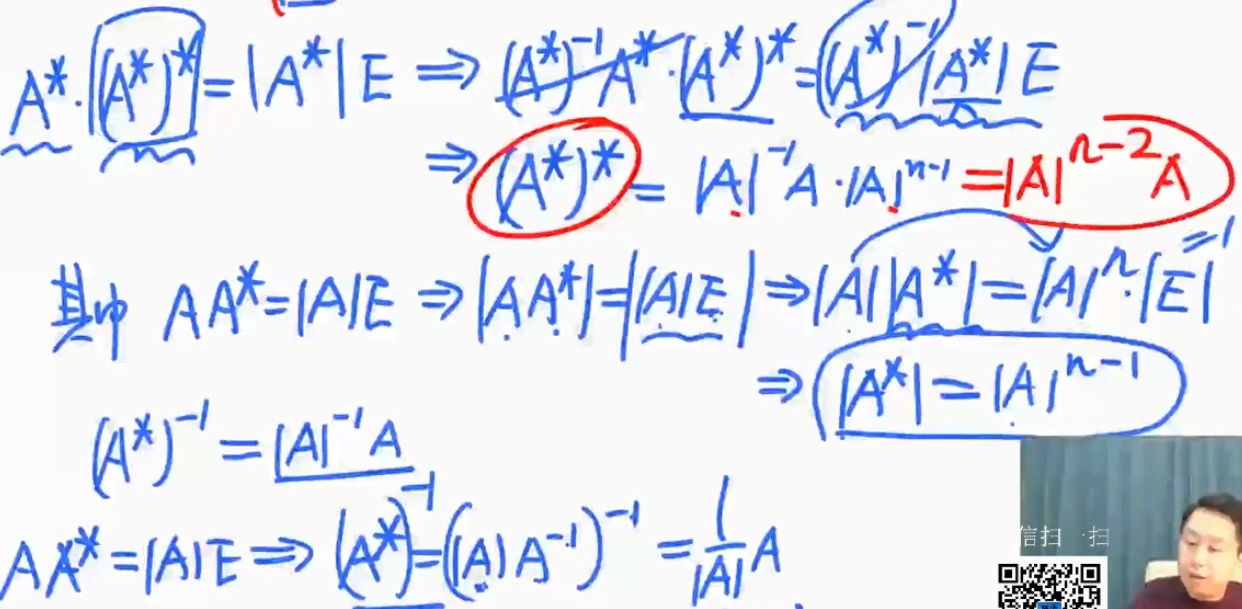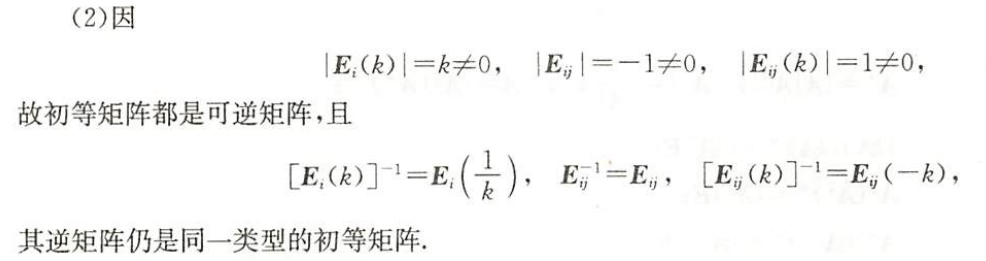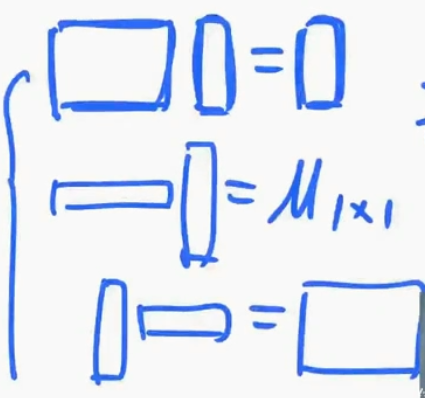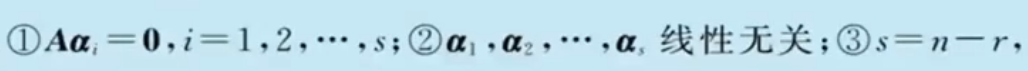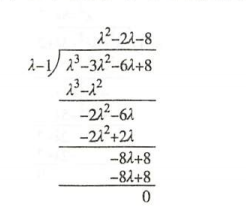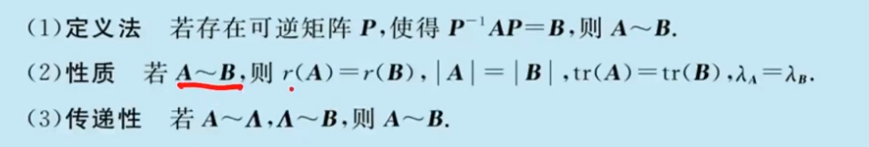zy2022-线性代数
行列式
p295
5分
只有方阵才能谈行列式
行列式的定义与性质
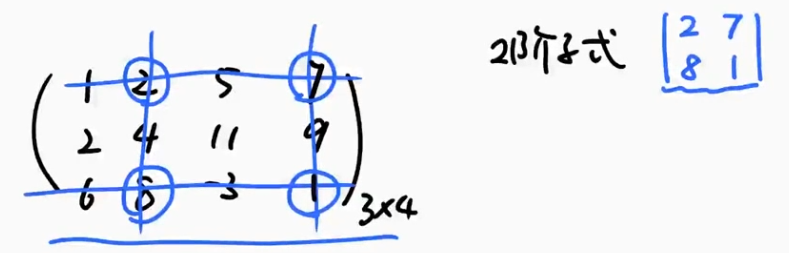
$a_{ij}$ i代表行号,j代表列号
主对角线,左上到右下;副对角线,右上到左下
行列式用字母$D$表示
本质定义(第一种定义)
- 2阶行列式是由两个2维向量(行向量)组成的,其(运算规则的)结果为以这两个向量为邻边的平行四边形的面积
- 3阶行列式其(运算规则的)结果为以这三个向量为邻边的平行六面体的体积.
- n阶行列式是由n个n维向量其(运算规则的)结果为以这n个向量为邻边的n维图形的体积.
- 由此看来,一个重要观点出现了:读者一开始,就应该把行列式看作是由若干个向量拼成的,并且要把这些向量作运算.
- 行列式线性无关,可以理解为行向量组成的图形面积不为0
- 行列式研究两个向量线性相关的一种工具
- 行列式算出来到底是几不重要,等不等于0才重要
性质
性质1 行列互换,其值不变,即 $|A|=|A^T|$.
性质2 行列式中某行(列)元素全为零,则行列式为零.(面积为0)
性质3 行列式中某行(列)元素有公因子k(k $\neq$ 0),则k可提到行列式外面
- 注意只乘进某一行去
- 用面积理解也好理解
- 倍乘
$$
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
ka_{i1} & ka_{i2} & \cdots & ka_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
= k
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
a_{i1} & a_{i2} & \cdots & a_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
$$
性质4 行列式中某行(列)元素均是两个元素之和,则可拆成两个行列式之和,
- 注意是$\color{red}{\text{单}}$行可加性
$$
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
a_{i1} + b_{i1} & a_{i2} + b_{i2} & \cdots & a_{in} + b_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
=
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
a_{i1} & a_{i2} & \cdots & a_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
+
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
b_{i1} & b_{i2} & \cdots & b_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
$$
性质5 行列式中两行(列)互换,行列式的值反号.
- 互换性质
性质6 行列式中的两行(列)元素相等或对应成比例,则行列式为零.
- 性质7和性质2可以推导性质6
性质7 行列式中某行(列)的k倍加到另一行(列),行列式的值不变.
- 倍加
初等变换
- 互换
- 倍乘
- 倍加
逆序数法定义(第二种定义)
- 可以用来检验
排列和逆序
排列:由n个数$1,2,\cdots,n$组成的一个有序数组称为一个n级排列,如23145是一个5级排列,41352也是一个5级排列.n级排列共有n!个.
逆序:一个n级排列$i_1i_2\cdots i_s\cdots i_t \cdots i_n$。中,若$i_s>i_t$,且$i_s$排在$i_t$,前面,则称这两个数构成一个逆序.
逆序数:一个排列中,逆序的总数称为该排列的逆序数,记作 $\tau(i_1i_2\cdots i_n)$,如$\tau$(231546)=3,$\tau$(621534)=8.由小到大顺排的排列称为自然排序,如12345,显然,自然排序的逆序数为0.
奇排列和偶排列:排列的逆序数为奇数时,该排列称为奇排列;排列的逆序数为偶数时,该排列称为偶排列.
n阶行列式的定义
取不同行不同列的乘积,行下标顺排,故为$n!$项和。当列下标为奇排列时,应附加负号;当列下标为偶排列时,应附加正号.
- 用来求给定展开项的正负号
展开定理(第三种定义)
$\bigstar$ $\bigstar$ $\bigstar$
余子式
$$\text{在}n\text{阶行列式中,去掉元素}a_{ij}\text{所在的第i行、第j列元素,}$$
$$\text{由剩下的元素按原来的位置与顺序组成的}n-1\text{阶行列式称为元素}a_{ij}\text{的余子式,记作}M_{ij}$$
代数余子式
$\bigstar$ $\bigstar$ $\bigstar$
$$
\text{余子式}M_{ij}\text{乘}(-1)^{i+j}\text{后称为}a_{ij}\text{的代数余子式,记作}A_{ij}\text{,即}
$$
$$
A_{ij}=(-1)^{i+j}M_{ij}
$$
行列式按某一行(列)展开的展开公式
行列式的值等于行列式的某行(列)元素分别乘其相应的代数余子式后再求和,即
但行列式的某行(列)元素分别乘另一行(列)元素的代数余子式后再求和,结果为零,即
几个重要的行列式
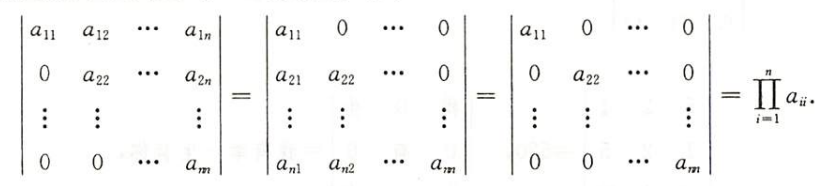
主对角线行列式
副对角线行列式
- 系数可以用逆序来理解
拉普拉斯展开式
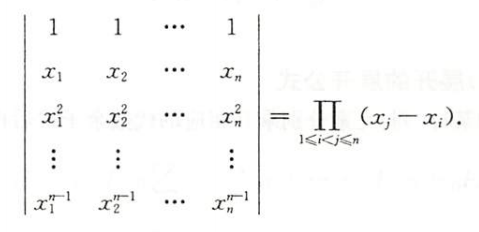
范德蒙德行列式
下标大的要把下标比他小的都减一遍再相乘
$\bigstar$ 行列式的计算
$\color{red}{\text{一句话总结}}$:${\textstyle\unicode{x2460}}$ 初等行变化,化成基本型,${\textstyle\unicode{x2461}}$递推
直接展开
- 0元素很多的情况
- 阶数不高的情况
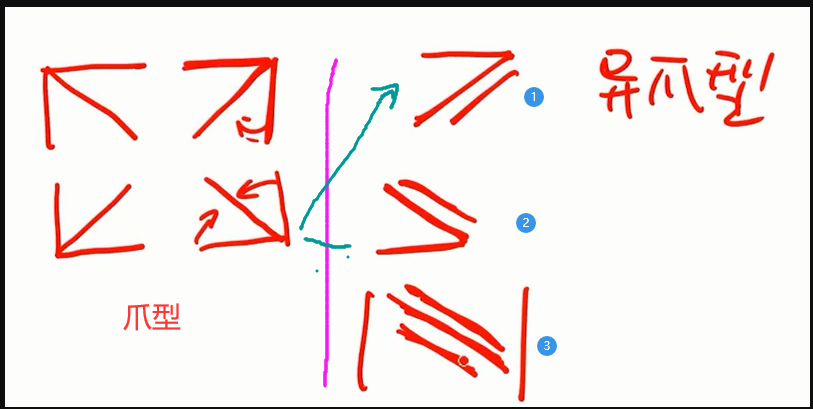
爪形
- 斜爪消平爪:依次提出斜爪上的值(倍乘性质),从第二行开始每一行依次去减第一行,就会变成主对角线行列式
异爪形
- 阶数低,直接展开:第${\textstyle\unicode{x2462}}$ 种 从最下面那一行开始展开比较好
- 阶数高,递推
- $\text{建立} D_n \text{与} D_{n-1} \text{的关系} \implies D_n $
- 找的$D_{n-1}$满足分布相同只是阶数降了一阶
行(列)和相等
- 加到第一行(列),提出去,在做初等变换(用第一行(列)去减下面的每一行)变成主对角行列式
消零化基本形
拉普拉斯展开:交换行列变成拉普拉斯展开
范德蒙德行列式
爪型vs异爪型
基本型指的是4个重要的行列式
具体型
化为基本型
递推法
行列式表示的函数和方程
抽象型
用性质
用公式$|AB|=|A||B|$
公式证明的参考文献
余子式与代数余子式的计算
$$
a_{ij}\text{的}A_{ij}(\text{代数余子式})\text{与}i,j(\text{的位置})\text{有关,与}a_{ij}\text{的大小无关}
$$
矩阵
pp327(进度)
p314
注:2021考研实际线代大概分数为12分
矩阵的定义及其基本运算
- 矩阵的加减乘除
- 表达系统信息.
- 重要观点
- 矩阵也是由若干行(列)向量拼成的
- 矩阵不能运算,但是其若干行(列)向量之间存在着某种联系
秩:矩阵秩的本质就是组成该矩阵的线性无关的向量的个数.
设A是m×n矩阵,A中最高阶非零子式的阶数称为矩阵A的秩,记为r(A).
也可以这样定义;若存在k阶子式不为零,而任意k十1阶子式(如果有的话)全为零,则r(A)=k,且
$$
r(A_{n\times n})(\text{满秩})=n \iff |A| \neq 0 \iff A\text{可逆}
$$
n阶子式的概念
矩阵的四大运算
- 行列式
- 转置
- 逆
- 伴随
$\color{red}{\text{Q}}$:如何化成单位矩阵
$\color{red}{\text{A}}$:如下图,注意最好不要一开始用第一行化不然的话,容易化成副对角矩阵,还要交换n-1次(消第一列的话还是会消成主对角阵)
图片详情
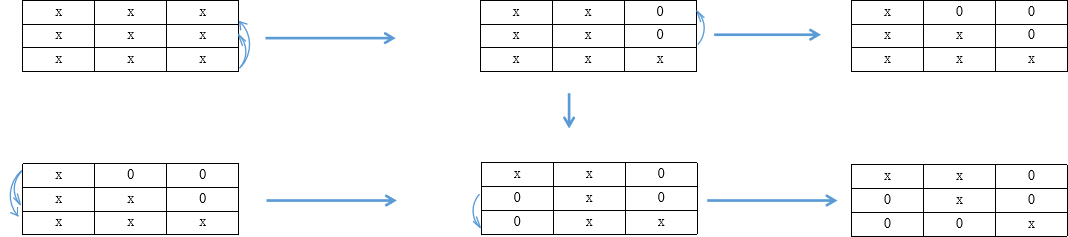
证明题万能思路:要么是考定义,要么是考运算(初级阶段
定义
同型矩阵:两个矩阵,行数和列数相等
方阵:对于一个矩阵,其行数和列数相等
几种重要的矩阵
对称矩阵:关于主对角线对称, $\mathbf{A}^T=\mathbf{A}$
$\bigstar$ 正交矩阵:$\mathbf{A}\mathbf{A}^T=\mathbf{A}^T\mathbf{A}=\mathbf{E}$,由规范正交基组成
分块矩阵:子矩阵
对角矩阵:非主对角元素均为零的矩阵称为对角矩阵.
基本运算
加法运算和数乘运算统称为矩阵的线性运算,满足下列运算规律:
${\textstyle\unicode{x2460}}$ 交换律A+B=B+A;
${\textstyle\unicode{x2461}}$ 结合律(A+B)+C=A+(B+C);
${\textstyle\unicode{x2462}}$ 分配律k(A+B)=kA+kB,(k+l)A=kA+lA;
${\textstyle\unicode{x2463}}$ 数和矩阵相乘的结合律k(lA)=(kl)A=l(kA).
其中,A,B,C是同型矩阵,k,l是任意常数.
当n阶方阵A计算行列式时,记成|A|.
注意
- $|kA|=k^n|A|\neq k|A|$
- 一般$|A+B| \neq |A|+|B|$:($\mathbf{A}+\mathbf{B}=\mathbf{0}$,但$\mathbf{A},\mathbf{B}$都不是$\mathbf{0}$)
- $A \neq \mathbf{0} \nRightarrow |A|\neq 0$
- $A \neq B\nRightarrow |A|\neq |B|$
相等
同型矩阵,且对应元素相同
加法
同型矩阵可加
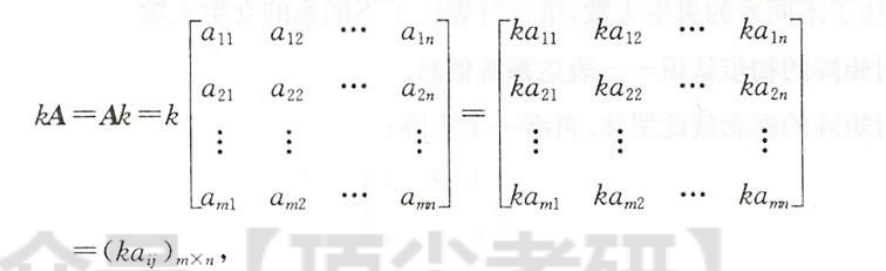
数乘矩阵
每一个元素都要乘
矩阵乘法
满足的规律
- 结合律
- 分配律
- 数乘与矩阵乘积的结合律
- 矩阵的乘法一般不满足交换律
矩阵乘法不满足交换律:但是当矩阵时一阶矩阵的时候可以提到外面去
转置矩阵
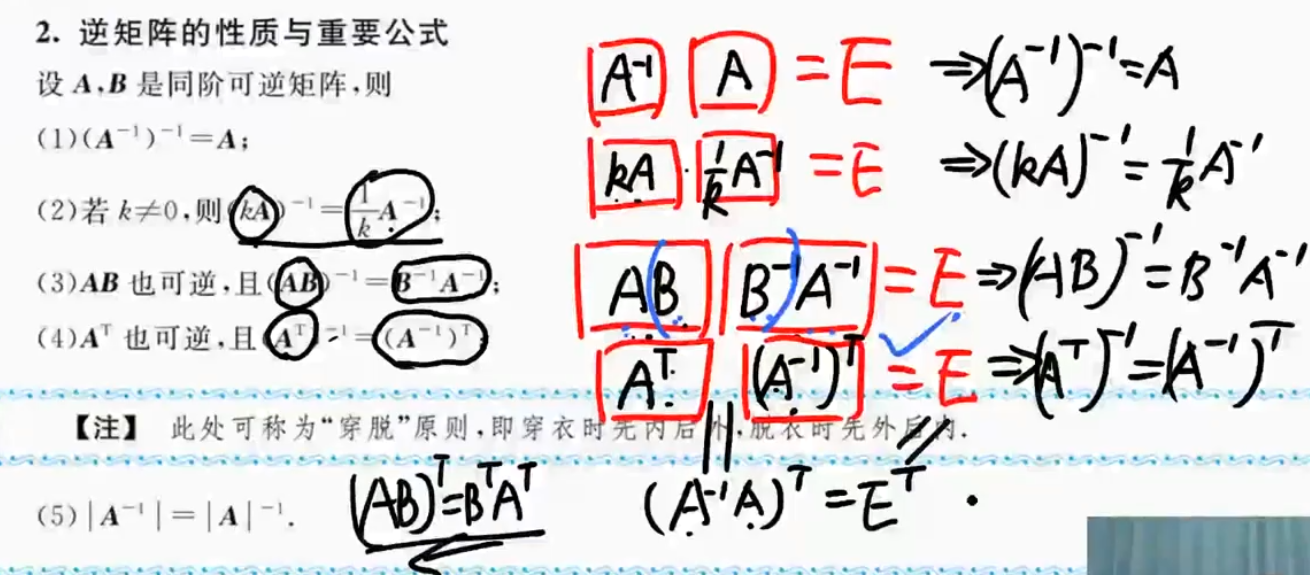
转置矩阵的运算规律
- $(A^T)^T=A$
- $(kA)^T=kA^T$
- $(A+B)^T = A^T+ B^T$
- $(AB)^T=B^TA^T$
- $\text{当}m=n时,|A^T|=|A|$
向量的内积与正交
$\alpha\text{与}\beta$的内积记为$(\alpha,\beta)$
默认$\alpha$是列向量,线代里面向量不打箭头
正交:当$\alpha^T\beta=0,\text{称向量}\alpha \cdot \beta\text{是正交向量}$
模:L2正则
标准正交向量组:任一向量的模为1,任两向量的内积为0
施密特正交化
施密特正交化的方法
施密特正交化的时候对求出来的正交向量标准化的时候,可以直接让分母消失,再算(其余就需要用公式了,只有最后标准化的时候可以投机)
矩阵的幂
$\mathbf{A}\text{是一个方阵}\overbrace{AA\cdots A}^{m\text{个}}\text{称为}\mathbf{A}\text{的}m\text{次幂}$
可以运用多项式
求矩阵幂的方法:矩阵乘法的结合律,求一次再用结合律,化成$\mathbf{E}+\mathbf{A}$
拆成两个矩阵(列*行)的乘积,中间用结合律为常数
多写几次找规律(最万能)
矩阵的幂的性质
- 主对角线元素为零的上三角矩阵$\mathbf{B}$,有$\mathbf{B}^n=\mathbf{O}$
方阵乘积的行列式
设$\mathbf{A}\mathbf{B}$是同阶方阵,则$|AB|=|A||B|$
复合运算(三大运算,7组重要的公式)
${\textstyle\unicode{x2460}}$ A是方阵,两重相同的运算结果
${\textstyle\unicode{x2461}}$ 数乘
- 最后一项的推导($\text{狗}\text{狗}^\star= |狗|\mathbf{E}$)
${\textstyle\unicode{x2462}}$ 穿脱原则
- 最后一项的推导
${\textstyle\unicode{x2463}}$ 三大运算,任何两个运算交换,结果不变
${\textstyle\unicode{x2464}}$ 三大运算的行列式
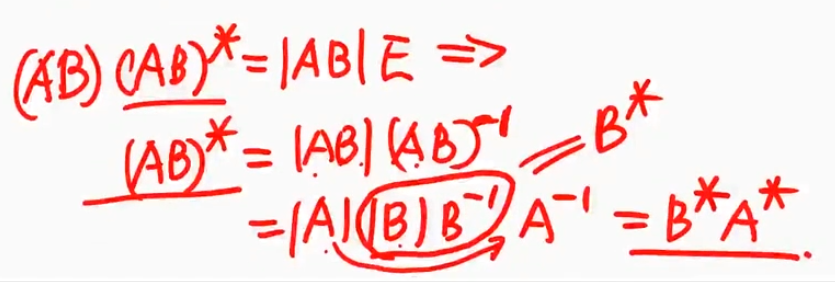
伴随矩阵行列式的推导
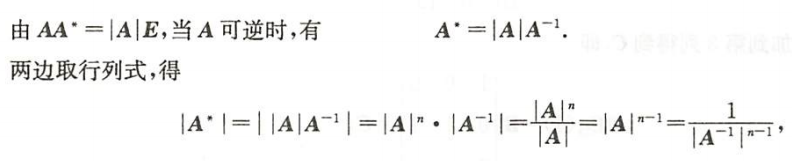
${\textstyle\unicode{x2465}}$ 三大运算的线性加:只有转置满足加法可拆性
${\textstyle\unicode{x2466}}$ 单位矩阵$\mathbf{E}$的三大运算结果还是单位矩阵$\mathbf{E}$
矩阵的逆
定义
矩阵逆的定义

设$\mathbf{A}$为$n$阶方阵,若存在$n$阶方阵$\mathbf{B}$,满足$\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}=\mathbf{E}$,则称矩阵$\mathbf{A}$可逆,$\mathbf{B}$是$\mathbf{A}$的逆矩阵,记为$\mathbf{A}^{-1}$,即$\mathbf{B}=\mathbf{A}^{-1}$
必须是方阵才能谈逆矩阵
可逆的充要条件是$\mathbf{A}$不为$\mathbf{0}$ $\iff \text{对应的}n$个向量线性无关
定义法证两个方阵可逆:凑两个方阵能等价相乘$\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}=\mathbf{E}$
凑的方法其实就是“凑完全平方”
性质与公式
凑$\mathbf{E}$的方法
用定义法求逆矩阵
三种方法
- 凑两个方阵能等价相乘$\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}=\mathbf{E}$
- 分解为$\mathbf{A}=\mathbf{B}\mathbf{C},\mathbf{B},\mathbf{C}\text{可逆},\mathbf{A}可逆$
- 法3分解成分块矩阵
$\color{red}{\text{求矩阵的逆}}$ 一共 $\color{green}{\text{三种方法}}$
- 用定义法求逆矩阵(一般是用来求抽象型问题)
- 用伴随矩阵求逆矩阵(用来解具体型)
- 用初等变换(初等矩阵)求逆矩阵(用来解具体型)
分块矩阵的逆
副对角分块,每个分块分别求逆,再倒着写
图片详情:副对角分块
主对角线元素的逆:每个主对角线元素的倒数
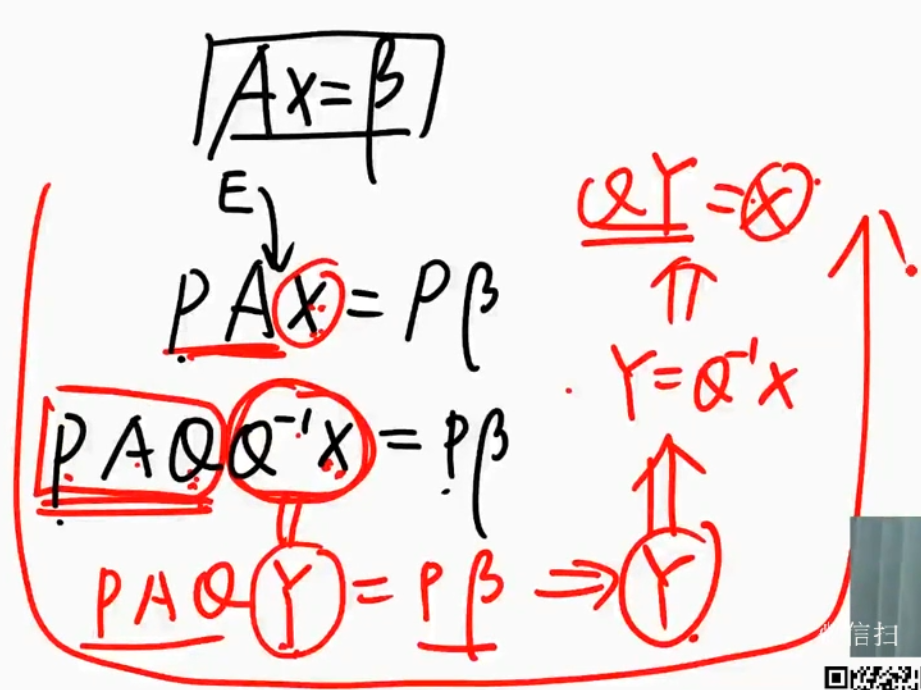
设方程
图片详情
$\color{red}{\text{证明矩阵A可逆}}$ , $\color{green}{\text{三种方法}}$
- A的行列式不为0
- 凑两个方阵能等价相乘$\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}=\mathbf{E}$
- 分解为$\mathbf{A}=\mathbf{B}\mathbf{C},\mathbf{B},\mathbf{C}\text{可逆},\mathbf{A}可逆$
$\color{red}{\text{Q}}$:这个矩阵怎么求逆矩阵: $\color{green}{\text{A}}$ 用初等变换的倍乘性质
图片详情
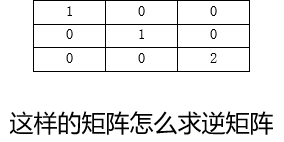
伴随矩阵
伴随矩阵是对方阵而言的
行的余子式,写到列里面去
$\mathbf{A}\mathbf{A}^\star=\mathbf{A}^\star\mathbf{A}=|\mathbf{A}|\mathbf{E}$
以二阶为例的证明
三个天然成立的可交换,最后一个互为逆矩阵才可交换
定义
伴随矩阵的定义

注意:伴随矩阵,每一个元素求了代数余子式之后还需要 $\color{green}{\text{转置}}$ !!!
性质与公式
$(k\mathbf{A})(k\mathbf{A})^\star=\lvert k \mathbf{A} \rvert \mathbf{E}$将$k\mathbf{A}$看成狗
$|\mathbf{A}^\star|=|\mathbf{A}|^{n-1}$
推导:
用伴随矩阵求逆矩阵
$\mathbf{A}^{-1}=\dfrac{1}{|\mathbf{A}|}\mathbf{A}^\star$
步骤
- 先算行列式,$|\mathbf{A}|\neq 0$才能用
- 写出$|\mathbf{A}|^\star$
- 代入公式
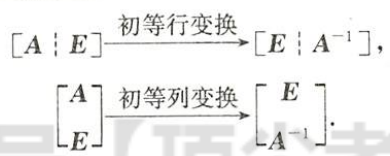
初等变换与初等矩阵
初等变换
(1)一个非零常$\color{green}{\text{数乘}}$矩阵的某一行(列);
(2)$\color{green}{\text{互换}}$矩阵中某两行(列)的位置;
(3)将矩阵的某一行(列)的k$\color{green}{\text{倍加}}$到另一行(列).
以上三种变换称为矩阵的初等行(列)变换,且分别称为$\color{green}{\text{倍乘}}$、$\color{green}{\text{互换}}$、$\color{green}{\text{倍加}}$初等行(列)变换.
$\color{green}{\text{左行右列法则}}$:矩阵左乘以初等矩阵就等于对矩阵进行一次初等行变换,矩阵右乘初等矩阵,就等于对该矩阵进行一次初等列变换,该定理简化了用矩阵乘法定义运算的过程。参考文献
初等矩阵
由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵,
(本书有自己的记号规范)
定义
性质与公式
(1)初等矩阵的转置仍是初等矩阵.
(3) 可逆$\mathbf{A}$一定可以经过有限次初等变换化成同阶单位矩阵$\mathbf{E}$
(4)对$n$阶矩阵$\mathbf{A}$进行初等行变换,相当于矩阵$\mathbf{A}$左乘相应的初等矩阵.同样,对$\mathbf{A}$进行初等列变换,相当于矩阵A右乘相应的初等矩阵.
用初等变换(初等矩阵)求逆矩阵
化成单位矩阵的方法
- 先往下加,再往上加
矩阵方程
$AX=B$
$XA=B$
$AXB=C$
矩阵的秩与等价矩阵
秩
定义
图片详情

初等变换不改变秩
图片详情

几个重要例子
有关秩的不等式
有关秩的不等式

遇到用不等式相关来解题的,化成对角阵,再来判断
等价矩阵
等价矩阵的定义

等价标准形揭示了经过有限次初等变换,秩为r的矩阵一定化为一个r阶单位阵被0围起来的样子
A、B同型等价矩阵 $\iff$ r(A)=r(B)
向量组
p341
线性代数的主人翁
熟悉矩阵相乘的形状
向量与向量组的线性相关性
如何判断向量组是线性相关的
- 按照定义如果能够线性凑一个等式,系数不全为0,那么线性相关
- 凑成两个矩阵的乘积取行列式,值不为0,则线性无关
向量定义
向量定义图片详情

线性组合
n个向量的线性组合
$\bigstar$ 线性表出
- 与非齐次方程组的解$\mathbf{A}x=\beta$联系
线性表出的定义
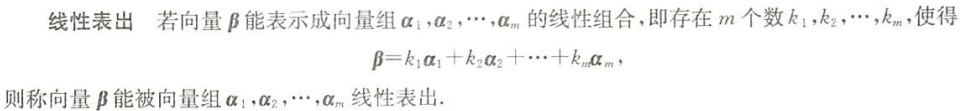
能表出
不能表出
$\bigstar$ 线性相关性
- 与齐次方程组的解$\mathbf{A}x=0$联系
用线性相关性的定义解题
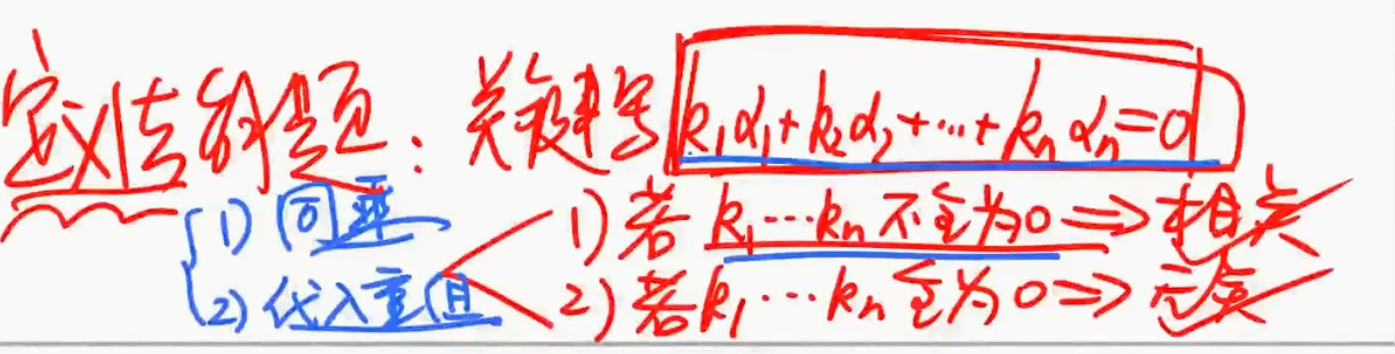
线性相关的定义

相关
含有零向量或有成比例的向量的向量组必线性相关.
如果只有一个向量且线性相关,这个向量是0向量
无关
n个向量线性相加得0,所有向量前面的系数都是0
判别的七大定理
定理1 向量组线性相关,其中一个向量可以由剩余的向量线性表示
图片详情

定理2 $\mathbf{\alpha}$之间线性无关,来了个$\mathbf{\beta}$线性相关,$\mathbf{\beta}$可以由$\mathbf{\alpha}$们线性表示
- 证明基本上都是定义法
图片详情

定理3 以少表多,多的线性相关
以少表多,多的线性相关

定理4:向量组线性相关的充分必要条件是齐次线性方程组$\mathbf{A}x=\mathbf{0}$有非零解
- 向量组中向量的维数小于个数(列数大于行数,形状横条),必然线性相关
- 向量组中向量的维数等于个数(行数等于列数,形状方形):行列式为0,线性相关;行列式不为0,线性无关
- 向量组中向量的维数大于个数(列数小于行数,竖条),1.先要化阶梯 2.
图片详情

图片详情

定理5 加一个线性相关的向量,秩不变
图片详情

定理6 部分相关,整体必相关
- 逆否命题成立。整体无关 $\implies$ 部分必无关
图片详情

定理7 原来无关 $\implies$ 延长无关
- 原来相关 $\implies$ 缩短相关(缩短其实应该是不一定的,万一把线性相关的都缩走了就不好了)
图片详情

极大线性无关组与向量组的秩
$\bigstar$ 极大无关组
- 极大线性无关:最简方程组
- 一个线性无关向量组的极大线性无关组就是向量本身
- 秩能表示极大线性无关组的个数
定义
图片详情

求法
求极大线性无关组的步骤
- 将向量组拼成矩阵$\mathbf{A}$,作初等行变换(在做同解变换),化为行阶梯矩阵,确定$r(\mathbf{A})$(向量组的秩)
- 按列找出一个秩为$r(\mathbf{A})$的子矩阵,即取为一个极大线性无关组
向量组的秩
- 向量组的秩,与矩阵的秩的关系:矩阵的秩就是它的行向量组(成或列向量组)的秩。(参考文献)
定义
图片详情
有关向量组的秩的重要定理和公式
被表出的秩不大
图片详情

$\bigstar$ 等价向量组
定义
两个向量组可以互相线性表出
向量组和他的极大线性无关组是等价的
判别
与等价矩阵的区别
等价矩阵和等价向量组的概念与区别
- 矩阵:$\mathbf{A},\mathbf{B}\text{同型}$:$\mathbf{A}\text{与}\mathbf{B}$等价$\iff r(\mathbf{A})=r(\mathbf{B})$ ($\mathbf{P}\mathbf{A}\mathbf{Q}=\mathbf{B}$)
- 等价向量组:$\mathrm{I}$,$\mathrm{II}$(同维即可) $\iff r(\mathrm{I})=r(\mathrm{II})=r(\mathrm{I|II})$
- 单方表出则互相表出
- $\blacktriangleright$(按照例2.3.14的说法,难道两个秩相等就能推出$r(\mathrm{I|II})$)
向量空间
概念
图片详情

基
坐标
维数
基变换与坐标变换
图片详情

变换公式
过渡矩阵
例题

线性方程组
p360
最主要的任务是求解
2021考了12分
增广矩阵
具体型线性方程组
齐次
- 齐次方程组必有零解
有解条件
当$r(\mathbf{A})=n$时,齐次方程组有唯一零解
当$r(\mathbf{A})=r<n$时,齐次方程组有非零解(有无穷多个解),且有$n-r$个线性无关解
- r是独立方程个数
解的性质
图片详情
$\bigstar$ 基础解系和解的结构
- 是方程组$\mathbf{A}\mathbf{x}=\mathbf{0}$的解
- 线性无关
- 方程组任意一解可以由基础解系线性表出
求解方法与步骤
- 作初等行变换化为阶梯型矩阵
- 按列找出一个秩为$r$的子矩阵,则剩余列位置的未知数即设为自由变量
- 按基础解系的定义写出通解
$\sharp$ 拓展:为什么只能做初等行变换,做初等列变换的时候会发生什么
求解方法与步骤(学校课件)

非齐次
- $\mathbf{b}$能不能线性表出的问题
有解条件
$$
r(\mathbf{A})=r(\mathbf{A}|\mathbf{b}) \begin{cases}
=n \quad \text{唯一解} , & \cr
<n \quad \text{无穷多解} , &
\end{cases} \
r(\mathbf{A}) + 1=r(\mathbf{A}|\mathbf{b}) \quad \text{无解}
$$
图片详情

解的性质
图片详情

求解方法与步骤
非齐次的通解=齐次的通解+非齐次的一个特解
图片详情

抽象型线性方程组
有解条件与解的判定
两道例题

解的结构
理论依据

例题

基础解系的讨论
- 三个条件
例题

例题2

系数矩阵列向量与解的关系
- 方程组的解就是描述向量组中各向量之间数量关系的系数
理论依据

图片详情

两个方程组的公共解
- 联立两个方程组求解即可
- 求出关系,代回通解
- 令两个基础解系相等
理论依据

题目

法一
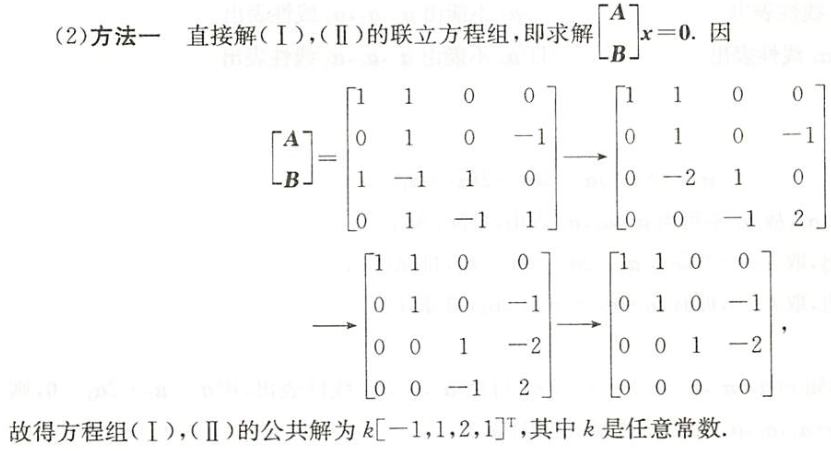
法二

法三

同解方程组
- 通解要求解全相等
- 公共解只是两个解的交集
理论依据

两道例题

特征值与特征向量
p379
此讲的矩阵均为方阵
总结一下每一讲对形状的限制
1.行列式,一定是方阵 $\mathbf{A}_{n\times n}$
2.矩阵,没有限定形状,$\mathbf{A}_{m \times n}$
3.向量组,没有限定形状,$\mathbf{A}_{m \times n}$
4.方程组,没有限定形状,$\mathbf{A}_{m \times n}$
5.特征值,一定是方阵 $\mathbf{A}_{n\times n}$
6.二次型,一定是方阵 $\mathbf{A}_{n\times n}$
特征值与特征向量
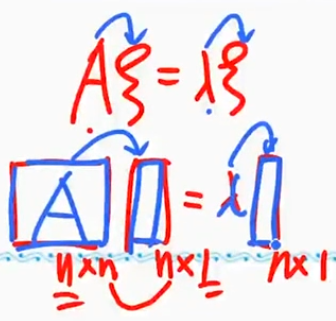
定义
定义

$\mathbf{A}\mathbf{\xi}=\lambda \mathbf{\xi}$
$\mathbf{\xi}$是$\mathbf{A}$的特征值,$\mathbf{\xi}$是$\mathbf{A}$的特征向量
$|\lambda \mathbf{E}- \mathbf{A}|=0$特征方程
性质
上下三角矩阵与对角矩阵的特征值就是对角线元素
特征值的性质
特征值加起来等于迹$tr(\mathbf{A})$
特征值乘起来等于行列式的值
特征向量的性质
(1) $k$重特征值$\lambda$至多只有$k$个线性无关的特征向量(直接使用无需证明)(例2.5.1)
(2) 若$\xi_1,\xi_2$是$\mathbf{A}$属于不同特征值的特征向量,则$\xi_1,\xi_2$线性无关(例2.5.5)
(3) 若$\xi_1,\xi_2$是$\mathbf{A}$属于同一特征值的特征向量,则$k_1\xi_1+k_2\xi_2$仍是$\mathbf{A}$属于特征值$\lambda$的特征向量(例2.5.7)
常用矩阵的特征值和特征向量
常用矩阵的特征值和特征向量

求法
具体型矩阵
注:不能有0解,不同时为0
提出法
试根法(试-1,1,0,最高次项的系数是1:试0次项的因子)
- $\bigstar$ $\bigstar$ $\bigstar$ 多项式的带余除法(顶级方法)
抽象型矩阵
证明主要是用定义- $\bigstar$(A不是必定不可以求逆吗,A的行列式必须是0?) 答:特征方程不是A
- 最后一个的证明,塞到矩阵中间的一定是$\mathbf{E}$
- $\mathbf{A}^T$特征值不变,特征向量不知道
相似
矩阵相似
定义
图片详情

性质
相似矩阵的性质

- 秩,行列式,特征方程 ,特征值相同,迹相同
- 对应的的矩阵多项式和矩阵的幂也相似
- 对应的逆矩阵也相似
- 对应的转置也相似
- A的伴随和B的伴随也相似
两个矩阵是否相似的判别与证明
两个矩阵是否相似的判别与证明

矩阵的相似对角化
- 回答为什么要求特征值和特征向量
能否相似对角化的例题1

能否相似对角化的例题2

定义
$\mathbf{P}^{-1}\mathbf{A}\mathbf{P}=\mathbf{\Lambda}$,$\mathbf{\Lambda}$为对角矩阵,则称$\mathbf{A}$可相似对角化,$\mathbf{\Lambda}$是$\mathbf{A}$的相似标准型
矩阵的相似对角化的定义
可相似对角化的条件
充分必要条件:$\mathbf{A}$有$n$个线性无关的特征向量
注:特征值与特征向量线性相关的关系
$$
\begin{cases}
\text{普通} \mathbf{A} \begin{cases}
\lambda_1 \neq \lambda_2 \implies \xi_1 \text{与} \xi_2 \text{无关} (\text{例2.5.5})\cr \cr
\lambda_1 = \lambda_2 \implies \begin{cases}
\xi_1 \text{与} \xi_2 \text{相关}(\text{例2.5.10(D)}) \cr \cr
\xi_1 \text{与} \xi_2 \text{无关} (\text{例2.5.10(C)})
\end{cases} \cr \cr
\end{cases} \cr \cr
\text{实际对称} \mathbf{A}\text{((必可相似对角化))}\begin{cases}
\lambda_1 \neq \lambda_2 \implies \xi_1 \perp \xi_2 (\text{例2.5.16})\cr \cr
\lambda_1 = \lambda_2 \implies \begin{cases}
\xi_1 \perp \xi_2 \cr \cr
\xi_1 \text{与} \xi_2 \text{无关}
\end{cases} \cr \cr
\end{cases}
\end{cases}
$$
两个充分
两个必要
实对称矩阵必可相似于对角阵

相似对角化的步骤
(1) 求$\mathbf{A}$的$\lambda$
(2) 求$\mathbf{A}$的$\lambda$的$\xi$
(3)令$P=(\xi_1\cdots \xi_2)$
应用
实对称矩阵的相似对角化
(1)$\mathbf{A}$是实对称矩阵,则$\mathbf{A}$的特征值是实数﹐特征向量是实向量(不用证)
(2)实对称矩阵$\mathbf{A}$的属于不同特征值的特征向量相互正交(证明见例2.5.16).
(3)实是对称矩阵的$\mathbf{P}$可以变换(正交化单位化)为正交矩阵
反问题
反求参数
反求参数的三种方法
反求$\mathbf{A}$
反求矩阵
$$
\begin{cases}
{\textstyle\unicode{x2460}} \mathbf{A}=\mathbf{P} \Lambda \mathbf{P}^{-1},(例2.5.21) & \cr
\bigstar {\textstyle\unicode{x2461}} \mathbf{A}^k=\mathbf{P} \Lambda^k \mathbf{P}^{-1} , & \cr
\bigstar {\textstyle\unicode{x2462}} f(\mathbf{A})=\mathbf{P} f(\Lambda) \mathbf{P}^{-1} , & \cr
\end{cases}
$$
两个矩阵是否相似的判别与证明
求$A^n\text{与}f(A)$
二次型
p407
二次型的定义与矩阵表示
二次型可以写为矩阵相乘的形式,$\mathbf{A}$为$f$的二次型矩阵,且$\mathbf{A}$是实对称矩阵
$f=X^T\mathbf{A}X$
写二次型矩阵的方法是$\mathbf{A}$的主对角线元素 $a_{ii}$ 是 $x_{i}^2$ 的系数, $a_{ij}$ 是 $x_i x_j$ 的系数一半
二次型矩阵是 $\color{green}{\text{对称矩阵}}$
图片详情

化二次型为标准形与规范形
二次型为标准形与规范形的定义
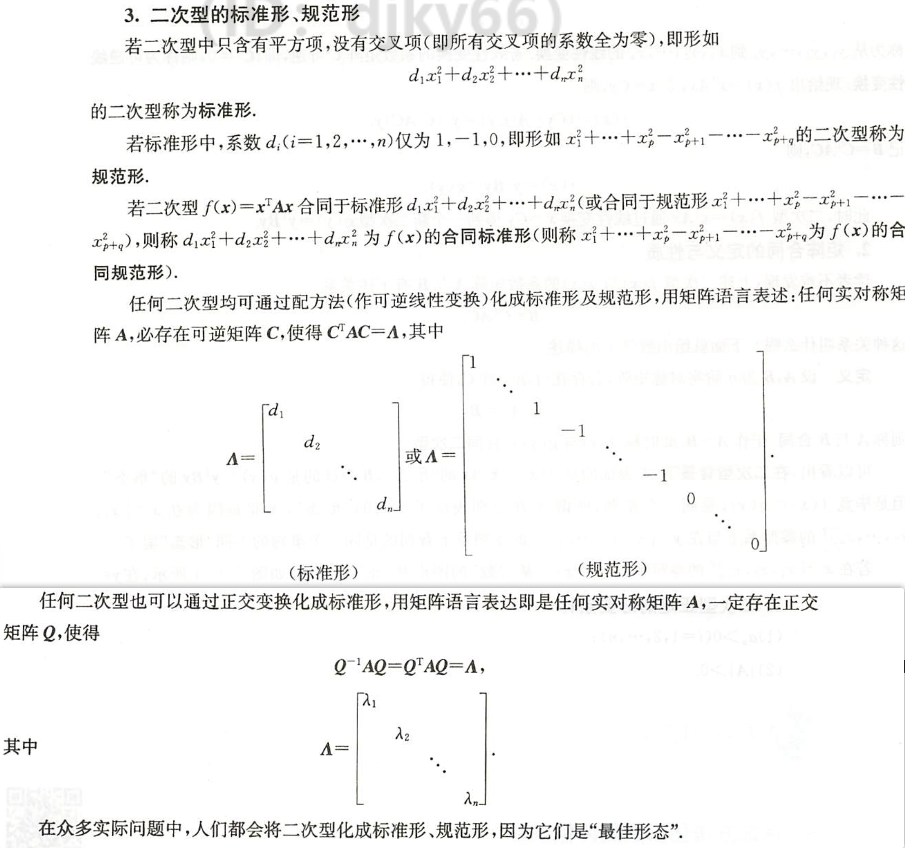
- 二次型的 $\color{green}{\text{标准形}}$ : 只含有完全平方项的二次型
二次型的标准形的定义
- 核心内容
- 联系p408
变换就是高等数学里面的换元
合同变换线性变换是可逆的变换就是合同变换
能够直接看出最大最小值的形状就是标准型,规范型
配方法
任何二次型均可通过配方法(作可逆线性变换)化成标准形及规范形,
二次型中含有完全平方项情形
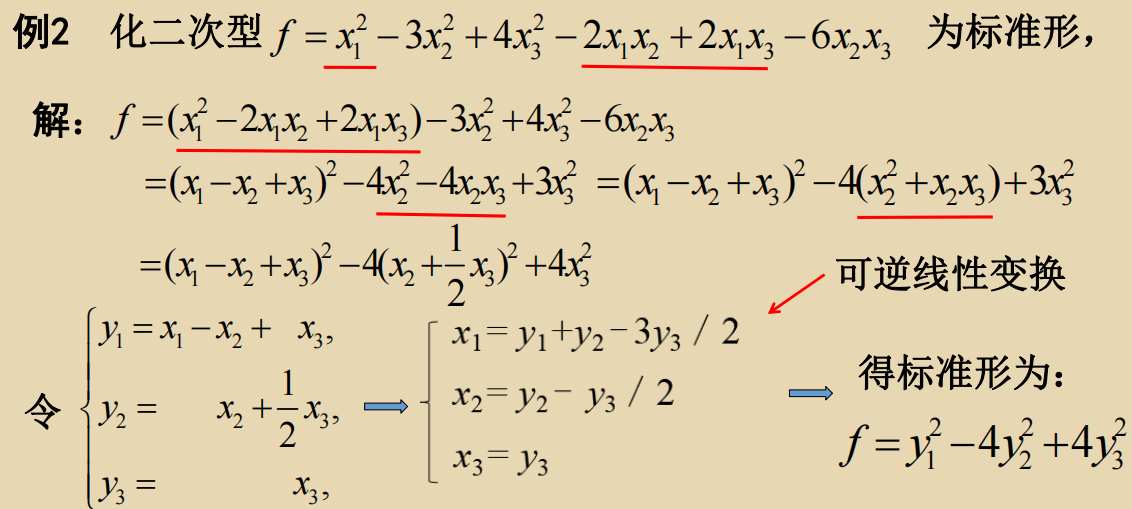
二次型中不含有完全平方项情形

正交变换法
任何二次型也可以通过正交变换化成标准形
图片详情

合同
图片详情

合同的充要条件是有相同的正,负惯性指数
合同的性质

惯性定理
标准型里面, $\color{green}{\text{正项}}$ 个数$p$与 $\color{green}{\text{负项}}$ $q$个数都是不变的,$p$称为正惯性指数,$q$称为负惯性指数
正定二次型
正惯性指数为n
二次型的前提是对称矩阵,讨论合同的前提是对称矩阵($\mathbf{A}^T=\mathbf{A}$)
定义
正定二次型的定义

充要条件
正定二次型的充要条件

必要条件
正定二次型的必要条件

判定
具体型二次型
选择题用主子式可能更快

抽象型二次型
- ${\textstyle\unicode{x2460}}$ 说对称
- ${\textstyle\unicode{x2461}}$ 说$\lambda$ 特征值全是0