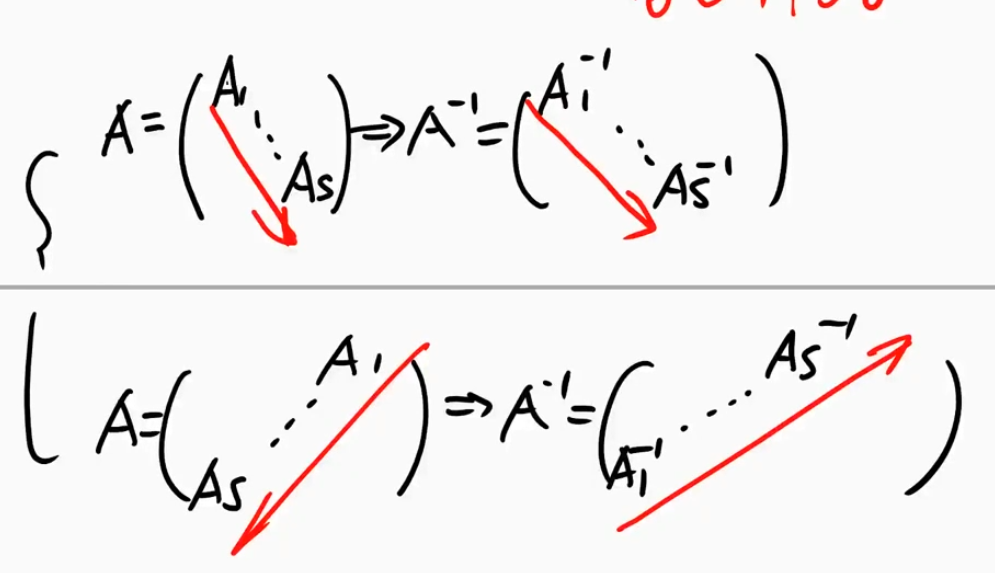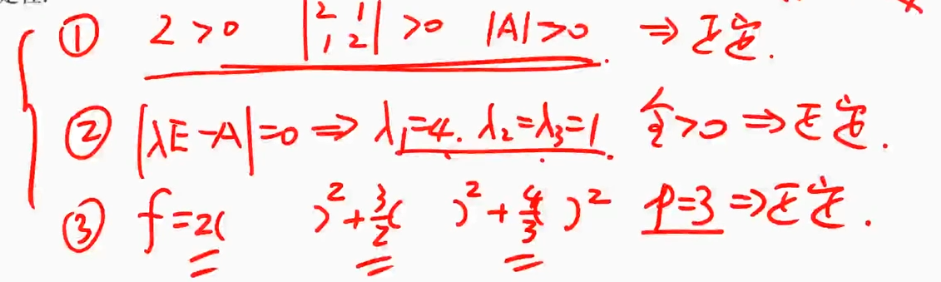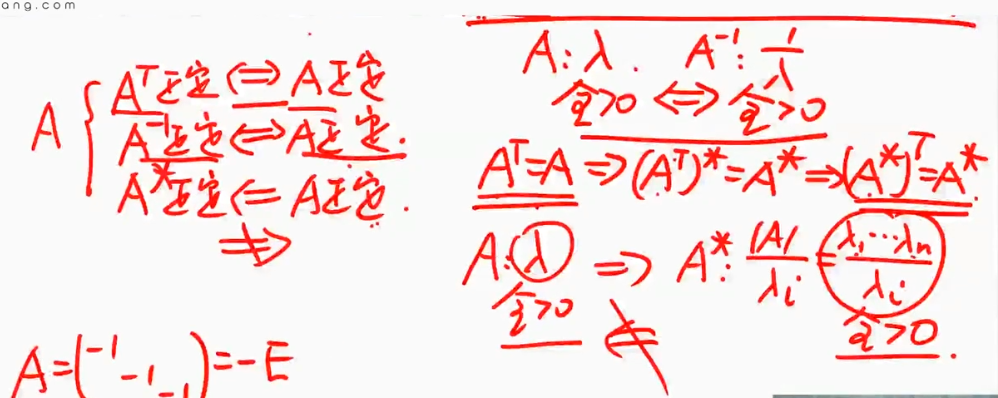凑数
凑数
凑数
凑数
ch1.行列式
例2.1.1
解析
- 直接展开法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.2
解析
- 爪型行列式
- 斜爪消平爪
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.3
解析
- 异爪型行列式
- 按照第四行展开,变成基本的三角行列式
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.4
解析
- 行(列)和相等
- 找相同的元素
例2.1.5
解析
- 拉普拉斯行列式
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.6
解析
- 范德蒙德行列式
- 把1整出来
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.7
解析
$\bigstar$ $\bigstar$ $\bigstar$
- 异爪型
- 递推法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.8
解析
- 行列式是一个函数
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.10
解析
$\bigstar$ $\bigstar$ $\bigstar$
- $\lambda$特征值
- 多项式的乘除法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.11
解析
- 用性质
- 抽象型行列式
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.12
解析
- 矩阵减
- 用公式$|AB|=|A||B|$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
习2.1.5
解析
- n阶一般用递推公式去做
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
习2.1.5
解析
- 异爪型
- 递推
- 按最下面一行展开,才能递推
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.1.13
解析
- 余子式与代数余子式的计算
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
习2.1.1
Details
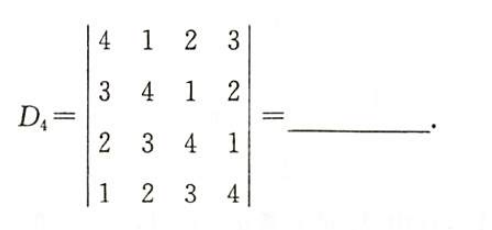
解析
160
Details

10被提出来了,后面又没有乘到答案里面
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 计算 | nan |
习2.1.4:范德蒙德展开
Details

解析
Details

- 想到了可能是范德蒙德展开,也想到了同时除以第一列,但是又完全没有想到
- 还需要用到$\lvert A^T \rvert= \lvert A \rvert$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 计算 | nan |
习2.1.5:递推式
Details

解析
Details

- 递推式按照第$n$行展开,会比较方便观察
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 计算 | nan |
例2.1.8:行列式与矩阵
Details

解析
Details

- 用初等行变化解的,数列交换的时候数错了
- 直接看成矩阵乘好了
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 计算 | nan |
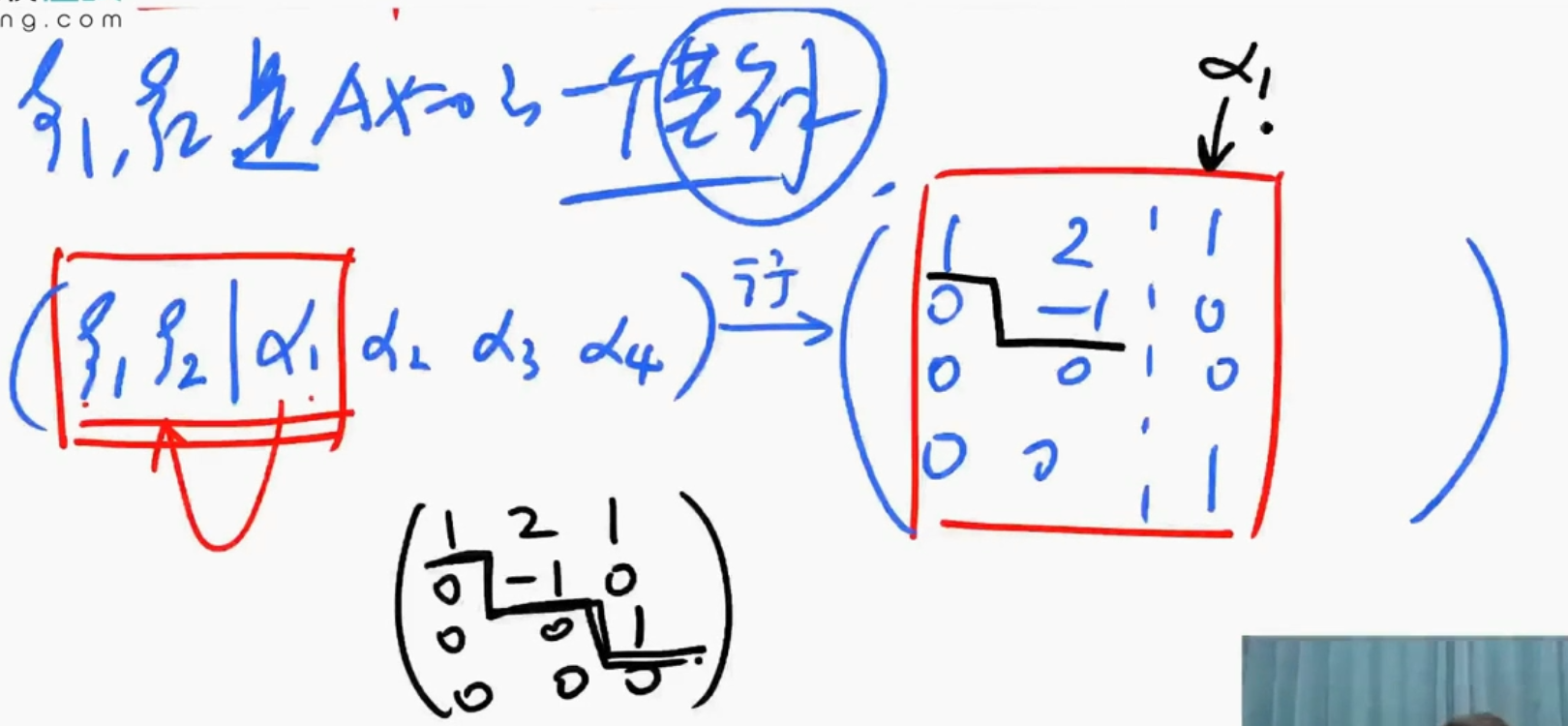
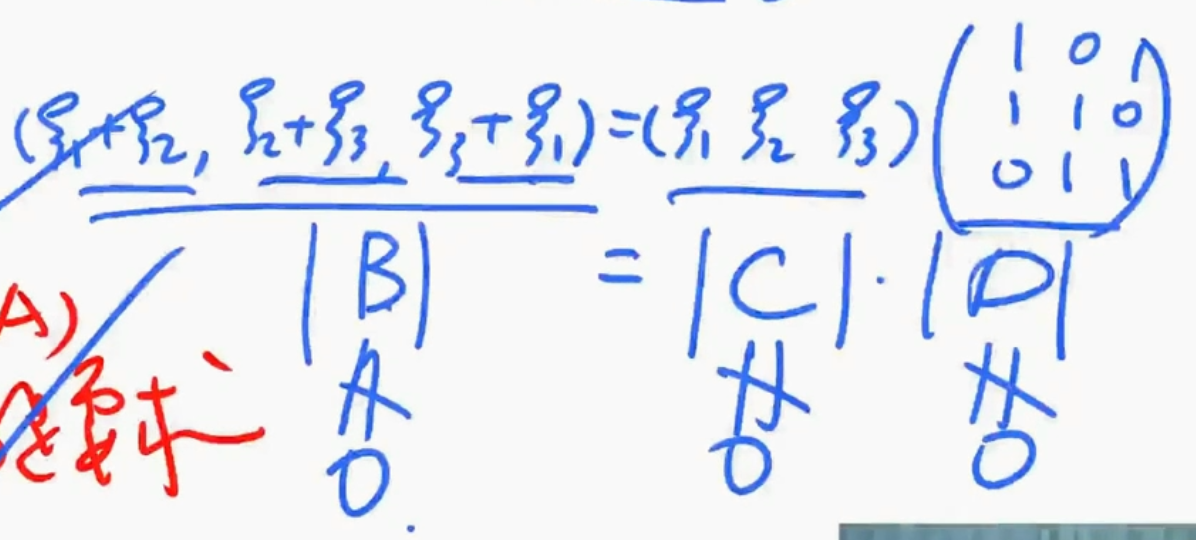
$\blacktriangle$ 初等行变换
图片详情

解析
图片详情
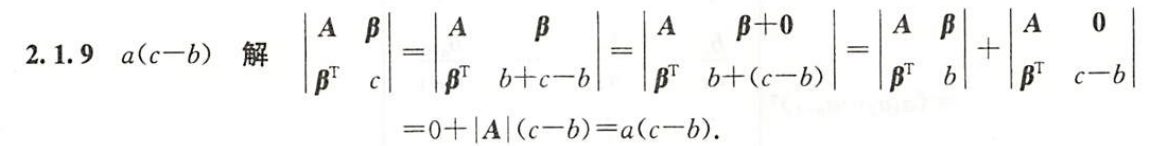
- 好题,加一列减一列
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 超越理解范围 | nan |
ch2.矩阵
例2.2.1
解析
- 行呈比例,可以反拆
- 运用结合律
- 拓展:$A^n=[tr(A)]^{n-1}A$
- 迹=$\sum a_{ii}$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.2
解析
- 稍微了解一下矩阵的运算法则
- 分奇偶
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.3
解析
- $\mathbf{A}^n$的运算,一共三种考题,强化拓展至5种
- $r(\mathbf{A})=1$ 例2.2.1
- 算$\mathbf{A}^2,\mathbf{A}^3$ 归纳出结果 例2.2.2
- $\mathbf{A}^n=(\mathbf{B}+\mathbf{C})^n=\cdots(\text{用展开式,前提可交换,其中有一个是}\mathbf{E})$
- 初等阵
- 相似对角化理论
- 跟幂函数的求导类似,只有前几项是有值的,后面都是0
稀疏矩阵中可能有门道
错因:算$\mathbf{A}^3$时用$\mathbf{A}^2 \times \mathbf{A}^2$来算了,实际上应该是$\mathbf{A}^2 \times \mathbf{A}^1$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 概念不清 | true |
例2.2.4
解析
- $\bigstar$
- 列方程
- 解:用$\color{red}{\text{矩阵初等变化}}$,或者高中的高斯消元,代入法
点乘为0就是正交,正交向量不需要转置
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 概念不清 | true |
例2.2.5
解析
- 施密特正交化方法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.6
解析
$\bigstar$
- 对称矩阵:$\mathbf{A}^T=\mathbf{A}$
- 证明正交矩阵,用定义法$\mathbf{A}^T\mathbf{A}=\mathbf{E}$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.7
解析
- 用伴随矩阵求逆矩阵
- 二阶的逆矩阵背下来,口诀:主对调,副变号
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.8
解析
- 简单的用一下伴随矩阵求逆矩阵
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.9
解析
- 用初等行变换
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.10
解析
- 凑定义法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.10
解析
- 运用 A的伴随的重要的秩的值,例2.3.12的结论
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.11
解析
- 分解为若干可逆矩阵的乘积
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.13
解析
- 证明可逆:行列式不为0
- 求逆:列方程
- 结论记忆的方法口诀:
- 主对角线三角:主对角线:求逆,副对角线:左乘同行,右乘同列,添负号
- 副对角线三角:副对角线:换位置求逆,副对角线:左乘同行,右乘同列,添负号
对角阵的逆,对角线元素求倒数
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.19
解析
- 简单的对式子做变换即可
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.20
解析
- $\blacktriangleright$(只要等于$\mathbf{E}$所有的矩阵都可逆?为什么?)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.23
图片详情

解析
- 对$n$阶矩阵$\mathbf{A}$进行初等行变换,相当于矩阵$\mathbf{A}$左乘相应的初等矩阵.同样,对$\mathbf{A}$进行初等列变换,相当于矩阵A右乘相应的初等矩阵.
- 学校教的方法解这题好像更好(这个课程后面好像有讲)?
图片详情

$\color{red}{\text{Q}}$:这个好像要用到向量方程组的知识了,后面再来看看?第二讲09视频讲过这道题,但是没有扩展下面的知识点
求满足条件的全部矩阵p

总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
习2.2.5
解析
- A的伴随的伴随
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
习2.2.1:求矩阵的幂
图片详情

解析
图片详情

写成两个矩阵的乘积
用定义法证明可逆
图片详情

解析
图片详情
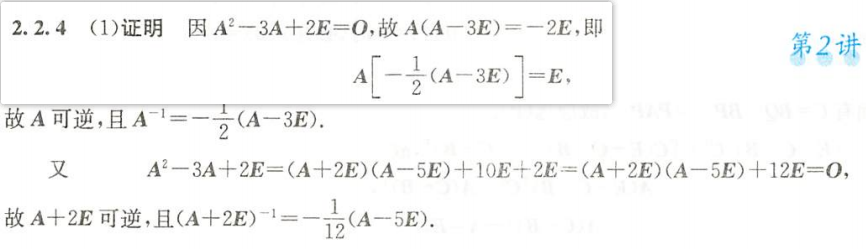
如果题目要求两个变量可逆,但是一步不能到位的话可以一个变量一个变量的求
ch3.向量组
例2.3.1
解析
- A:只说了s,没说其他不能互相线性表示
- B:$\beta = \mathbf{A}x$没有解才能证明不能线性表出
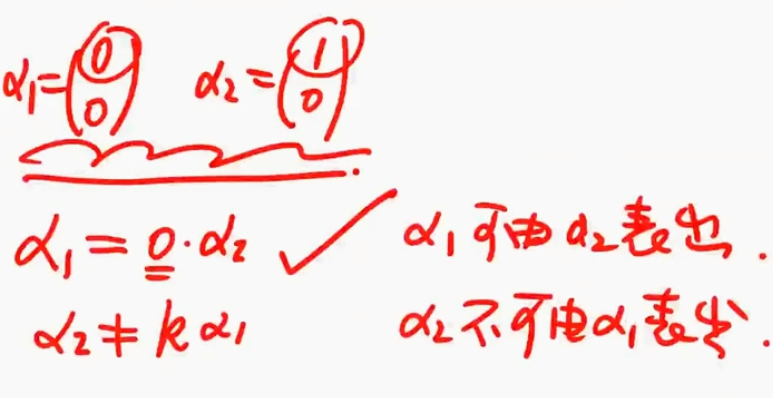
- C:线性相关至少有一个,并不是所有
- 线性表出和线性相关的概念不一样,我能被你表出,不代表你能被我表出(0可由非0表示。非0不能用0表示)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.3.5
解析
- 线性组合
- 代入重组
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.3.6
解析
- 用线性相关性定义法解题
- 同乘一个矩阵化简
- 学校课本上就有这道题
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.3.8
解析
- $\bigstar$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
2.3.9
解析
- $\bigstar$
- 求极大线性无关组的步骤:见笔记
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.3.10
解析
- 用定理:被表出的秩不大
- $\bigstar$ $\bigstar$ $\bigstar$ 这个结论经常用,重要的关于秩的不等式
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.10
解析
- 运用 A的伴随的重要的秩的值,例2.3.12的结论
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.2.11
解析
- 运用重要的有关秩的不等式 例2.3.10的结论
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.3.12
解析
- $\bigstar$ $\bigstar$ $\bigstar$ A的伴随的重要的秩的值
- p7 :00:16:00.000 ,不是很能听懂
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.3.14
解析
- 矩阵等价:两秩相同
- 求秩,可行可列,也可以混合(可行可列)变换
- 求极大无关组,只作行变换
- 求方程组,只作行变换
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.3.15
解析
- 运用公式轻轻松松
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
ch4.线性方程组
例2.4.1
解析
- 按照线性方程组的步骤求解齐次线性方程组
- 不要按照书本的答案来写,按照这个来写(这也是之前上课学的)
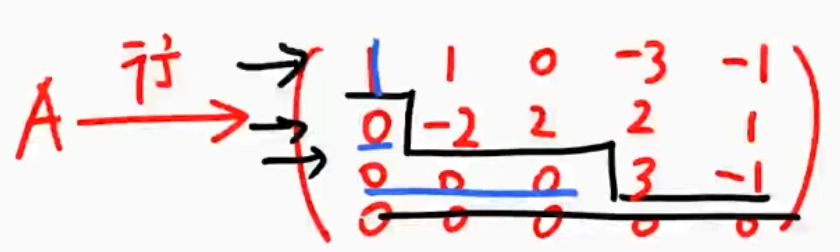
行阶梯型(消元)
- 若有0行,全在下方
- 从行上看,自左起出现连续0的个数自上而下严格单增
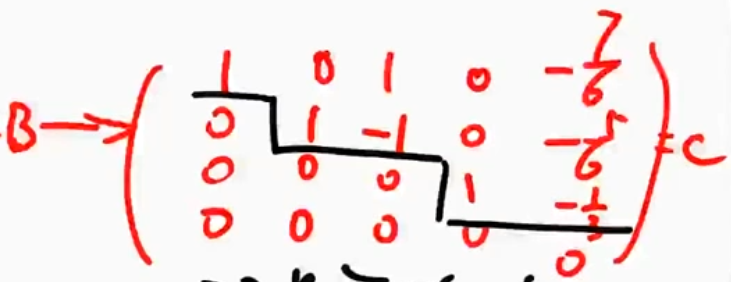
行最简阶梯型(代入)
- 若有0行,全在下方
- 从行上看,自左起出现连续0的个数自上而下严格单增
- 台脚元素为1
- 台脚正上方元素全为0
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.2
解析
- 先检查是否有解
- 求非齐次线性方程组
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.3
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.5
解析
- 抽象型有解问题
- $\mho$(没怎么听懂)
- A:$\mathbf{A}$线性无关和无关($r(\mathbf{A}) \leq n$)(列满秩)($\mathbf{A}x=0$有零解或无穷多解),和$\mathbf{\beta}$能不能被$\mathbf{A}$线性表示($r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta})$)($\mathbf{A}x=\mathbf{\beta}$有没有解)没有关系
- $\mathbf{A}x=\mathbf{\beta}$有唯一解 $\implies r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta}) = n \implies \mathbf{A}x=0$ 只有零解
- $\mathbf{A}x=\mathbf{\beta}$有无穷多解 $\implies r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta}) < n \implies \mathbf{A}x=0$ 有非零解,即有无穷多解
- A行满秩 $\implies r(\mathbf{A})=r(\mathbf{A}|\mathbf{\beta})$
- $\bigstar$(行满秩和列满秩的区别是什么)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.7
解析
- 写成增广矩阵的方式求解
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.8
解析
- 基础解系的题目,(线性无关)算行列式。
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.9
解析
- 系数矩阵列向量与解的关系
- 缺的补0
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.11
解析
- 令其基础解系相等
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.4.12
解析
- 2的解必为1的解
- 只要1的解满足2即可
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
习2。4.7
解析
- $\bigstar$ 极为重要的经典题目
- 设$A_{m\times n}$, 则$r(\mathbf{A})=r(\mathbf{A}^T)=r(\mathbf{A}\mathbf{A}^T)=r(\mathbf{A}^T\mathbf{A})$
- 15个关于秩的关系式
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
ch5.特征值与特征向量
例2.5.1
解析
- 解题技巧:由于行列式为0,所以秩最多是$n-1$
- 注:不能有0解,不同时为0
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
注2真题
解析
例2.5.4
解析
- 原理
- 只能是范围,不能是确实是
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.5
解析
- 证明题,思路就是用定义法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.8
解析
- 迹刚好是对角线元素之和
- 3阶伴随刚好为任意矩阵的
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.10
解析
- 能够相似对角化的条件
- B:有三个不同的$\lambda$必然有三个不同的$\xi$可以相似对角化(使用条件 ${\textstyle\unicode{x2462}}$ )
- C:$\bigstar$ $\bigstar$ $\bigstar$ 秩为1的话有技巧,有n-1个0,然后主对角线的和是另外一个特征值(使用条件 ${\textstyle\unicode{x2461}}$ )($\blacktriangleright$(这个算法的依据是什么))
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.12
解析
- 相似矩阵的传递性
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.6.3
改写为如下
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.16
解析
- 证明结论:实对称矩阵$\mathbf{A}$的属于不同特征值的特征向量相互正交(证明见例2.5.16).
- 穿脱原则
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.18
解析
- 两个矩阵相似,迹相同,行列式相同
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.20
解析
- 逆矩阵的特征值就是原矩阵的特征值
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.21
解析
- 反求矩阵的第一种方法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
习2.5.11
解析
- 反求矩阵的第二种方法
- 先讨论能不能相似对角化
- 讨论的对象中有参数,但是特征方程可能不含有参数
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.5.22
解析
- 反求矩阵的第三种方法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
ch6.二次型
例2.6.1
解析
- 用配方法化标准型
- 将某个变量的平方项与其混合项一次培成一个完全平方
- 直至全部配成完全平方即可
- n元要n换,缺项要补项
- 为什么补的项一定是$y_3=x_3$,不能是$y_3=x_2$之类的
- 一定要求逆
例2.6.2
解析
- 没有平方创造平方
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.6.3
解析
- 将二次型的定义具体化,形象化
- 正交变换法化为标准型
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.6.4
解析
- 合同理论(配方法)得到的不一定是特征值
- 相似理论得到的是特征值
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例2.6.5
解析
- 判断二次型的正定
- 4,5是非基础方法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |