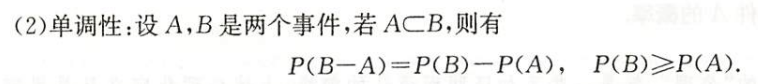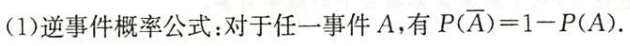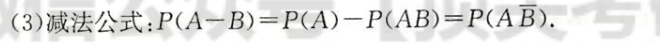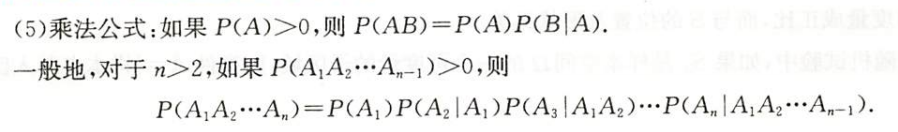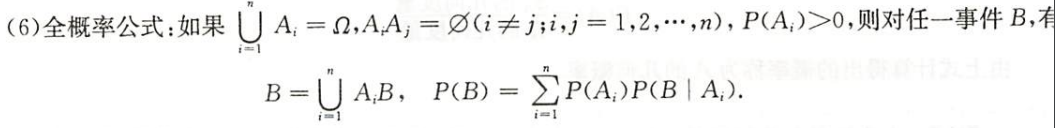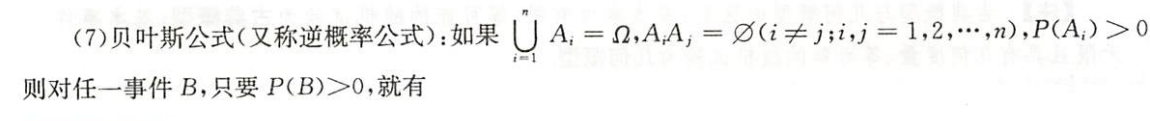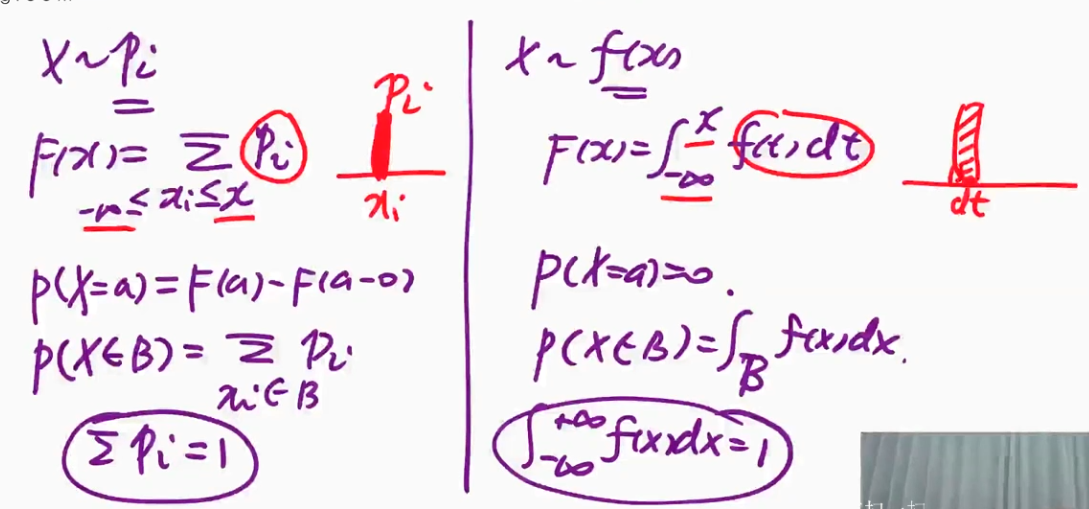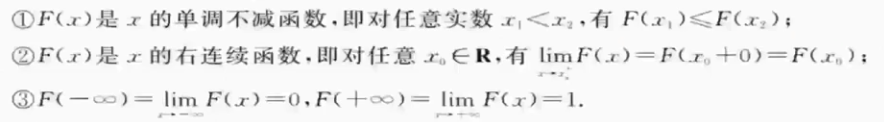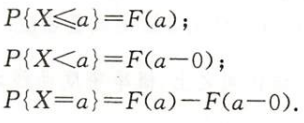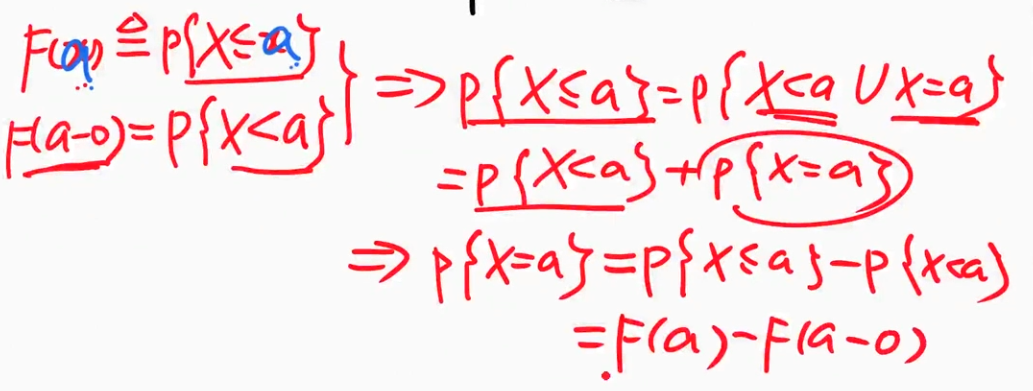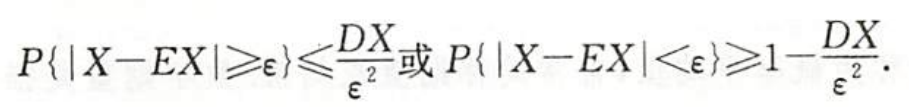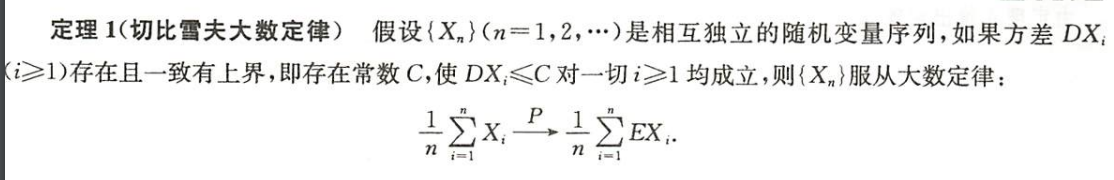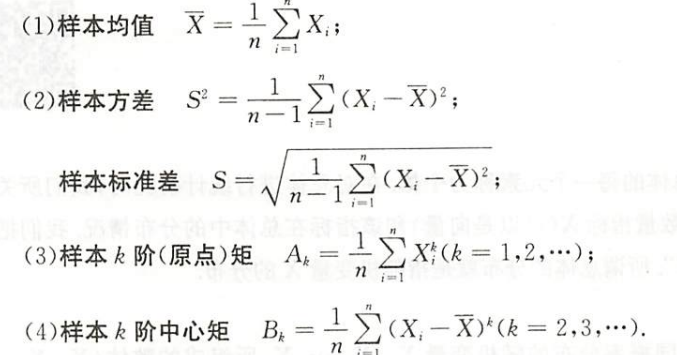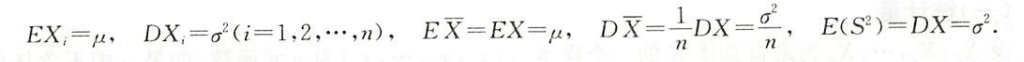zy2022-概率论与数理统计
随机事件与概率
p427
一般是5分小题
重要的三个考点
- 古典概型求概率
- 几何概型求概率
- 重要公式求概率
只考5个题?
基本概念
随机试验
$E$表示
(1)试验可以在相同的条件下重复进行;
(2)试验所有可能结果是明确可知道的,并且不止一个;
(3)每一次试验会出现哪一个结果,事先并不能确定.
随机事件
在一次试验中可能出现,也可能不出现的结果称为随机事件,简称事件,并用大写字母A,B,C等表示.为讨论需要,将每次试验中一定发生的事件称为必然事件,记为$\Omega$.每次试验中一定不发生的事件称不可能事件,记为$\emptyset$.
样本空间
随机试验的每一个可能结果(不可再分)称为样本点,记为$\omega$.样本点的全体组成的集合称为样本空间(或基本事件空间),记为$\Omega$,即$\Omega={\omega}$.由一个样本点构成的事件称为基本事件.随机事件A总是由若干个基本事件组成,即A是$\Omega$的子集.
事件的关系与运算
关系
包含
(1)如果事件A发生必导致事件B发生,则称事件B包含事件A(或A被B包含),记为A$\subset$B.
相等
(2)如果A$\subset$B且B$\subset$A,则称事件A与B相等,记为A=B.A与B相等,事实上也就是说,A与B由完全相同的一些试验结果构成,它不过是同一事件表面上看来两个不同的说法而已.
相容
(3)称“事件A与B同时发生”的事件为事件A与B的积(或交),记为A$\cap$B或AB.
(4)若AB$\neq \emptyset$,则称事件A和B相容;若AB=$\emptyset$,则称事件A与B互不相容,也叫互斥.如果一些事件中任意两个事件都互斥,则称这些事件是两两互斥的,或简称互斥的.
(5)称“事件A与B至少有一个发生”的事件为事件A与B的和(或并),记为A$\cup$B.
对立
(6)称“事件A发生而事件B不发生”的事件为事件A与B的差,记为A-B;称“事件A不发生”的事件为事件A的逆事件或对立事件,记为$\bar{A}$
由定义易知$A-B=A-AB=A\bar{B},\qquad B=\bar{A} \iff AB= \emptyset \text{且}A \cap B= \Omega$
(7)称有限个(或可列个)事件$A_1,A_2,\cdots,A_n,(\cdots)$构成一个完备事件组,如果$\displaystyle \bigcap_{i=1}^nA_i=\Omega,\quad A_iA_j = \emptyset(\text{对一切}i\neq j;i,j=1,2,\cdots,n(\cdots))$.
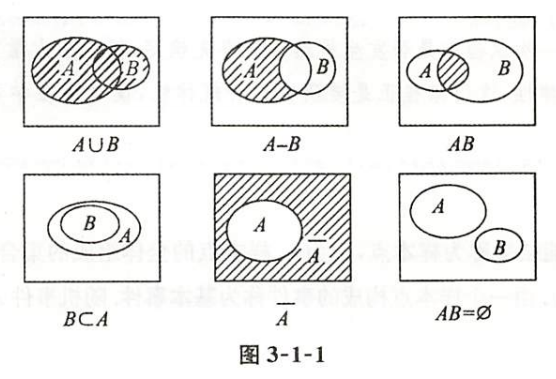
(8)事件的关系与运算可以用文氏图形象地表示出来(如图3-1-1),图中的矩形表示必然事件$\Omega$.
运算
和(并)
差
积(交)
运算法则
吸收律
交换律
结合律
分配律
$\bigstar$ 对偶律(德·摩根律)
概率的定义
描述性定义
通常将随机事件A发生的可能性大小的度量(非负值),称为事件A发生的概率,记为P(A).
统计性定义
在相同条件下做重复试验,事件A出现的次数k和总的试验次数n之比$\dfrac{k}{n}$,称为事件A在这n次试验中出现的频率.当试验次数n充分大时,频率将“稳定”于某常数的“附近”.n越大,频率偏离这个常数的可能性越小.这个常数p就称为事件A的概率.
公理化定义
每个事件的事件函数满足
(1)非负性
(2)规范性
(3)可列可加性
古典概型和几何概型
(1)称随机试验(随机现象)的概率模型为古典概型,如果其样本空间(基本事件空间)满足:
${\textstyle\unicode{x2460}}$ 只有有限个样本点(基本事件);
${\textstyle\unicode{x2461}}$ 每个样本点(基本事件)发生的可能性都一样.(等可能)
如果古典概型的基本事件总数为n,事件A包含k个基本事件,也叫作有利于A的基本事件为k 个,则A的概率为
$$
P(A) = \dfrac{k}{n}=\dfrac{\text{事件}A\text{所含基本事件的个数}}{基本事件总数}
$$
古典概型
不要研究的太过痴迷
数数法
(1) 枚举法
(2) 集合对应法
- 加法原理(n种方法,每种方法有m个)
- 乘法原理(n步骤,每个不走有m个方法)
- 排列
- 组合
- 逆数法(求对立事件数)
最主要的两个知识点:随机分配,简单随机抽样
随机分配
简单随机抽样
几何概型
${\textstyle\unicode{x2460}}$ 样本空间(基本事件空间)$\Omega$是一个可度量的有界区域;
${\textstyle\unicode{x2461}}$ 每个样本点(基本事件)发生的可能性都一样,即样本点落入$\Omega$的某一可度量的子区域S的可能性大小与S的几何度量成正比,而与S的位置及形状无关.
$$
P(A) = \dfrac{S_A\text{的几何度量}}{\Omega\text{的几何度量}}
$$
概率的基本性质与公式
性质
有界性
(1)有界性:对于任一事件A,有0≤P(A)≤1,且 P($\emptyset$)=0(不可能事件的概率是0),P($\Omega$)=1(必然事件的概率是1).
$P(A)=0 \nRightarrow A=\emptyset, \qquad A=\emptyset \implies P(A)=0$
- 例子,8.00-9.00内到达,8.30到达在几何概型里面概率是0,概率为0不一定不能发生
$P(A)=1 \nRightarrow A=\Omega, \qquad A=\Omega \implies P(A)=1$
- 例子,除了8.30不到,$\Omega$不是1
单调性
公式
逆事件概率公式
加法公式
减法公式
减法公式的推导
条件概率公式
乘法公式
全概率公式
全集分解公式
由因导果
贝叶斯公式(又称逆概率公式)
执果索因
信息增加后,有些事情的概率会变化
独立性
事件的独立性
(1)描述性定义(直观性定义)设A,B为两个事件,如果其中任何一个事件发生的概率不受另外一个事件发生与否的影响,则称事件A与B相互独立.
(2)数学定义设A,B为两个事件,如果P(AB)=P(A)P(B),则称事件A与B相互独立,简称为A与B独立.
事件的独立性的性质
$A\text{、}B\text{独立} \iff \bar{A} \text{、} \bar{B} \text{独立} \iff A \text{、} \bar{B} \text{独立} \iff \bar{A} \text{、} B \text{独立}$
n=3的情况
n重伯努利概型
n重伯努利概型

一维随机变量及其分布
p448
$\sharp$ 学科有研究对象和研究工具
- 数学上,研究对象(统一化,数字化)
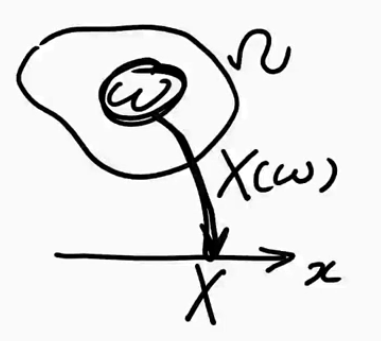
- (如上图)随机变量: 定义在样本空间上,取值在实数轴上的函数交随机变量$(r,v)\qquad X=X(\Omega)$
离散和连续随机变量的对比
八大分布是结构性知识
$f(x)\text{(密度)可以唯一确定}F(x)\text{(分布函数)}$,反之不然
- f(x)改变有限个值不改变,F(x)的值,在定积分里面学的
一维随机变量
概念
分布函数
分布函数的定义域一定是整个实数轴,x取遍$-\infty$导$+\infty$
研究范围从$\emptyset$(空集)一直到$\Omega$(全集)
概念
性质
- 单调不减
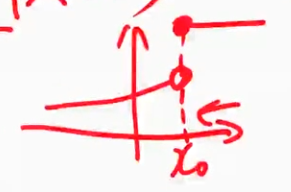
- 右连续(左空心右实心)(体现在题目上:等号跟着大于号,即例如$0 \leq x< 1$)
- 极限状态
- 有界性
应用——求概率
- 证明
a-0相当于左极限值
一维离散型随机变量
如果随机变量X只可能取有限个或可列个值,则称X为离散型随机变量
$X \backsim p_i$念作X服从$p_i$
需要掌握的知识点:
- 定义
- 所有概率加起来为1(归一性)
- 求一点函数的概率
- 求区间函数的概率
分布律
分布列,分布律,概率分布
性质
应用—求概率
五大分布
0-1分布$B(1,p)$
$$
\text{伯努利计数变量} X \backsim \begin{pmatrix}
1 & 0 \cr
p & 1-p
\end{pmatrix}
$$
即 $P\lbrace X=1 \rbrace=p,P\lbrace X=0 \rbrace =1-p$,称 $X$ 服从参数 $p$的0-1分布,记为 $X \backsim B(1,p)$
| 图片 | 要点 |
|---|---|
 | 独立实验 独立重复试验 伯努利试验 例子:投篮 |
二项分布$B(n,p)$
$P\lbrace X \rbrace = C_n^kp^k(1-p)^{n-k}$,称$B(n,p)$
泊松分布$P(\lambda)$
$$
P\lbrace X=k \rbrace = \dfrac{\lambda^k}{k!}e^{-\lambda}
$$
念作$X$服从参数为$\lambda$的泊松分布
$\lambda$是强度
作用:某场合某单位时间内源源不断的质点来流的个数。
- 例子:超市 8.00-9.00 源源不断的 客户来的个数
- 例子:节假日的人流
注意:也可用来研究稀有事件发生的概率
几何分布$G(p)$
首中即停
$$
p \lbrace X \rbrace =p(1-p)^{k-1}
$$
意义:
- 首次出现故障就停止,广泛应用在寿命分布中
- 守株待兔
超几何分布$H(n,N,M)$
古典概型的一种特殊情况
| 图片 | 要点 |
|---|---|
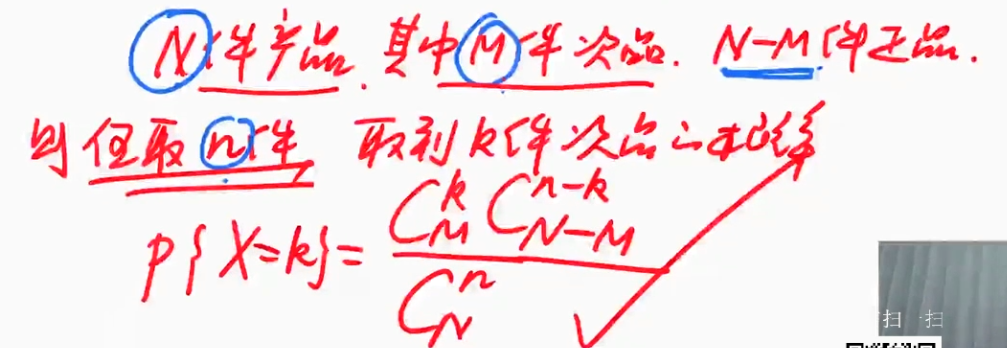 | 一个例子解释超几何分布 |
一维连续型随机变量
$X \backsim F(x)$ $\buildrel \rm \Delta \over{=}$ $p \lbrace X \leq x\rbrace=\int_{-\infty}^xf(t)dt$
- 被积函数是可积函数,其被积函数必然连续
需要掌握的知识点:
- 定义
- 所有概率加起来为1(归一性)
- 求一点函数的概率
- 求区间函数的概率
概率密度
性质
应用-求概率
三大分布
均匀分布
相当于几何概型的一维情形
| 图片 | 要点 |
|---|---|
 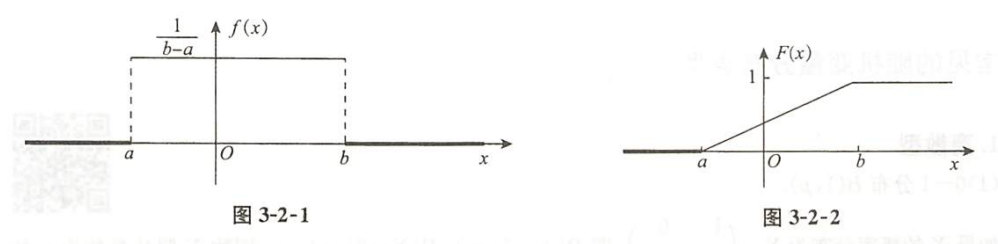 | 均匀分布的定义 |
高级说法:$X\text{在}I$上的任一子区间取值的概率与该子区间长度成正比$\implies$ $X \backsim U(I)$
指数分布
| 图片 | 要点 |
|---|---|
 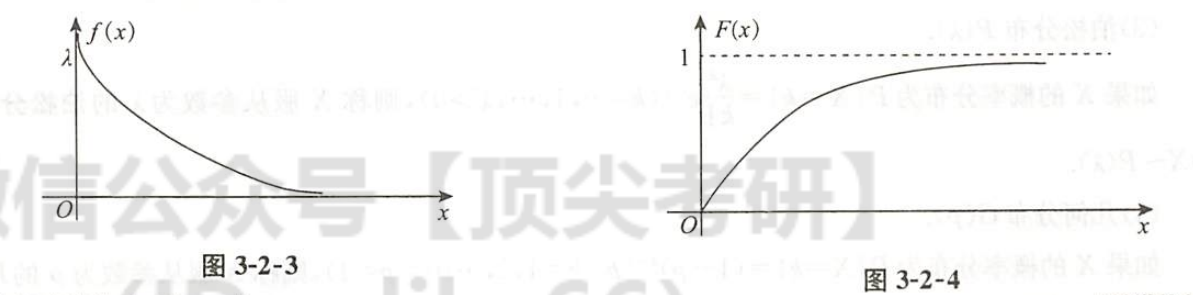 | 指数分布的定义 |
等待型分布(几何分布也是)
- 几何分布:离散
- 指数分布:联系
$\lambda$是机器坏的失效率,兔子来撞树
正态分布
| 图片 | 要点 |
|---|---|
 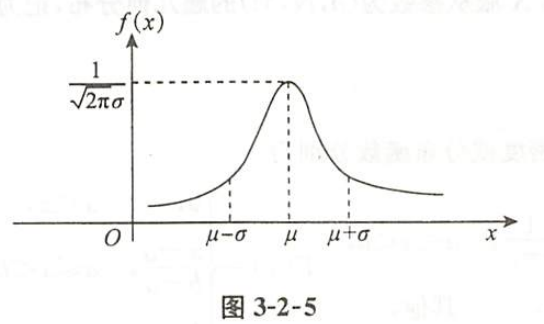 | 正态分布概率密度 |
| 图片 | 要点 |
|---|---|
 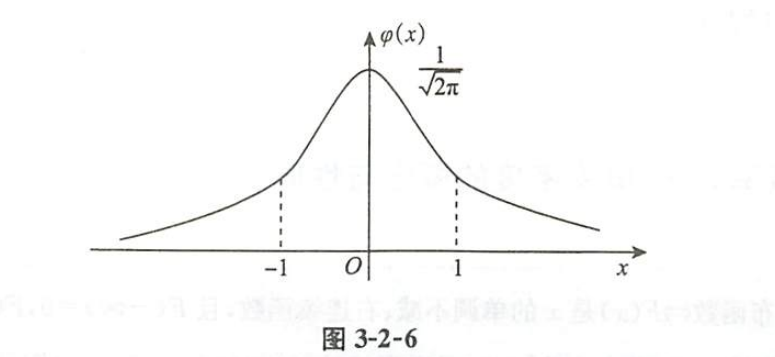 | 标准正态分布 |
| 图片 | 要点 |
|---|---|
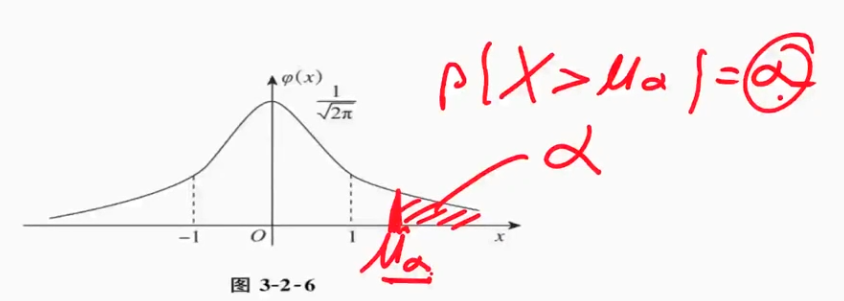 | 上$\alpha$分位点($\mu_\alpha$),右侧围出$\alpha$时,对应的点$\mu_\alpha$是多少 |
| 图片 | 要点 |
|---|---|
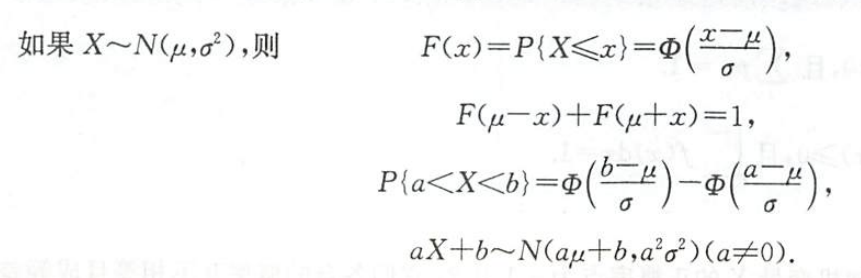 | 1.把正态分布标准化 2.用上$\alpha$的推导画图研究 3.正态分布的范围转化为标准正态分布的范围 正态分布的数字特征 |
一维随机变量函数的分布
| 图片 | 要点 |
|---|---|
 | 引论,射击游戏的积分制度 |
离散型→离散型
连续型→连续型(混合型)
解题步骤
多维随机变量及其分布
p472
三块知识点
- 定义
- 类型
- $\bigstar$ $\bigstar$ $\bigstar$函数的分布(大题考点)
四个新概念(相比于1维)
- 联合
- 边缘
- 条件
- 独立
$\text{条件}= \dfrac{\text{联合}}{\text{边缘}}$
独立性就是检验$\text{联合}=\text{边缘的乘积}$
二维(n维)随机变量
| 图片 | 要点 |
|---|---|
  | 总结, 独立性:对于每一个ij都是边缘概率的乘积 |
分布函数 $f(x,y)$ 与概率P{Y $\leq$ X}

概念
联合分布函数
| 图片 | 要点 |
|---|---|
 | 联合分布函数 |
概念
性质
边缘分布函数
| 图片 | 要点 |
|---|---|
 | 边缘分布函数 |
联合分布律
图片详情

边缘分布律
图片详情
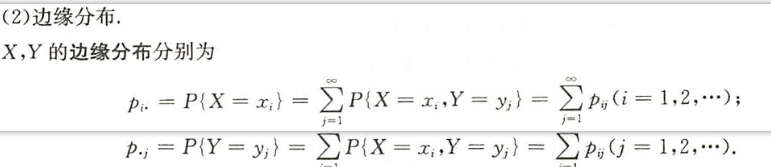
条件分布律
二维连续型随机变量
| 图片 | 要点 |
|---|---|
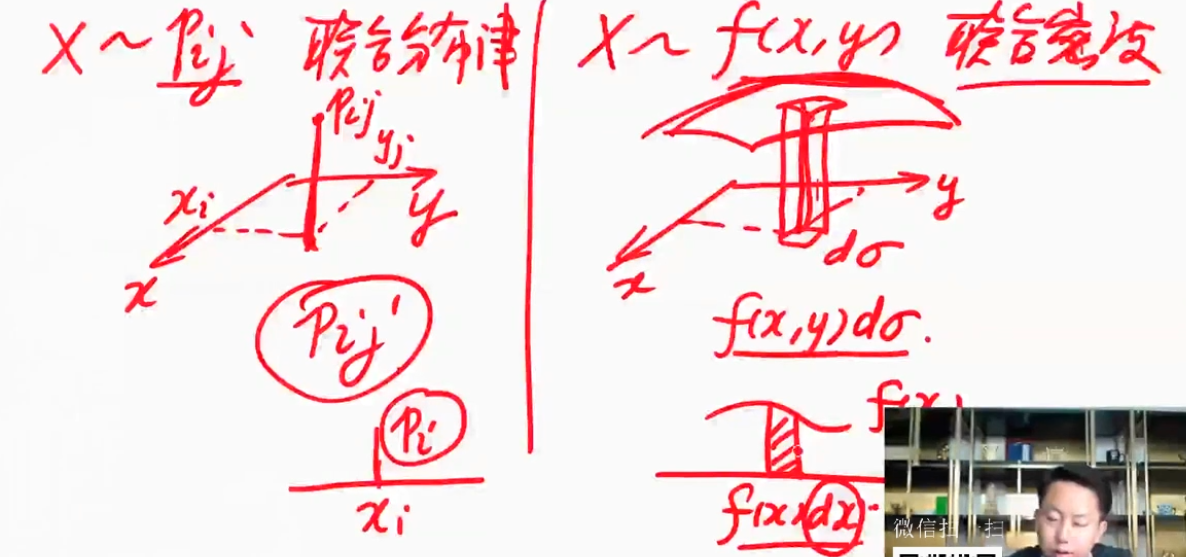 | 联系二维离散型随机变量和二维连续型随机变量 |
联合概率密度
图片详情

边缘概率密度
| 图片 | 要点 |
|---|---|
 | 求谁不积谁 不积先定限 限内画条线 先交写下限 后交写上限 |
条件概率密度
条件密度和条件分布函数

即 $\text{条件}=\dfrac{\text{联合}}{\text{边缘}}$
联合分布函数与概率密度、边缘概率密度、条件概率密度
联合分布函数与概率密度、边缘概率密度、条件概率密度

二维均匀分布
二位均匀分布就是几何概型
二维均匀分布与定义、例题
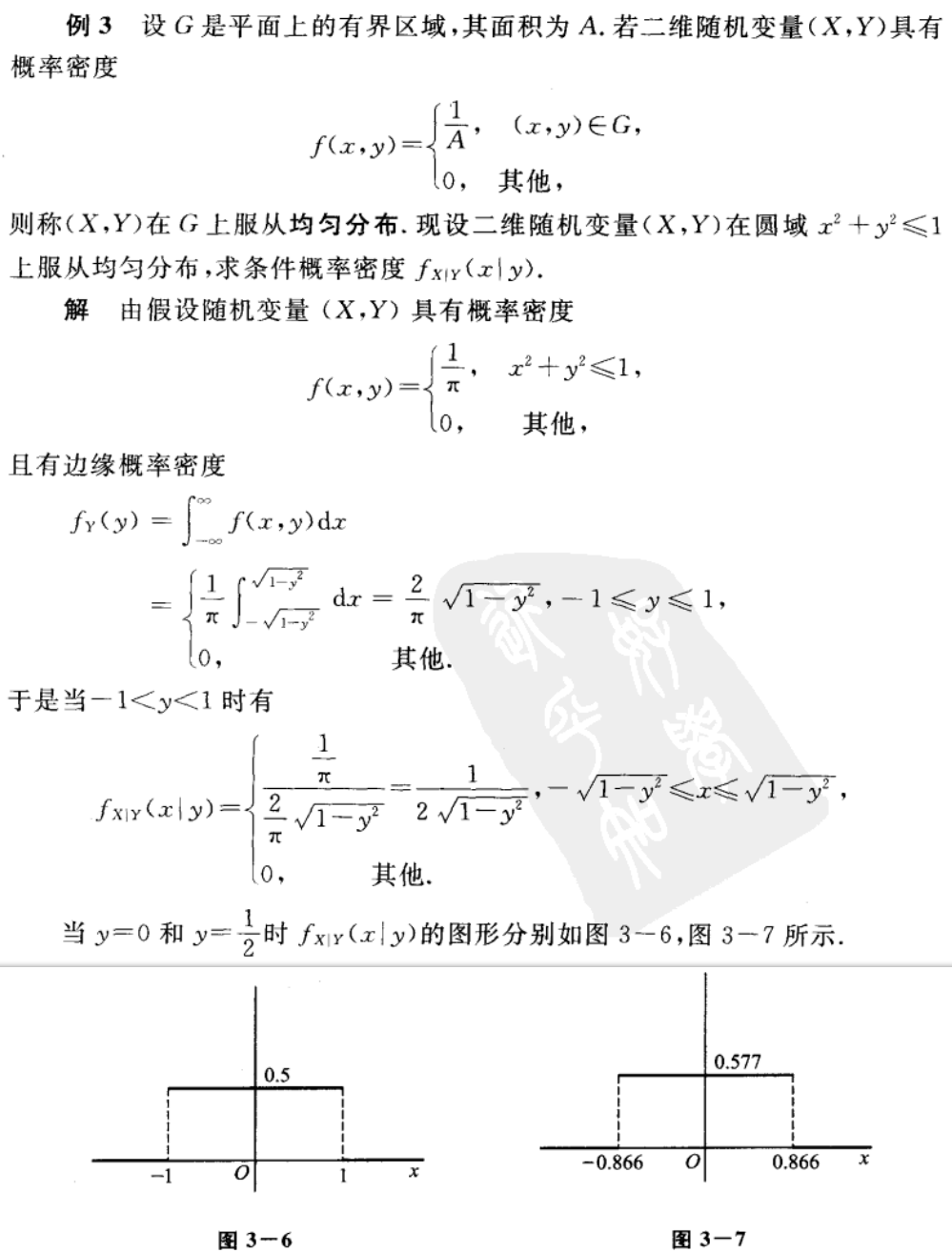
二维正态分布
图片详情

要考就考数字特征
独立性
- 两个以上变量就会关注独立性
| 图片 | 要点 |
|---|---|
 | 注意对比原来的公式,实际做题还要交$G_{\text{正}}$ |
概念
相互独立的充要条件
$F(x,y)=F_X(x)\cdot F_Y(y)$
$P_{ij}=P_i\cdot P_j$
$fx,y)=f_X(x)f_Y(y)$
性质
图片详情

独立的性质

函数的分布
| 图片 | 要点 |
|---|---|
 | U实际上是一维的 |
(离散型,离散型)→离散型
(连续型,连续型)→连续型
分布函数法
卷积公式
记忆方法:
- 积谁不换谁
- 换完求偏导
| 图片 | 要点 |
|---|---|
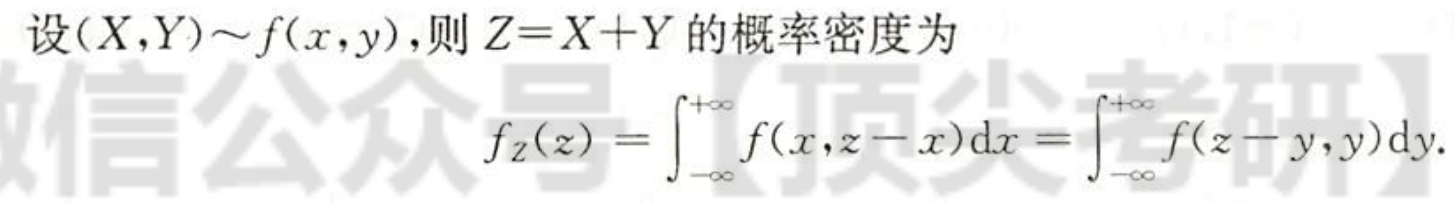   | 和的分布, 注:证明的蓝色部分是要求掌握的,涉及高等数学的知识 |
| 图片 | 要点 |
|---|---|
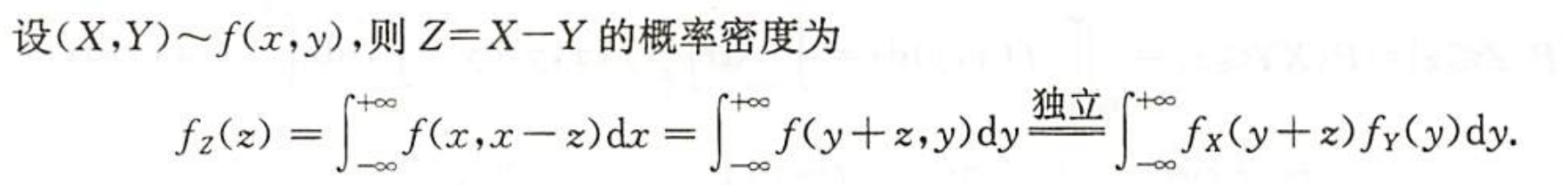 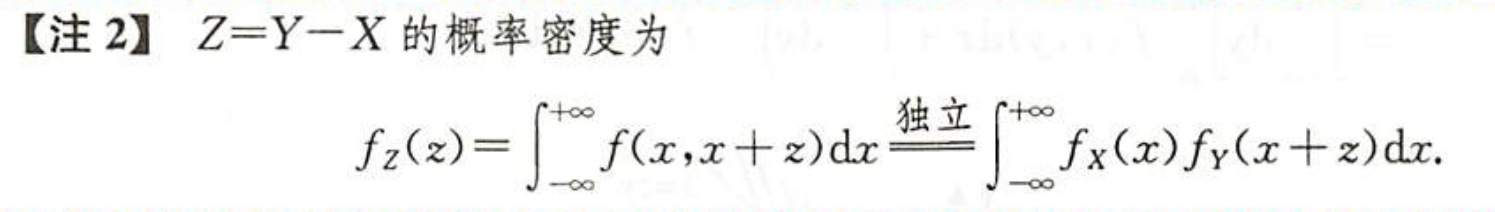 | 差的分布 |
| 图片 | 要点 |
|---|---|
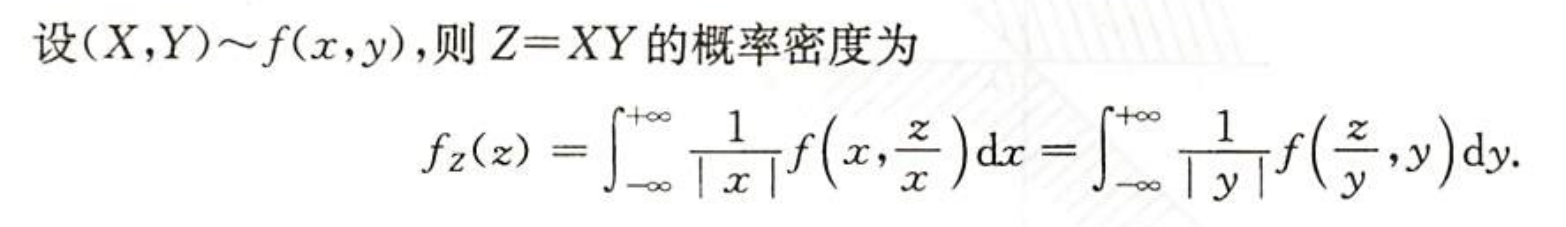 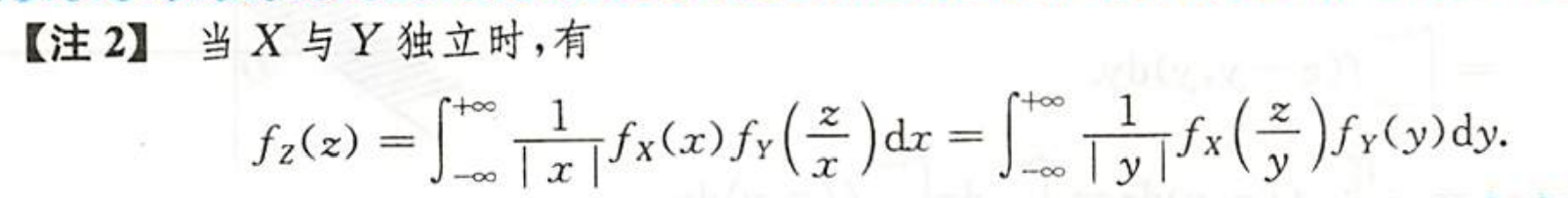 | 积的分布 |
| 图片 | 要点 |
|---|---|
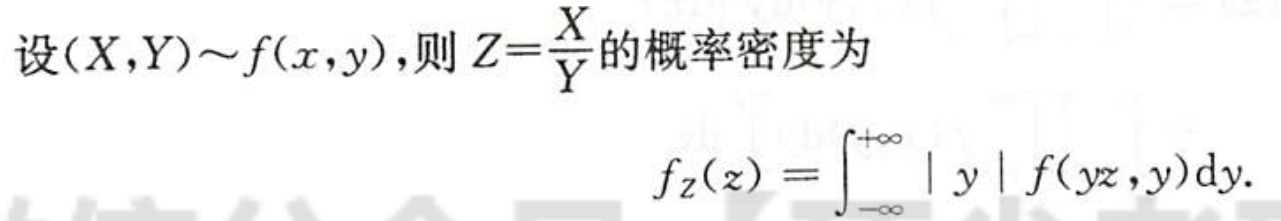 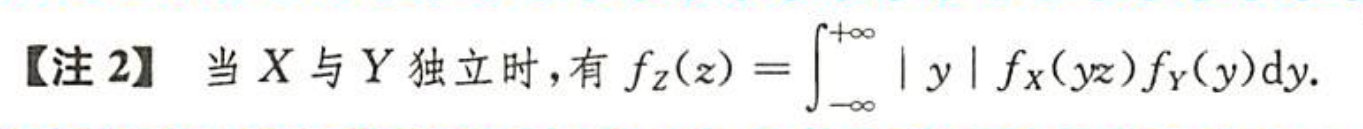 | 商的分布, 只记y的比较好求 |
max的分布
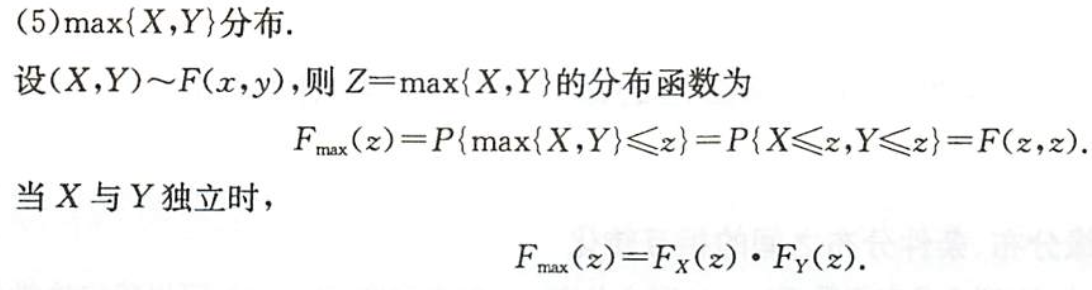
min的分布

n个相互独立的随机变量

分布的可加性

(离散型,连续型)→连续型
(离散型,连续型)→连续型使用全概率公式
图片详情

随机变量的数字特征
p500
引论:有的时候不需要知道概率分布,只需要知道数字指标
四个重要的知识,1个综合知识:
- E(x)数学期望
- D(x)方差
- Cov(x,y)协方差
- $\rho_{xy}$相关系数
- 不相关也能证明独立性
$\blacktriangleright$(为什么方差和期望啥的不需要小括号)
一维随机变量的数字特征
数学期望
是一个合理的平均值
概念
| 图片 | 要点 |
|---|---|
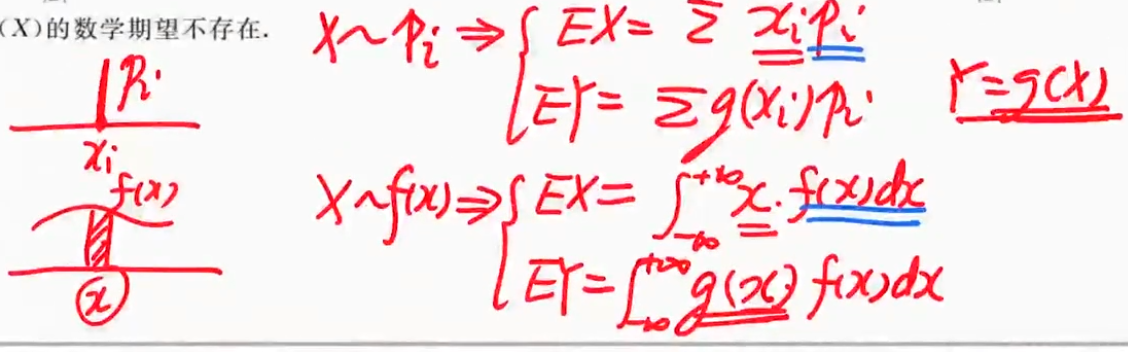 | 离散和连续的数学期望的定义 |
性质
| 图片 | 要点 |
|---|---|
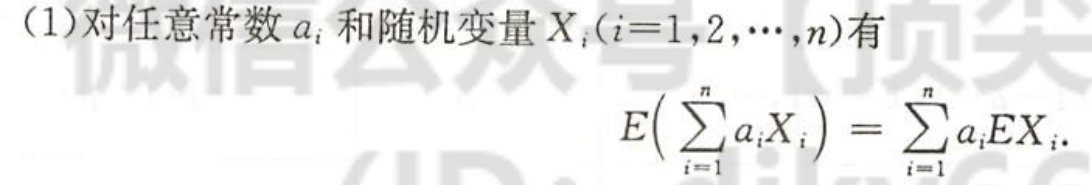 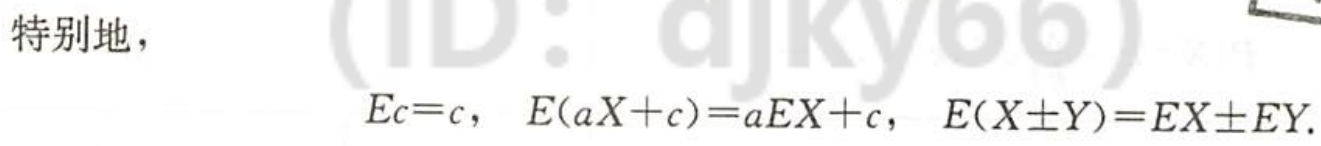 | 和差是无条件打开的 |
常数的期望是期望本身
独立的时候,乘积的方差才是方差的乘积
方差、标准差
引论:派运动员去参加运动会,选方差小的
概念
$DX=EX^2-(EX)^2$
性质
$EX^2 \geq (EX)^2$
| 图片 | 要点 |
|---|---|
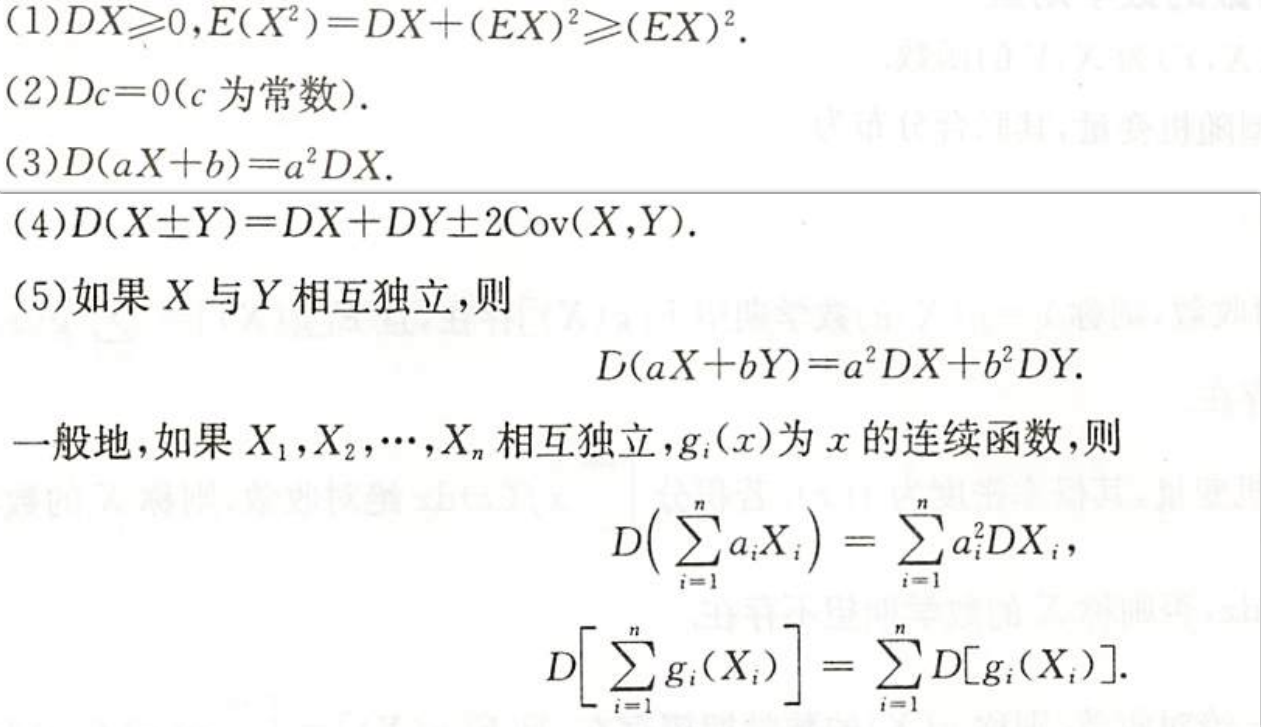 | 方差的性质 |
| 图片 | 要点 |
|---|---|
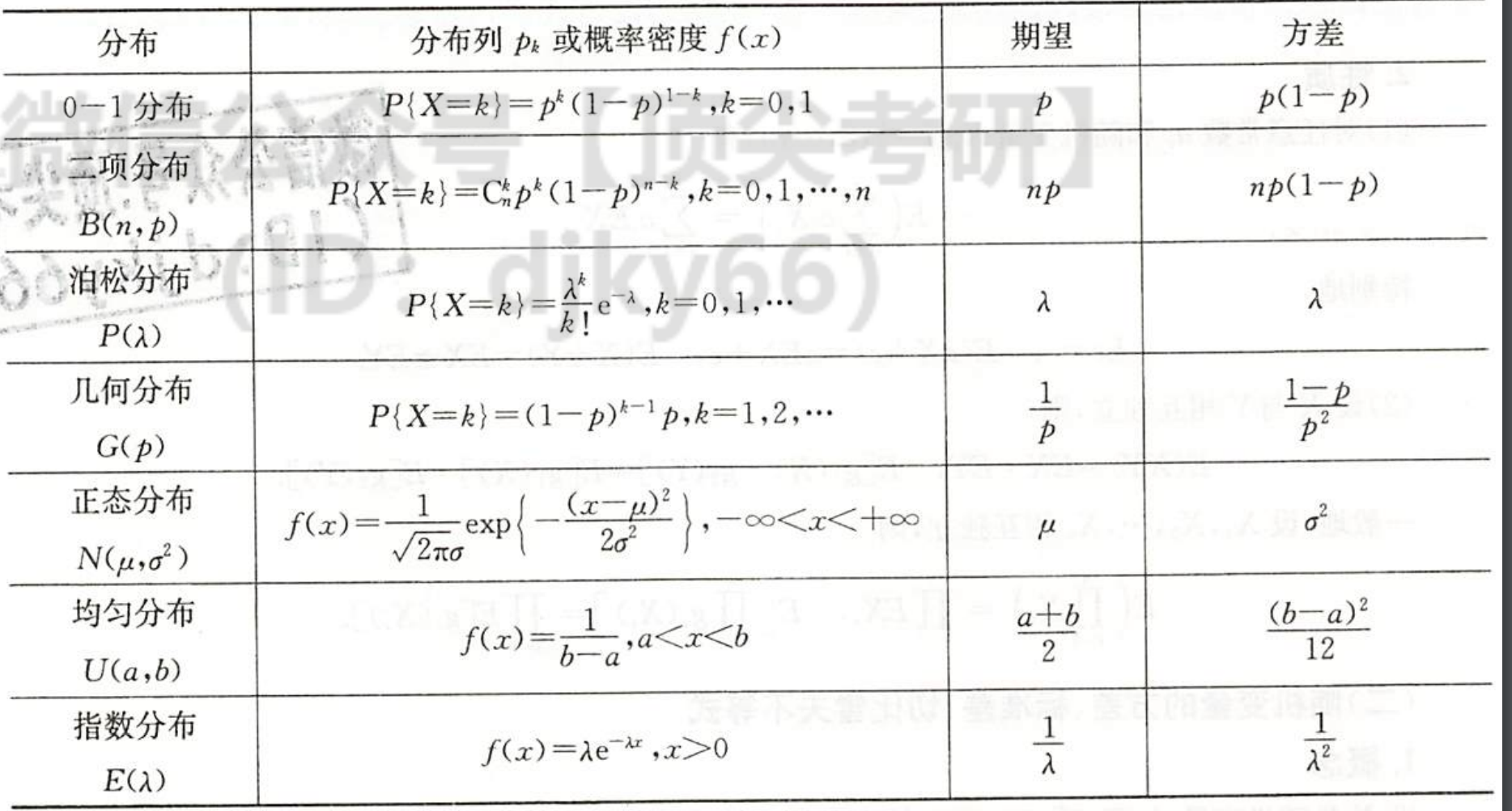 | 没有超几何分布 |
切比雪夫不等式
引论:描述了一次射击和这个运动员的平均水平的差距的关系,距离大于某个值的概率是不大的(第6讲也会用到)
二维随机变量的数字特征
数学期望
| 图片 | 要点 |
|---|---|
 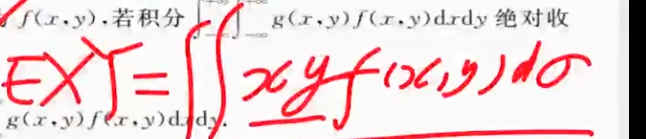 | 二维联合概率的数学期望计算 一般是协方差的一个步骤(红字部分) |
协方差与相关系数
概念
| 图片 | 要点 |
|---|---|
 | 协方差与相关系数的定义 |
| 图片 | 要点 |
|---|---|
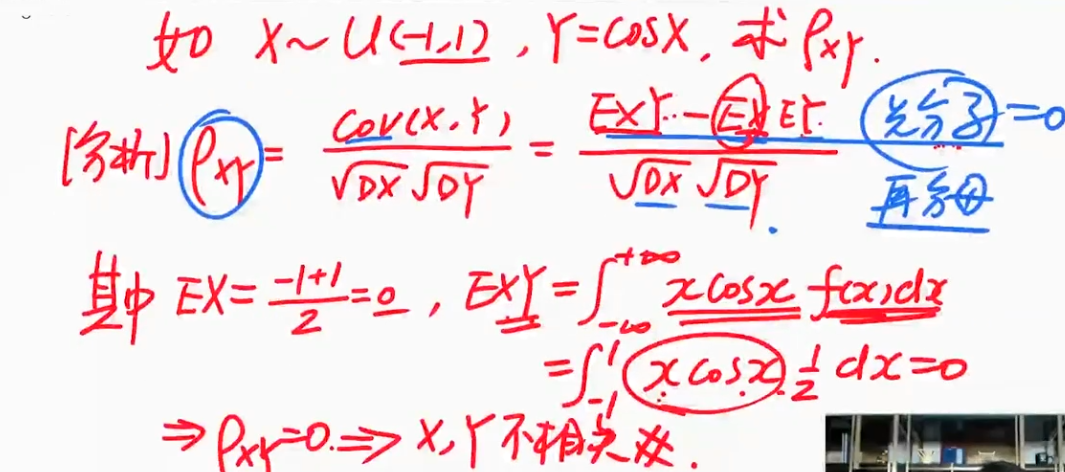 | 一道例题 先算分子,再算分母 用函数的奇偶性 |
相关性是描述线性相关性
性质
| 图片 | 要点 |
|---|---|
 | 协方差的综合 |
自己与自己的协方差是方差
独立性与相关性的判定
- 不相关也能证明独立性
- 独立:有纠缠关系
- 相关性:有线性相关关系
独立必定不相关
二维正态分布,X,Y独立$\iff$X,Y相关
相关必定不独立
| 图片 | 要点 |
|---|---|
 | 做题程序 |
用分布判定独立性
用数字特征判定相关性
大数定律与中心极限定理
p515
不会出大题,一般是5分
依概率收敛
依概率收敛

| 图片 | 要点 |
|---|---|
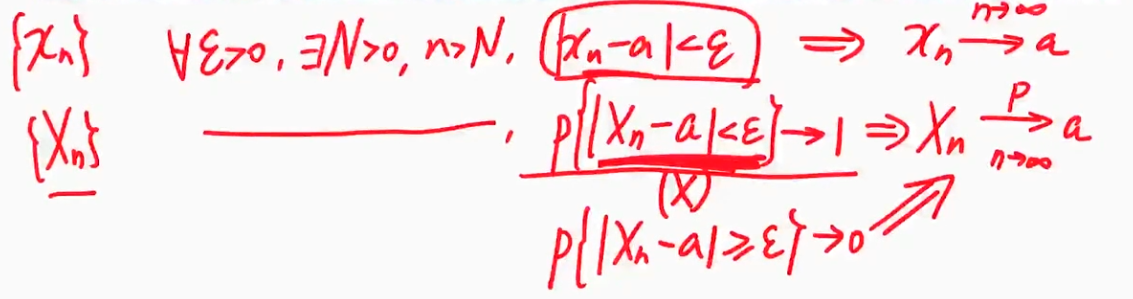 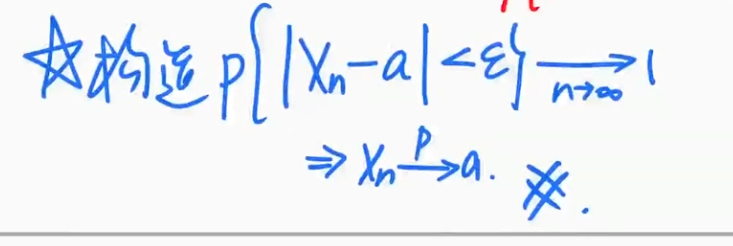 | 联系高等数学的收敛 构造一个形式 |
大数定律
满足一定的条件下,所有的大数定律为(均值趋于稳定):
$$
\dfrac{1}{n} \displaystyle \sum_{i=1}^nx_i \quad \underrightarrow{P} \quad E(\dfrac{1}{n} \displaystyle \sum_{i=1}^nx_i) = \text{数}
$$
大数定律告诉我们能用频率近似代替概率;能用样本均值近似代替总体均值。
总结来看,大数定理将属于数理统计的平均值和属于概率论的期望联系在了一起。
大数定理的总结
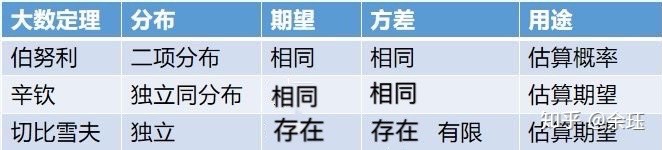
辛钦大数定律不是只要求独立同分布期望存在就可以了吗,为什么最下面里有方差相同呢,方差不一定存在怎么来的相同呢
他是不是把辛钦大数定律和切比雪夫大数定理弄反啦
切比雪夫大数定律
条件:
- 相互独立
- 方差存在
$\color{green}{\text{直觉:样本均值约等于总体均值}}$
伯努利大数定律
$\color{green}{\text{直觉:样本概率约等于总体概率}}$
辛钦大数定律
条件:
- 独立
- 同分布
- 期望存在
故伯努利大数定律是辛钦伯努利大数定律的一个特例。
中心极限定理
中心极限定理均为:
$\text{若}x_i$ $\buildrel \rm iid(\text{独立同分布,identically distributed})\over{\backsim}$ $F,EX_i=\mu,DX_i=\sigma^2$
$\text{则} \displaystyle \sum_{i=1}^nx_i$ $\buildrel \rm x \to \infty \over{\backsim}$ $N(n\mu,n\sigma)(\text{正态分布})$
$\text{且} \dfrac{\displaystyle \sum_{i=1}^nx_i - n\mu}{\sqrt{n}\sigma}$ $\buildrel \rm x \to \infty \over{\backsim}$ $N(0,1)(\text{标准正太分布})$
中心极限定理说明样本的均值在总体均值的周围
列维-林德伯格定理
列维-林德伯格定理

棣莫弗-拉普拉斯定理
棣莫弗-拉普拉斯定理

数理统计
p520
$\bigstar$ $\bigstar$ $\bigstar$ 第一遍的时候好多题都没懂,其实是因为公式不清晰
下面的公式是数理统计的基础
| 公式 | 记忆方法 |
|---|---|
| $E(\bar{X})=\mu$ | 样本的平均值期望将会收敛到整体的均值 |
| $D(\bar{X})=\dfrac{\sigma^2}{n}$ | 样本的期望将会收敛到整体的均值得: 方差随着n的增大会变成0,即样本的值也会收敛到均值 |
| $E(S^2)=\sigma^2$ | 样本方差的期望就是方差 |
| $D(X)=E(X^2)-\lbrack E(X)\rbrack^2$ | 内的强大,永远比外的强大,更强大(平方在外在内) 内外能力值的差,就是你能力的波动性(二者相减就是方差) |
回头看了看之前不太懂的$D(X)=E(X^2)-\lbrack E(X)\rbrack^2$推导,发现数学语言和程序语言类似只要把握几个点
- 命名空间
- 参数类型
- 返回值类型
总体与样本
总体定义
研究对象的全体称为总体,组成总体的每一个元素称为个体.
样本
简单随机样本,简称样本.
$x_i$ $\buildrel \rm iid(\text{独立同分布,identically distributed})\over{\backsim}$ $X$
定义
分布
统计量及其分布
统计量
统计量的观测值
统计量

定义
常用统计量
补充结论
$D \bar{X} = \dfrac{\sigma^2}{n}$
$E \bar{S^2} = \sigma^2$
样本均值
样本方差
为什么是$n-1$,有证明,是修正之后的系数
样本标准差
样本k阶(原点)矩
样本k阶中心矩
顺序统计量
图片详情

联系第三讲p477
| 图片 | 要点 |
|---|---|
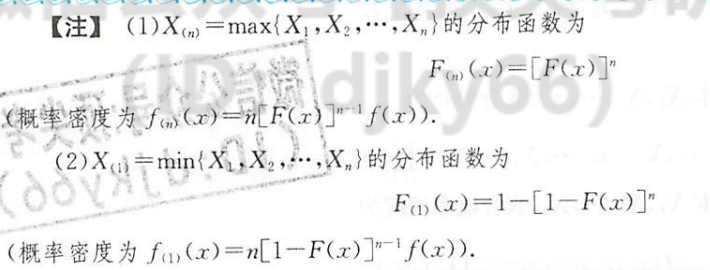 | 最大最小值独立同分布的概率密度 |
性质
最后一个推导有讲解,也有要求掌握
三大分布
5分
$\chi^2$分布
$\chi^2$分布的定义
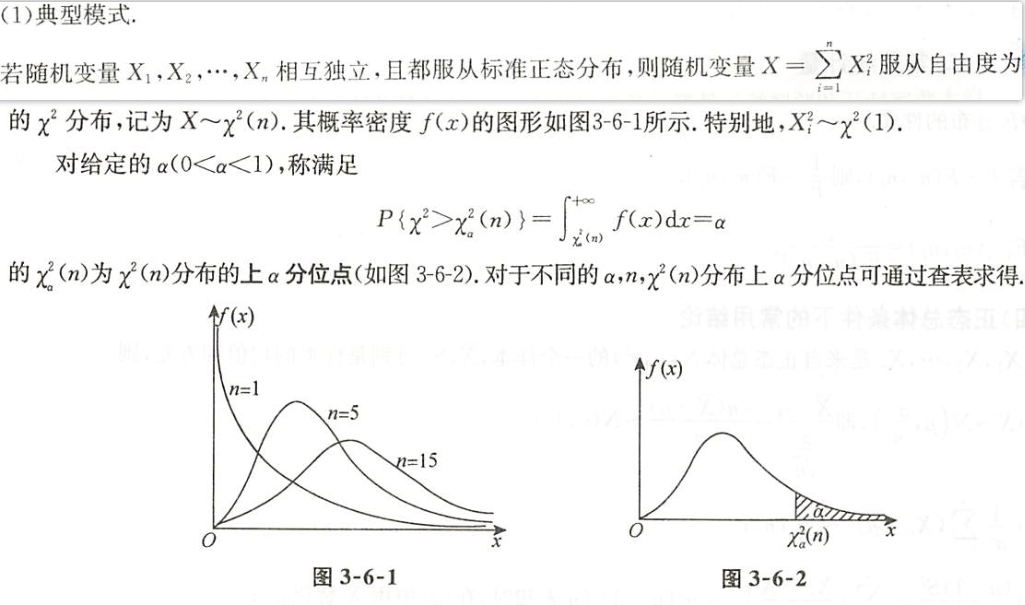
| 图片 | 要点 |
|---|---|
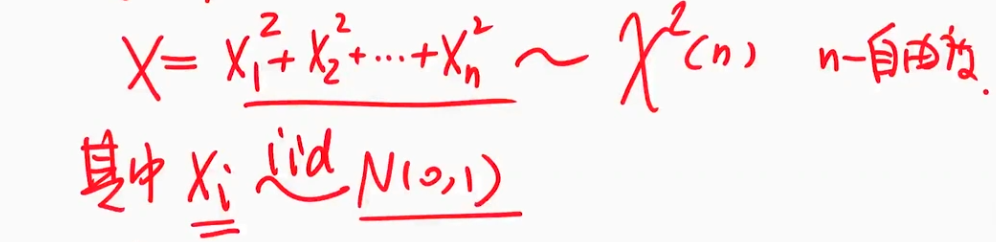 | 卡方分布的定义 |
卡方分布具有可加性
$t$分布
$\sharp$ 学生分布
$t$分布的定义和图像

| 图片 | 要点 |
|---|---|
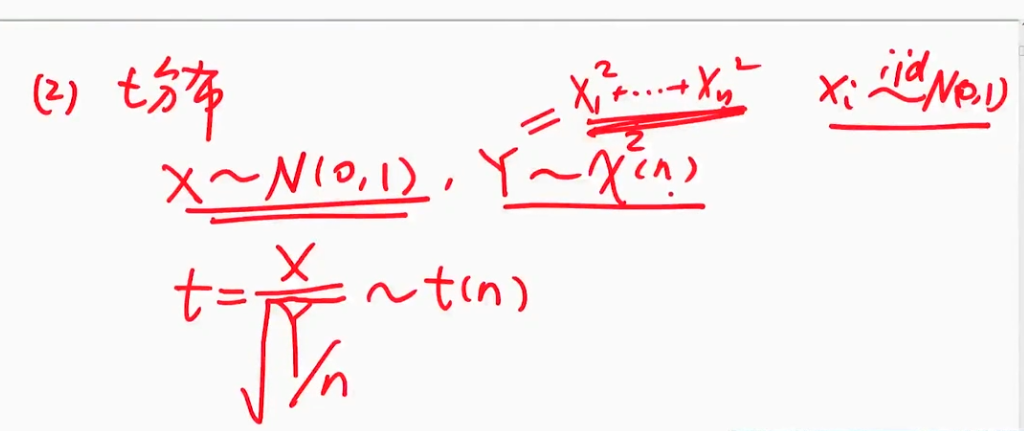 | t分布的定义 |
| 图片 | 要点 |
|---|---|
| $-t_\alpha(n)=t_{1-\alpha}(n)$ | 选择题的小知识 例3.6.17 |
$F$分布
$F$分布的定义和图像

| 图片 | 要点 |
|---|---|
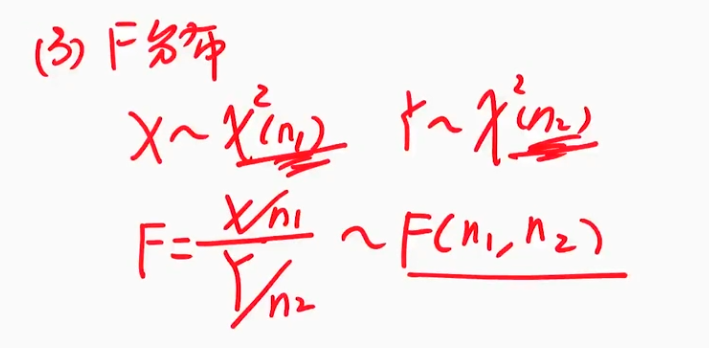 | 定义 记忆方法:两个X最后和合成F(inal)分布 |
| 图片 | 要点 |
|---|---|
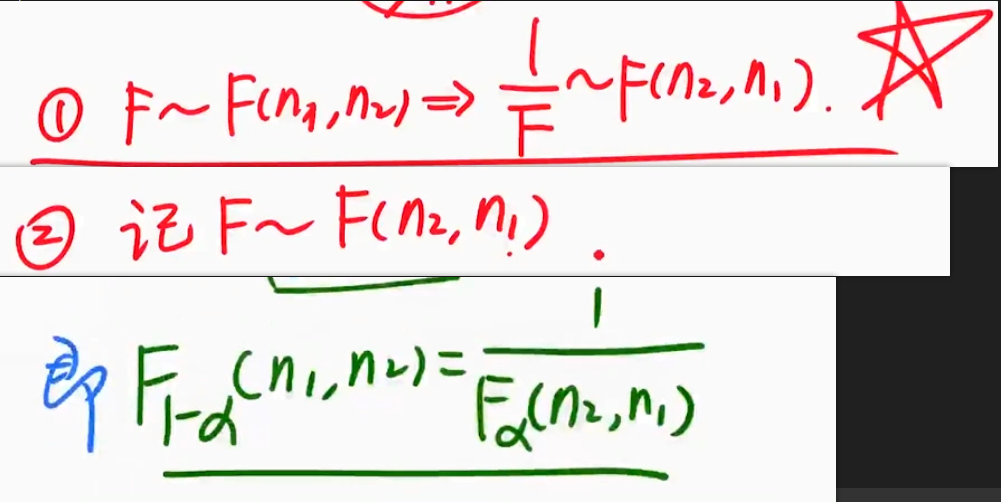 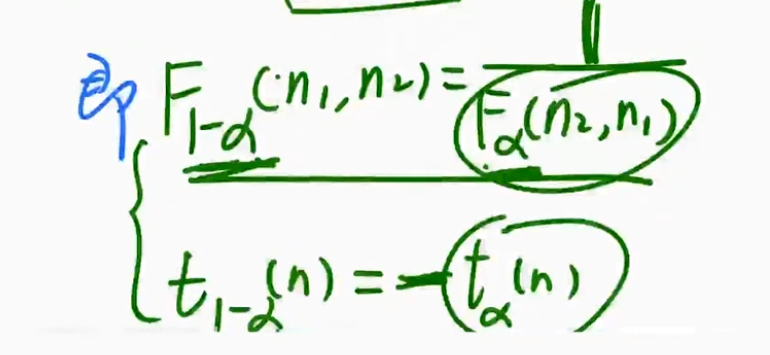 | 需要记住的性质知识点 |
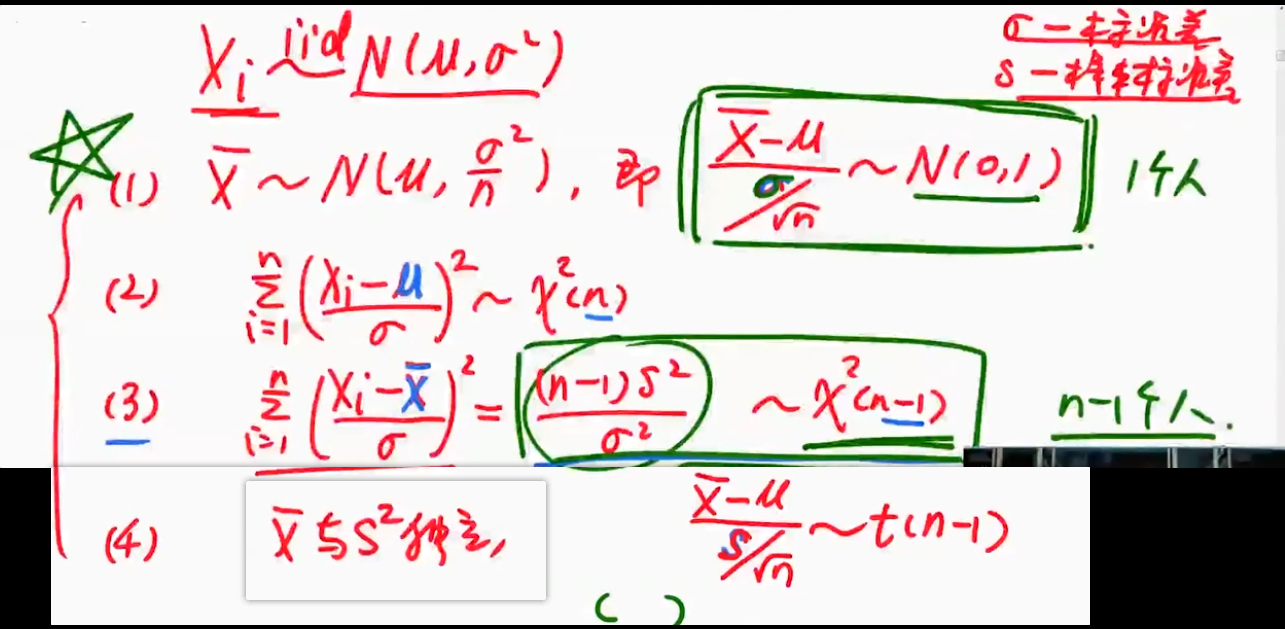
正态总体下的常用结论
正态总体下的常用结论

p471
在学校教材,浙江大学的教材《概率论与数理统计》的第四版的p142(平方的期望(方差的变体式)参考了p101页):
- $E(\bar{X})=\mu,\quad D(\bar{X})=\dfrac{\sigma^2}{n}$
- $E(S^2)=E\lbrack \dfrac{1}{n-1}(\displaystyle \sum_{i=1}^nX_i^2-n\bar{X}^2) \rbrack(\text{样本方差的定义式})=\dfrac{1}{n-1}\lbrack \displaystyle \sum_{i=1}^nE(X_i^2)-nE(\bar{X}^2) \rbrack(\text{样本方差的推导式})=\dfrac{1}{n-1}\lbrack \displaystyle \sum_{i=1}^n(\sigma^2 + \mu^2) -n(\dfrac{\sigma^2}{n}+\mu^2)\rbrack(方差的变体式)=\sigma^2$
参数的点估计
14分
概念
图片详情

方法
矩估计法
图片详情

最大似然估计法
将概率乘起来然后再求导
最大似然的基本思想

最大似然估计量的步骤

最大似然的不变性原则

估计量的评价标准(仅数学一要求)
无偏性
图片详情

有效性(最小方差性)
图片详情
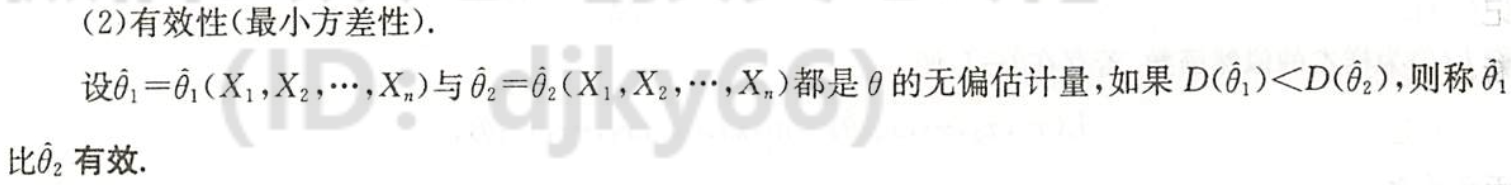
一致性(相合性)
图片详情

参数的区间估计与假设检验(仅数学一要求)
5分
| 图片 | 要点 |
|---|---|
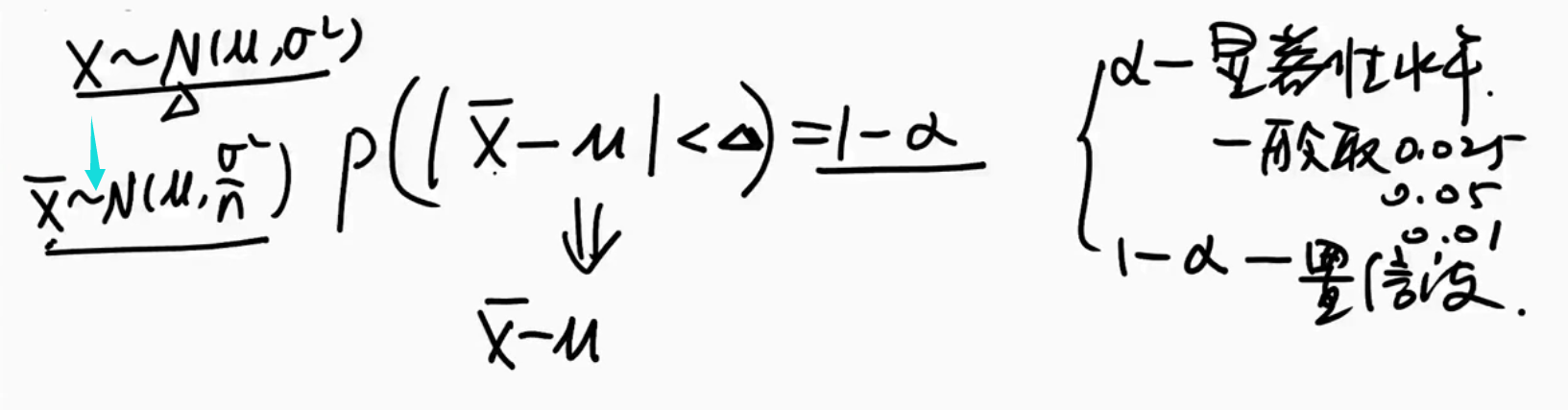 | 青色的箭头怎么来的 |
区间估计
概念
图片详情

正态总体均值的置信区间(置信水平为$1-\alpha$)
正态总体均值的置信区间(置信水平为$1-\alpha$)

假设检验
思想方法
图片详情

正态总体下的六大检验及拒绝域
图片详情

两类错误
图片详情