zy2022
线性代数
二次型
p407
二次型的定义与矩阵表示
二次型可以写为矩阵相乘的形式,$\mathbf{A}$为$f$的二次型矩阵,且$\mathbf{A}$是实对称矩阵
$f=X^T\mathbf{A}X$
写二次型矩阵的方法是$\mathbf{A}$的主对角线元素 $a_{ii}$ 是 $x_{i}^2$ 的系数, $a_{ij}$ 是 $x_i x_j$ 的系数一半
二次型矩阵是 $\color{green}{\text{对称矩阵}}$
图片详情

化二次型为标准形与规范形
二次型为标准形与规范形的定义
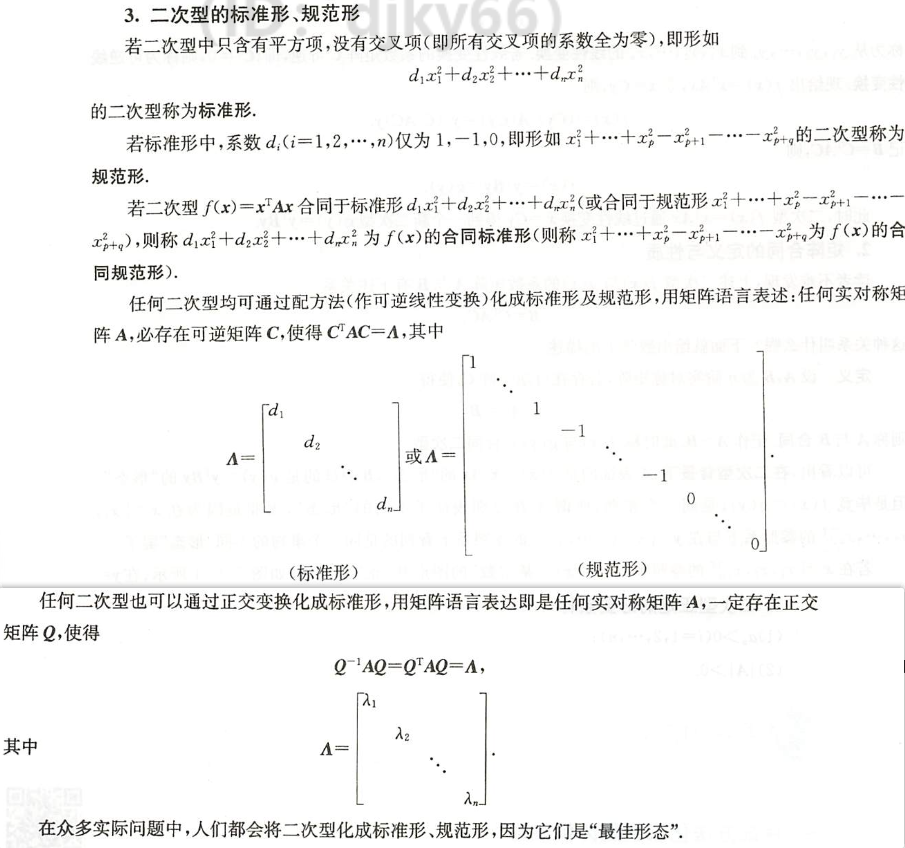
- 二次型的 $\color{green}{\text{标准形}}$ : 只含有完全平方项的二次型
二次型的标准形的定义
- 核心内容
- 联系p408
变换就是高等数学里面的换元
合同变换线性变换是可逆的变换就是合同变换
能够直接看出最大最小值的形状就是标准型,规范型
配方法
任何二次型均可通过配方法(作可逆线性变换)化成标准形及规范形,
二次型中含有完全平方项情形
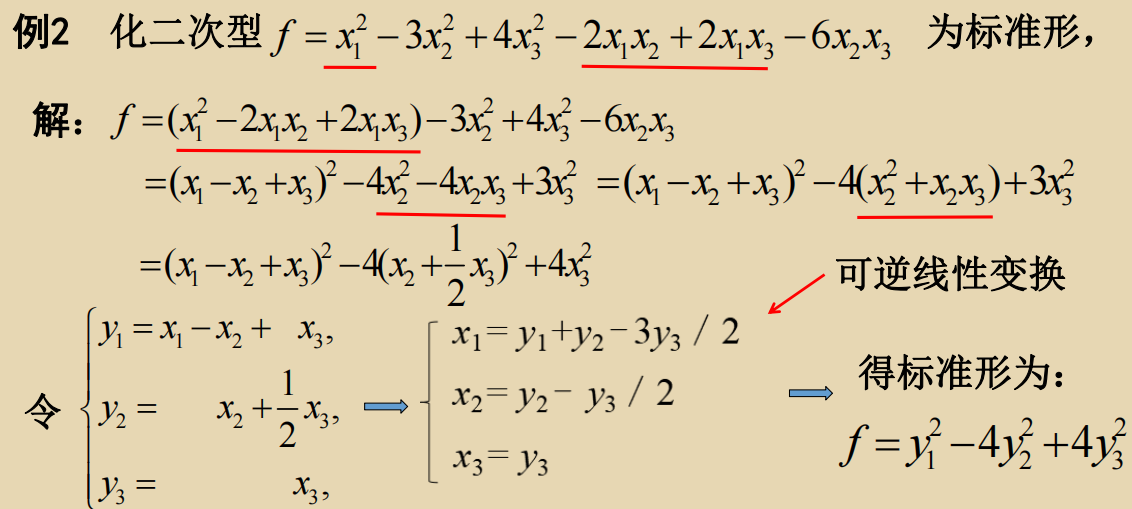
二次型中不含有完全平方项情形

正交变换法
任何二次型也可以通过正交变换化成标准形
图片详情

合同
图片详情

合同的充要条件是有相同的正,负惯性指数
合同的性质

惯性定理
标准型里面, $\color{green}{\text{正项}}$ 个数$p$与 $\color{green}{\text{负项}}$ $q$个数都是不变的,$p$称为正惯性指数,$q$称为负惯性指数
正定二次型
正惯性指数为n
二次型的前提是对称矩阵,讨论合同的前提是对称矩阵($\mathbf{A}^T=\mathbf{A}$)
定义
正定二次型的定义

充要条件
正定二次型的充要条件

必要条件
正定二次型的必要条件

判定
具体型二次型
选择题用主子式可能更快

抽象型二次型
- ${\textstyle\unicode{x2460}}$ 说对称
- ${\textstyle\unicode{x2461}}$ 说$\lambda$ 特征值全是0



