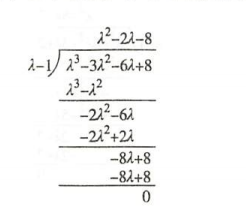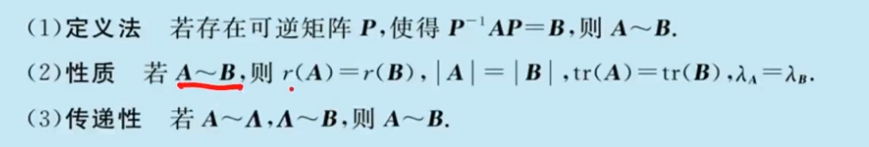zy2022
线性代数
特征值与特征向量
p379
此讲的矩阵均为方阵
总结一下每一讲对形状的限制
1.行列式,一定是方阵 $\mathbf{A}_{n\times n}$
2.矩阵,没有限定形状,$\mathbf{A}_{m \times n}$
3.向量组,没有限定形状,$\mathbf{A}_{m \times n}$
4.方程组,没有限定形状,$\mathbf{A}_{m \times n}$
5.特征值,一定是方阵 $\mathbf{A}_{n\times n}$
6.二次型,一定是方阵 $\mathbf{A}_{n\times n}$
特征值与特征向量
定义
定义

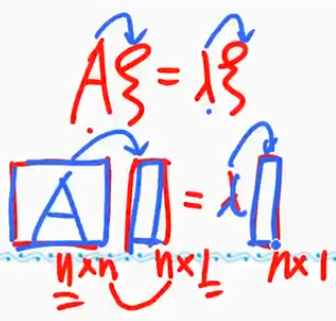
$\mathbf{A}\mathbf{\xi}=\lambda \mathbf{\xi}$
$\mathbf{\xi}$是$\mathbf{A}$的特征值,$\mathbf{\xi}$是$\mathbf{A}$的特征向量
$|\lambda \mathbf{E}- \mathbf{A}|=0$特征方程
性质
上下三角矩阵与对角矩阵的特征值就是对角线元素
特征值的性质
特征值加起来等于迹$tr(\mathbf{A})$
特征值乘起来等于行列式的值
特征向量的性质
(1) $k$重特征值$\lambda$至多只有$k$个线性无关的特征向量(直接使用无需证明)(例2.5.1)
(2) 若$\xi_1,\xi_2$是$\mathbf{A}$属于不同特征值的特征向量,则$\xi_1,\xi_2$线性无关(例2.5.5)
(3) 若$\xi_1,\xi_2$是$\mathbf{A}$属于同一特征值的特征向量,则$k_1\xi_1+k_2\xi_2$仍是$\mathbf{A}$属于特征值$\lambda$的特征向量(例2.5.7)
常用矩阵的特征值和特征向量
常用矩阵的特征值和特征向量

求法
具体型矩阵
注:不能有0解,不同时为0
提出法
试根法(试-1,1,0,最高次项的系数是1:试0次项的因子)
- $\bigstar$ $\bigstar$ $\bigstar$ 多项式的带余除法(顶级方法)
抽象型矩阵
证明主要是用定义- $\bigstar$(A不是必定不可以求逆吗,A的行列式必须是0?) 答:特征方程不是A
- 最后一个的证明,塞到矩阵中间的一定是$\mathbf{E}$
- $\mathbf{A}^T$特征值不变,特征向量不知道
相似
矩阵相似
定义
图片详情

性质
相似矩阵的性质

- 秩,行列式,特征方程 ,特征值相同,迹相同
- 对应的的矩阵多项式和矩阵的幂也相似
- 对应的逆矩阵也相似
- 对应的转置也相似
- A的伴随和B的伴随也相似
两个矩阵是否相似的判别与证明
两个矩阵是否相似的判别与证明

矩阵的相似对角化
- 回答为什么要求特征值和特征向量
能否相似对角化的例题1

能否相似对角化的例题2

定义
$\mathbf{P}^{-1}\mathbf{A}\mathbf{P}=\mathbf{\Lambda}$,$\mathbf{\Lambda}$为对角矩阵,则称$\mathbf{A}$可相似对角化,$\mathbf{\Lambda}$是$\mathbf{A}$的相似标准型
矩阵的相似对角化的定义
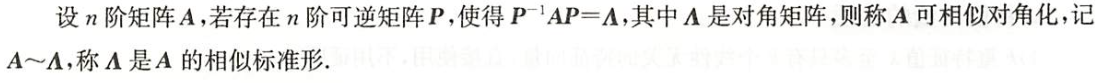
可相似对角化的条件
充分必要条件:$\mathbf{A}$有$n$个线性无关的特征向量
注:特征值与特征向量线性相关的关系
$$
\begin{cases}
\text{普通} \mathbf{A} \begin{cases}
\lambda_1 \neq \lambda_2 \implies \xi_1 \text{与} \xi_2 \text{无关} (\text{例2.5.5})\cr \cr
\lambda_1 = \lambda_2 \implies \begin{cases}
\xi_1 \text{与} \xi_2 \text{相关}(\text{例2.5.10(D)}) \cr \cr
\xi_1 \text{与} \xi_2 \text{无关} (\text{例2.5.10(C)})
\end{cases} \cr \cr
\end{cases} \cr \cr
\text{实际对称} \mathbf{A}\text{((必可相似对角化))}\begin{cases}
\lambda_1 \neq \lambda_2 \implies \xi_1 \perp \xi_2 (\text{例2.5.16})\cr \cr
\lambda_1 = \lambda_2 \implies \begin{cases}
\xi_1 \perp \xi_2 \cr \cr
\xi_1 \text{与} \xi_2 \text{无关}
\end{cases} \cr \cr
\end{cases}
\end{cases}
$$
两个充分
两个必要
实对称矩阵必可相似于对角阵

相似对角化的步骤
(1) 求$\mathbf{A}$的$\lambda$
(2) 求$\mathbf{A}$的$\lambda$的$\xi$
(3)令$P=(\xi_1\cdots \xi_2)$
应用
实对称矩阵的相似对角化
(1)$\mathbf{A}$是实对称矩阵,则$\mathbf{A}$的特征值是实数﹐特征向量是实向量(不用证)
(2)实对称矩阵$\mathbf{A}$的属于不同特征值的特征向量相互正交(证明见例2.5.16).
(3)实是对称矩阵的$\mathbf{P}$可以变换(正交化单位化)为正交矩阵
反问题
反求参数
反求参数的三种方法
反求$\mathbf{A}$
反求矩阵
$$
\begin{cases}
{\textstyle\unicode{x2460}} \mathbf{A}=\mathbf{P} \Lambda \mathbf{P}^{-1},(例2.5.21) & \cr
\bigstar {\textstyle\unicode{x2461}} \mathbf{A}^k=\mathbf{P} \Lambda^k \mathbf{P}^{-1} , & \cr
\bigstar {\textstyle\unicode{x2462}} f(\mathbf{A})=\mathbf{P} f(\Lambda) \mathbf{P}^{-1} , & \cr
\end{cases}
$$