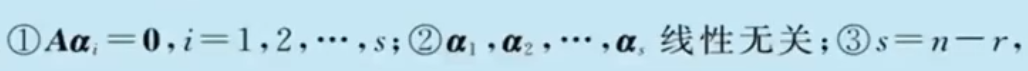zy2022
线性代数
线性方程组
p360
最主要的任务是求解
2021考了12分
增广矩阵
具体型线性方程组
齐次
- 齐次方程组必有零解
有解条件
当$r(\mathbf{A})=n$时,齐次方程组有唯一零解
当$r(\mathbf{A})=r<n$时,齐次方程组有非零解(有无穷多个解),且有$n-r$个线性无关解
- r是独立方程个数
解的性质
图片详情
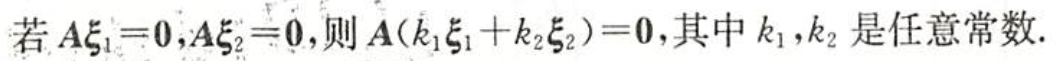
$\bigstar$ 基础解系和解的结构
- 是方程组$\mathbf{A}\mathbf{x}=\mathbf{0}$的解
- 线性无关
- 方程组任意一解可以由基础解系线性表出
求解方法与步骤
- 作初等行变换化为阶梯型矩阵
- 按列找出一个秩为$r$的子矩阵,则剩余列位置的未知数即设为自由变量
- 按基础解系的定义写出通解
$\sharp$ 拓展:为什么只能做初等行变换,做初等列变换的时候会发生什么
求解方法与步骤(学校课件)

非齐次
- $\mathbf{b}$能不能线性表出的问题
有解条件
$$
r(\mathbf{A})=r(\mathbf{A}|\mathbf{b}) \begin{cases}
=n \quad \text{唯一解} , & \cr
<n \quad \text{无穷多解} , &
\end{cases} \
r(\mathbf{A}) + 1=r(\mathbf{A}|\mathbf{b}) \quad \text{无解}
$$
图片详情

解的性质
图片详情

求解方法与步骤
非齐次的通解=齐次的通解+非齐次的一个特解
图片详情

抽象型线性方程组
有解条件与解的判定
两道例题

解的结构
理论依据

例题

基础解系的讨论
- 三个条件
例题

例题2

系数矩阵列向量与解的关系
- 方程组的解就是描述向量组中各向量之间数量关系的系数
理论依据

图片详情

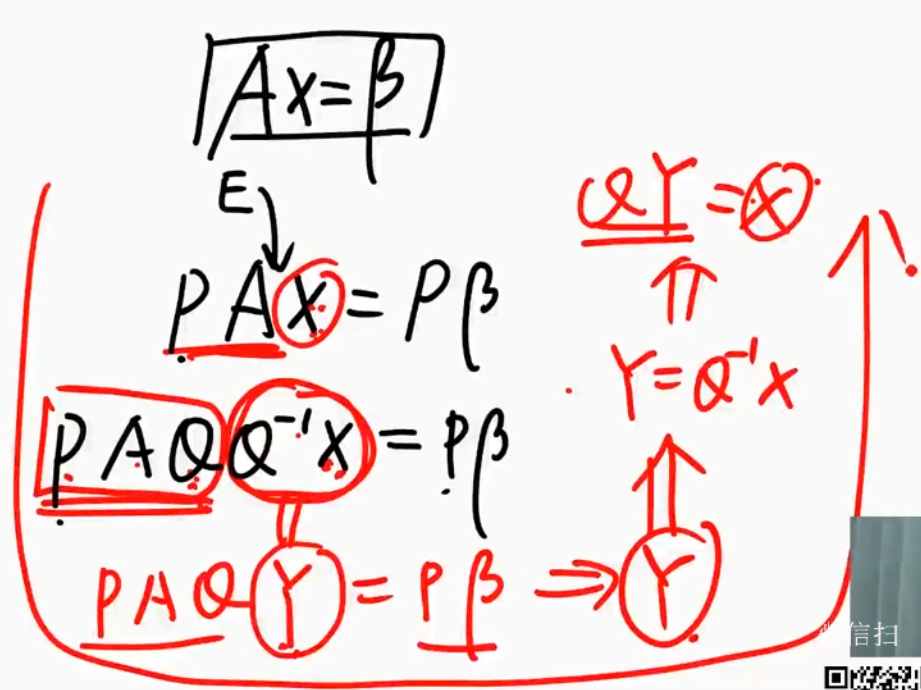
两个方程组的公共解
- 联立两个方程组求解即可
- 求出关系,代回通解
- 令两个基础解系相等
理论依据

题目

法一
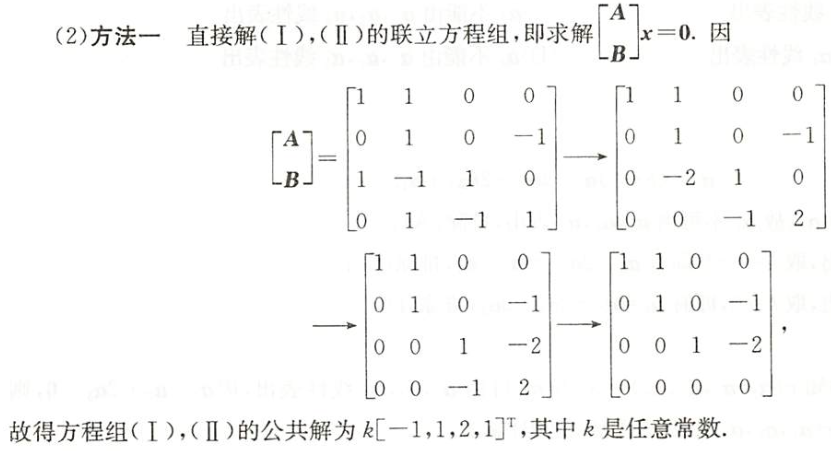
法二

法三

同解方程组
- 通解要求解全相等
- 公共解只是两个解的交集
理论依据

两道例题