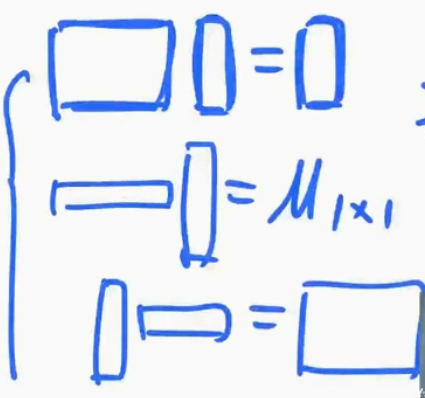zy2022
线性代数
向量组
p341
线性代数的主人翁
熟悉矩阵相乘的形状
向量与向量组的线性相关性
如何判断向量组是线性相关的
- 按照定义如果能够线性凑一个等式,系数不全为0,那么线性相关
- 凑成两个矩阵的乘积取行列式,值不为0,则线性无关
向量定义
向量定义图片详情

线性组合
n个向量的线性组合
$\bigstar$ 线性表出
- 与非齐次方程组的解$\mathbf{A}x=\beta$联系
线性表出的定义
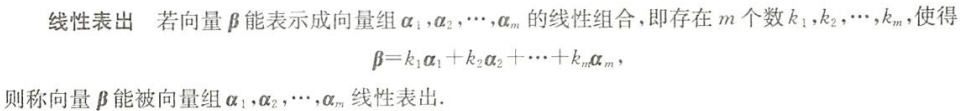
能表出
不能表出
$\bigstar$ 线性相关性
- 与齐次方程组的解$\mathbf{A}x=0$联系
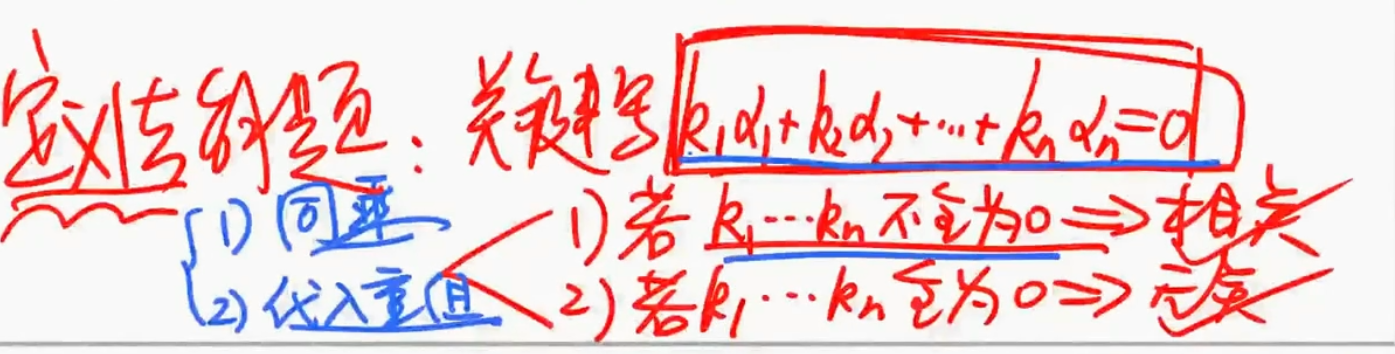
用线性相关性的定义解题
线性相关的定义

相关
含有零向量或有成比例的向量的向量组必线性相关.
如果只有一个向量且线性相关,这个向量是0向量
无关
n个向量线性相加得0,所有向量前面的系数都是0
判别的七大定理
定理1 向量组线性相关,其中一个向量可以由剩余的向量线性表示
图片详情

定理2 $\mathbf{\alpha}$之间线性无关,来了个$\mathbf{\beta}$线性相关,$\mathbf{\beta}$可以由$\mathbf{\alpha}$们线性表示
- 证明基本上都是定义法
图片详情

定理3 以少表多,多的线性相关
以少表多,多的线性相关

定理4:向量组线性相关的充分必要条件是齐次线性方程组$\mathbf{A}x=\mathbf{0}$有非零解
- 向量组中向量的维数小于个数(列数大于行数,形状横条),必然线性相关
- 向量组中向量的维数等于个数(行数等于列数,形状方形):行列式为0,线性相关;行列式不为0,线性无关
- 向量组中向量的维数大于个数(列数小于行数,竖条),1.先要化阶梯 2.
图片详情

图片详情

定理5 加一个线性相关的向量,秩不变
图片详情

定理6 部分相关,整体必相关
- 逆否命题成立。整体无关 $\implies$ 部分必无关
图片详情

定理7 原来无关 $\implies$ 延长无关
- 原来相关 $\implies$ 缩短相关(缩短其实应该是不一定的,万一把线性相关的都缩走了就不好了)
图片详情

极大线性无关组与向量组的秩
$\bigstar$ 极大无关组
- 极大线性无关:最简方程组
- 一个线性无关向量组的极大线性无关组就是向量本身
- 秩能表示极大线性无关组的个数
定义
图片详情

求法
求极大线性无关组的步骤
- 将向量组拼成矩阵$\mathbf{A}$,作初等行变换(在做同解变换),化为行阶梯矩阵,确定$r(\mathbf{A})$(向量组的秩)
- 按列找出一个秩为$r(\mathbf{A})$的子矩阵,即取为一个极大线性无关组
向量组的秩
- 向量组的秩,与矩阵的秩的关系:矩阵的秩就是它的行向量组(成或列向量组)的秩。(参考文献)
定义
图片详情
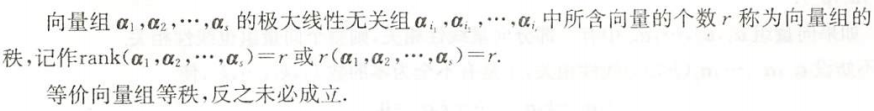
有关向量组的秩的重要定理和公式
被表出的秩不大
图片详情

$\bigstar$ 等价向量组
定义
两个向量组可以互相线性表出
向量组和他的极大线性无关组是等价的
判别
与等价矩阵的区别
等价矩阵和等价向量组的概念与区别
- 矩阵:$\mathbf{A},\mathbf{B}\text{同型}$:$\mathbf{A}\text{与}\mathbf{B}$等价$\iff r(\mathbf{A})=r(\mathbf{B})$ ($\mathbf{P}\mathbf{A}\mathbf{Q}=\mathbf{B}$)
- 等价向量组:$\mathrm{I}$,$\mathrm{II}$(同维即可) $\iff r(\mathrm{I})=r(\mathrm{II})=r(\mathrm{I|II})$
- 单方表出则互相表出
- $\blacktriangleright$(按照例2.3.14的说法,难道两个秩相等就能推出$r(\mathrm{I|II})$)
向量空间
概念
图片详情

基
坐标
维数
基变换与坐标变换
图片详情

变换公式
过渡矩阵
例题