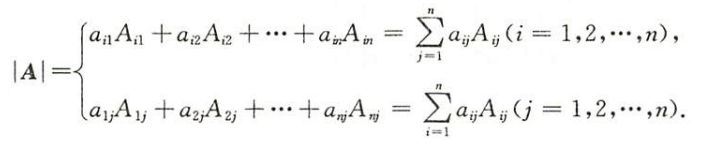zy2022
线性代数
行列式
p295
5分
只有方阵才能谈行列式
行列式的定义与性质
$a_{ij}$ i代表行号,j代表列号
主对角线,左上到右下;副对角线,右上到左下
行列式用字母$D$表示
本质定义(第一种定义)
- 2阶行列式是由两个2维向量(行向量)组成的,其(运算规则的)结果为以这两个向量为邻边的平行四边形的面积
- 3阶行列式其(运算规则的)结果为以这三个向量为邻边的平行六面体的体积.
- n阶行列式是由n个n维向量其(运算规则的)结果为以这n个向量为邻边的n维图形的体积.
- 由此看来,一个重要观点出现了:读者一开始,就应该把行列式看作是由若干个向量拼成的,并且要把这些向量作运算.
- 行列式线性无关,可以理解为行向量组成的图形面积不为0
- 行列式研究两个向量线性相关的一种工具
- 行列式算出来到底是几不重要,等不等于0才重要
性质
性质1 行列互换,其值不变,即 $|A|=|A^T|$.
性质2 行列式中某行(列)元素全为零,则行列式为零.(面积为0)
性质3 行列式中某行(列)元素有公因子k(k $\neq$ 0),则k可提到行列式外面
- 注意只乘进某一行去
- 用面积理解也好理解
- 倍乘
$$
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
ka_{i1} & ka_{i2} & \cdots & ka_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
= k
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
a_{i1} & a_{i2} & \cdots & a_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
$$
性质4 行列式中某行(列)元素均是两个元素之和,则可拆成两个行列式之和,
- 注意是$\color{red}{\text{单}}$行可加性
$$
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
a_{i1} + b_{i1} & a_{i2} + b_{i2} & \cdots & a_{in} + b_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
=
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
a_{i1} & a_{i2} & \cdots & a_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
+
\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
\vdots & \vdots& & \vdots \cr
b_{i1} & b_{i2} & \cdots & b_{in} \cr
\vdots & \vdots& & \vdots \cr
a_{n1}& a_{n2}& \cdots& a_{n3}
\end{vmatrix}
$$
性质5 行列式中两行(列)互换,行列式的值反号.
- 互换性质
性质6 行列式中的两行(列)元素相等或对应成比例,则行列式为零.
- 性质7和性质2可以推导性质6
性质7 行列式中某行(列)的k倍加到另一行(列),行列式的值不变.
- 倍加
初等变换
- 互换
- 倍乘
- 倍加
逆序数法定义(第二种定义)
- 可以用来检验
排列和逆序
排列:由n个数$1,2,\cdots,n$组成的一个有序数组称为一个n级排列,如23145是一个5级排列,41352也是一个5级排列.n级排列共有n!个.
逆序:一个n级排列$i_1i_2\cdots i_s\cdots i_t \cdots i_n$。中,若$i_s>i_t$,且$i_s$排在$i_t$,前面,则称这两个数构成一个逆序.
逆序数:一个排列中,逆序的总数称为该排列的逆序数,记作 $\tau(i_1i_2\cdots i_n)$,如$\tau$(231546)=3,$\tau$(621534)=8.由小到大顺排的排列称为自然排序,如12345,显然,自然排序的逆序数为0.
奇排列和偶排列:排列的逆序数为奇数时,该排列称为奇排列;排列的逆序数为偶数时,该排列称为偶排列.
n阶行列式的定义
取不同行不同列的乘积,行下标顺排,故为$n!$项和。当列下标为奇排列时,应附加负号;当列下标为偶排列时,应附加正号.
- 用来求给定展开项的正负号
展开定理(第三种定义)
$\bigstar$ $\bigstar$ $\bigstar$
余子式
$$\text{在}n\text{阶行列式中,去掉元素}a_{ij}\text{所在的第i行、第j列元素,}$$
$$\text{由剩下的元素按原来的位置与顺序组成的}n-1\text{阶行列式称为元素}a_{ij}\text{的余子式,记作}M_{ij}$$
代数余子式
$\bigstar$ $\bigstar$ $\bigstar$
$$
\text{余子式}M_{ij}\text{乘}(-1)^{i+j}\text{后称为}a_{ij}\text{的代数余子式,记作}A_{ij}\text{,即}
$$
$$
A_{ij}=(-1)^{i+j}M_{ij}
$$
行列式按某一行(列)展开的展开公式
行列式的值等于行列式的某行(列)元素分别乘其相应的代数余子式后再求和,即
但行列式的某行(列)元素分别乘另一行(列)元素的代数余子式后再求和,结果为零,即
几个重要的行列式
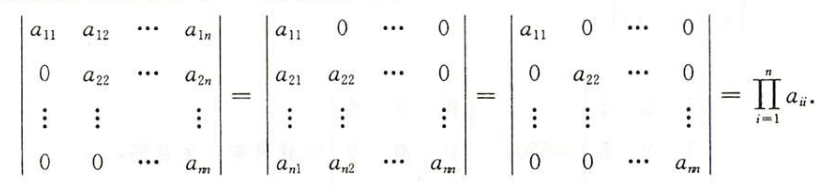
主对角线行列式
副对角线行列式
- 系数可以用逆序来理解
拉普拉斯展开式
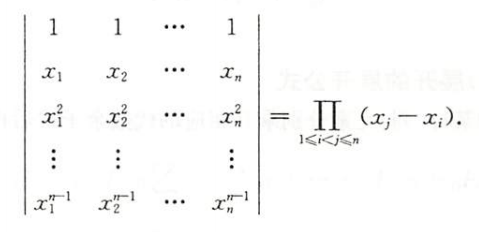
范德蒙德行列式
下标大的要把下标比他小的都减一遍再相乘
$\bigstar$ 行列式的计算
$\color{red}{\text{一句话总结}}$:${\textstyle\unicode{x2460}}$ 初等行变化,化成基本型,${\textstyle\unicode{x2461}}$递推
直接展开
- 0元素很多的情况
- 阶数不高的情况
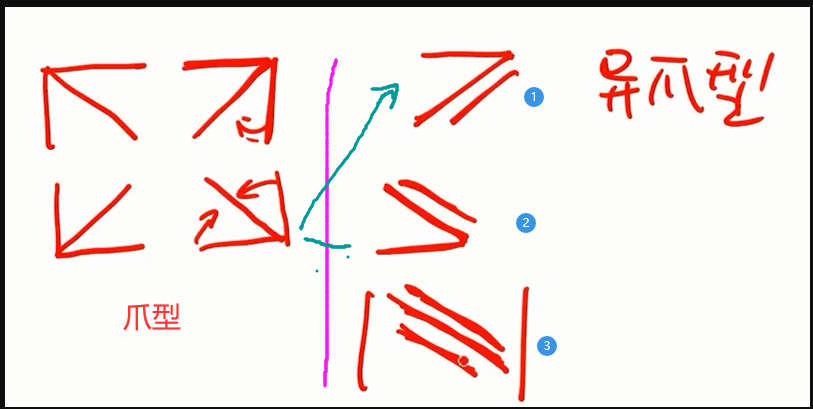
爪形
- 斜爪消平爪:依次提出斜爪上的值(倍乘性质),从第二行开始每一行依次去减第一行,就会变成主对角线行列式
异爪形
- 阶数低,直接展开:第${\textstyle\unicode{x2462}}$ 种 从最下面那一行开始展开比较好
- 阶数高,递推
- $\text{建立} D_n \text{与} D_{n-1} \text{的关系} \implies D_n $
- 找的$D_{n-1}$满足分布相同只是阶数降了一阶
行(列)和相等
- 加到第一行(列),提出去,在做初等变换(用第一行(列)去减下面的每一行)变成主对角行列式
消零化基本形
拉普拉斯展开:交换行列变成拉普拉斯展开
范德蒙德行列式
爪型vs异爪型
基本型指的是4个重要的行列式
具体型
化为基本型
递推法
行列式表示的函数和方程
抽象型
用性质
用公式$|AB|=|A||B|$
公式证明的参考文献
余子式与代数余子式的计算
$$
a_{ij}\text{的}A_{ij}(\text{代数余子式})\text{与}i,j(\text{的位置})\text{有关,与}a_{ij}\text{的大小无关}
$$