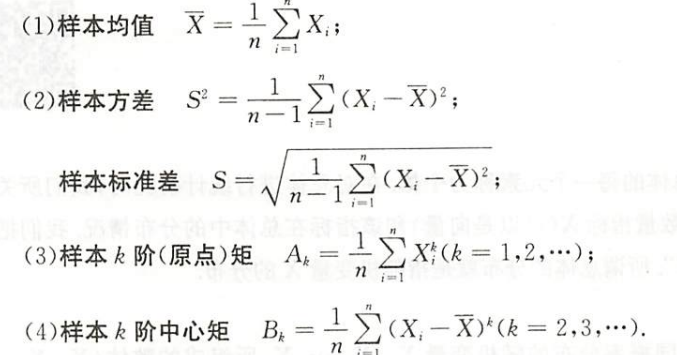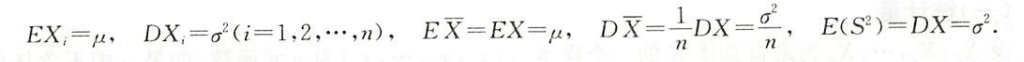zy2022
概率论与数理统计
数理统计
p520
$\bigstar$ $\bigstar$ $\bigstar$ 第一遍的时候好多题都没懂,其实是因为公式不清晰
下面的公式是数理统计的基础
| 公式 | 记忆方法 |
|---|---|
| $E(\bar{X})=\mu$ | 样本的平均值期望将会收敛到整体的均值 |
| $D(\bar{X})=\dfrac{\sigma^2}{n}$ | 样本的期望将会收敛到整体的均值得: 方差随着n的增大会变成0,即样本的值也会收敛到均值 |
| $E(S^2)=\sigma^2$ | 样本方差的期望就是方差 |
| $D(X)=E(X^2)-\lbrack E(X)\rbrack^2$ | 内的强大,永远比外的强大,更强大(平方在外在内) 内外能力值的差,就是你能力的波动性(二者相减就是方差) |
回头看了看之前不太懂的$D(X)=E(X^2)-\lbrack E(X)\rbrack^2$推导,发现数学语言和程序语言类似只要把握几个点
- 命名空间
- 参数类型
- 返回值类型
总体与样本
总体定义
研究对象的全体称为总体,组成总体的每一个元素称为个体.
样本
简单随机样本,简称样本.
$x_i$ $\buildrel \rm iid(\text{独立同分布,identically distributed})\over{\backsim}$ $X$
定义
分布
统计量及其分布
统计量
统计量的观测值
统计量

定义
常用统计量
补充结论
$D \bar{X} = \dfrac{\sigma^2}{n}$
$E \bar{S^2} = \sigma^2$
样本均值
样本方差
为什么是$n-1$,有证明,是修正之后的系数
样本标准差
样本k阶(原点)矩
样本k阶中心矩
顺序统计量
图片详情

联系第三讲p477
| 图片 | 要点 |
|---|---|
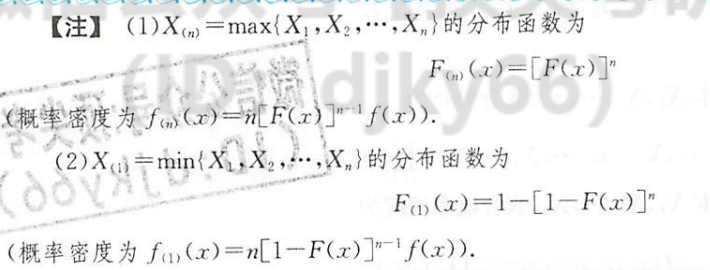 | 最大最小值独立同分布的概率密度 |
性质
最后一个推导有讲解,也有要求掌握
三大分布
5分
$\chi^2$分布
$\chi^2$分布的定义
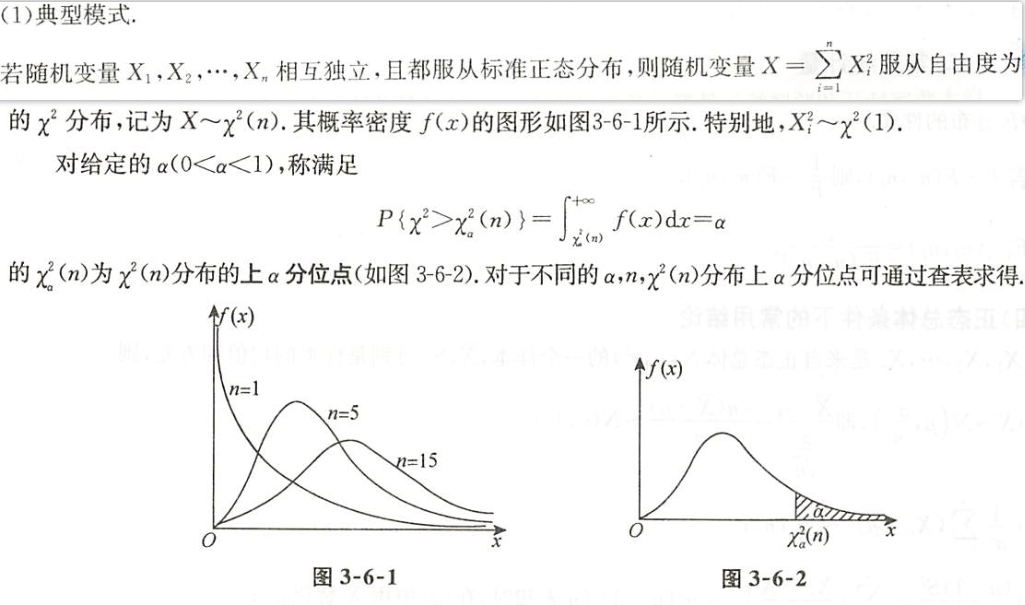
| 图片 | 要点 |
|---|---|
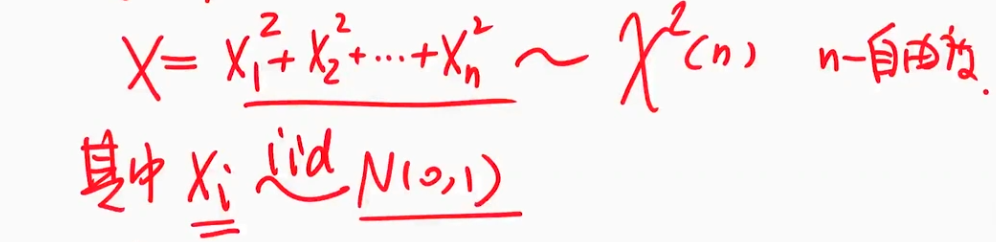 | 卡方分布的定义 |
卡方分布具有可加性
$t$分布
$\sharp$ 学生分布
$t$分布的定义和图像

| 图片 | 要点 |
|---|---|
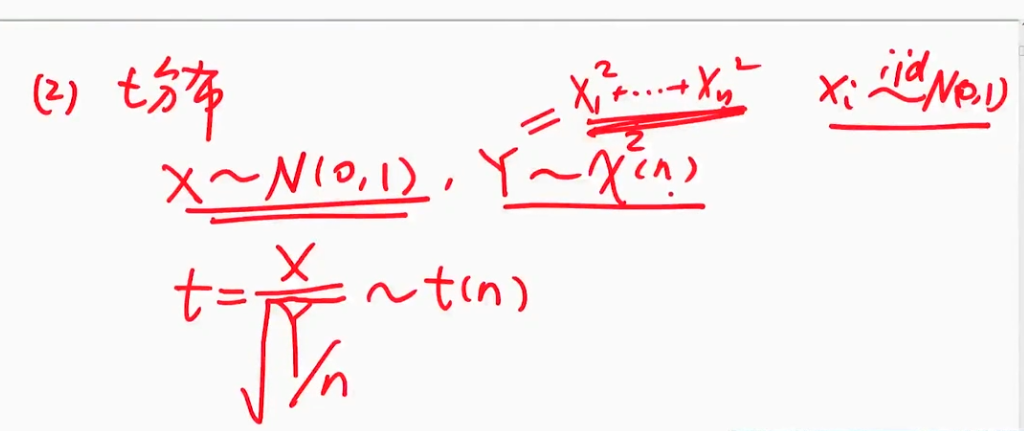 | t分布的定义 |
| 图片 | 要点 |
|---|---|
| $-t_\alpha(n)=t_{1-\alpha}(n)$ | 选择题的小知识 例3.6.17 |
$F$分布
$F$分布的定义和图像

| 图片 | 要点 |
|---|---|
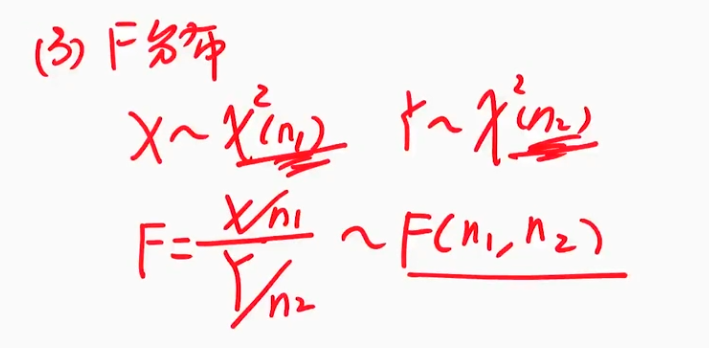 | 定义 记忆方法:两个X最后和合成F(inal)分布 |
| 图片 | 要点 |
|---|---|
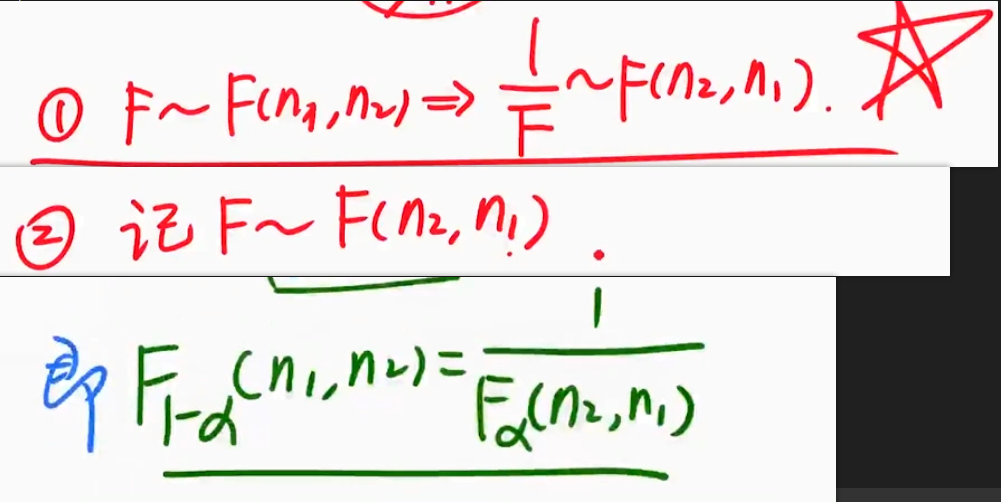 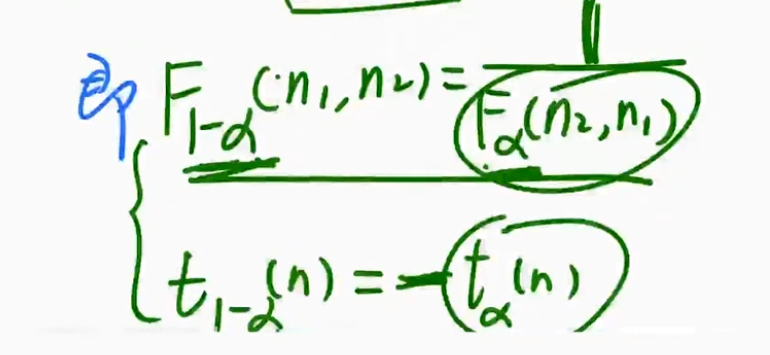 | 需要记住的性质知识点 |
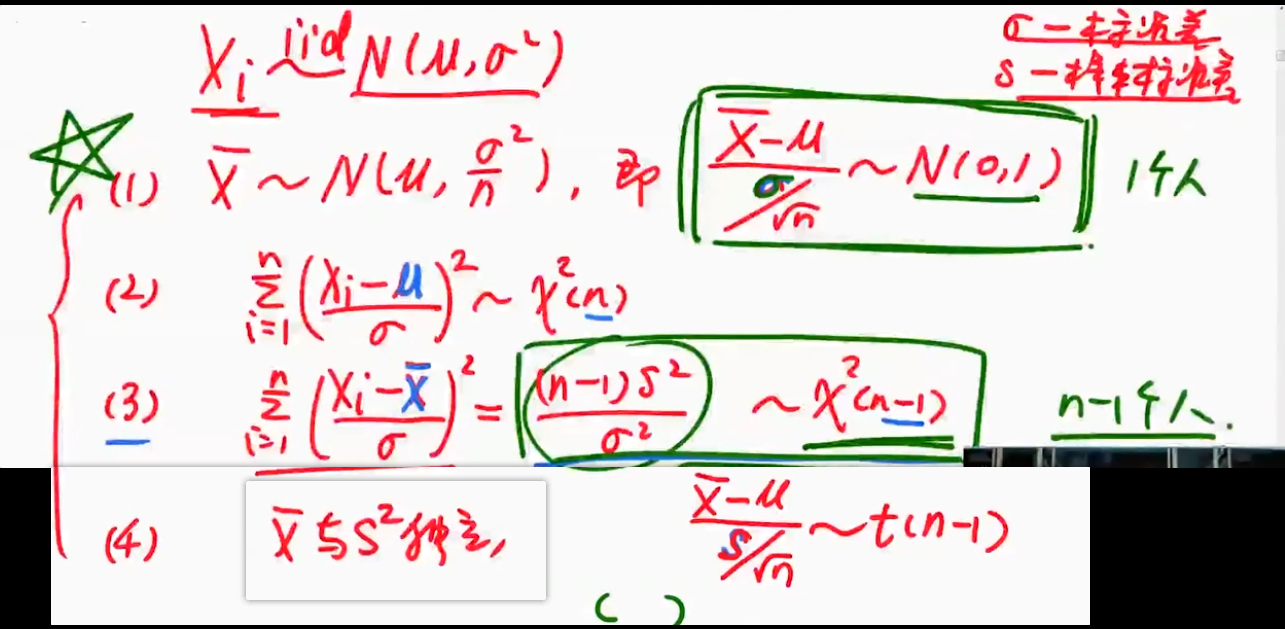
正态总体下的常用结论
正态总体下的常用结论

p471
在学校教材,浙江大学的教材《概率论与数理统计》的第四版的p142(平方的期望(方差的变体式)参考了p101页):
- $E(\bar{X})=\mu,\quad D(\bar{X})=\dfrac{\sigma^2}{n}$
- $E(S^2)=E\lbrack \dfrac{1}{n-1}(\displaystyle \sum_{i=1}^nX_i^2-n\bar{X}^2) \rbrack(\text{样本方差的定义式})=\dfrac{1}{n-1}\lbrack \displaystyle \sum_{i=1}^nE(X_i^2)-nE(\bar{X}^2) \rbrack(\text{样本方差的推导式})=\dfrac{1}{n-1}\lbrack \displaystyle \sum_{i=1}^n(\sigma^2 + \mu^2) -n(\dfrac{\sigma^2}{n}+\mu^2)\rbrack(方差的变体式)=\sigma^2$
参数的点估计
14分
概念
图片详情

方法
矩估计法
图片详情

最大似然估计法
将概率乘起来然后再求导
最大似然的基本思想

最大似然估计量的步骤

最大似然的不变性原则

估计量的评价标准(仅数学一要求)
无偏性
图片详情

有效性(最小方差性)
图片详情
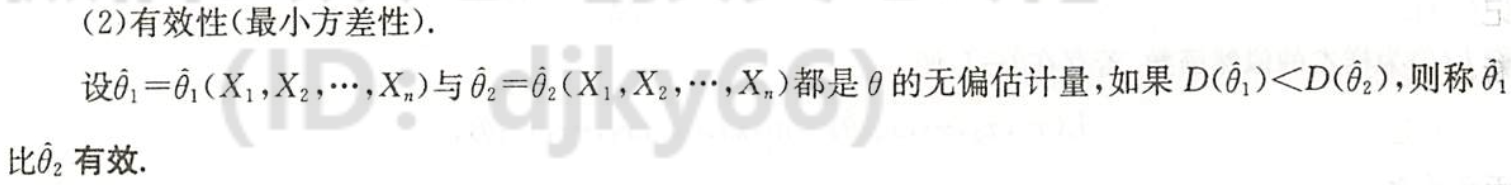
一致性(相合性)
图片详情

参数的区间估计与假设检验(仅数学一要求)
5分
| 图片 | 要点 |
|---|---|
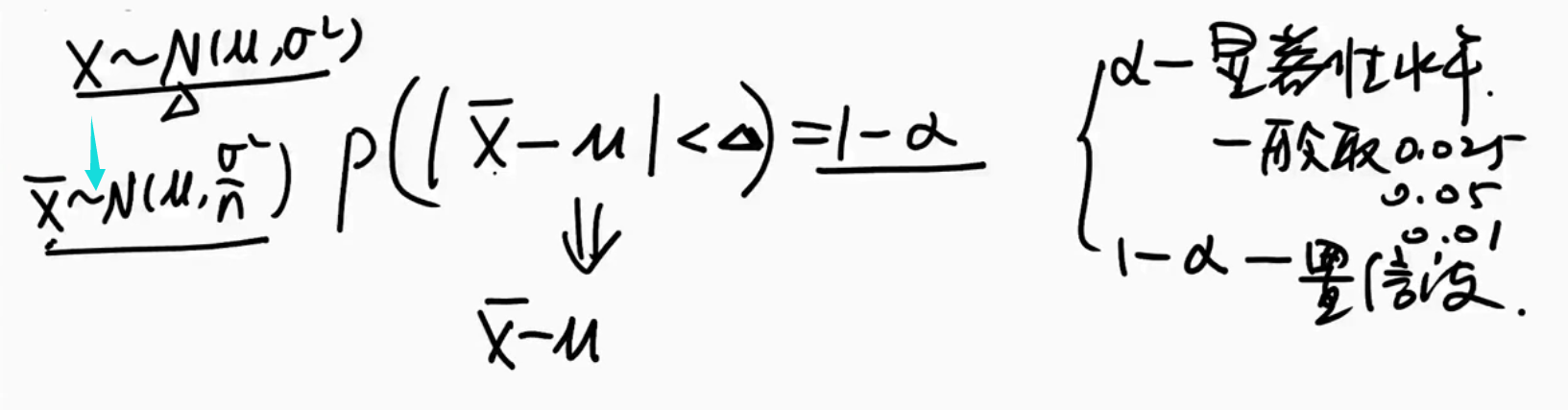 | 青色的箭头怎么来的 |
区间估计
概念
图片详情

正态总体均值的置信区间(置信水平为$1-\alpha$)
正态总体均值的置信区间(置信水平为$1-\alpha$)

假设检验
思想方法
图片详情

正态总体下的六大检验及拒绝域
图片详情

两类错误
图片详情