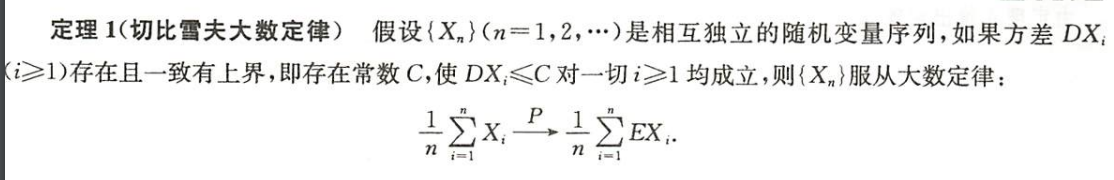zy2022

概率论与数理统计

大数定律与中心极限定理

p515

不会出大题，一般是5分

依概率收敛

图片	要点
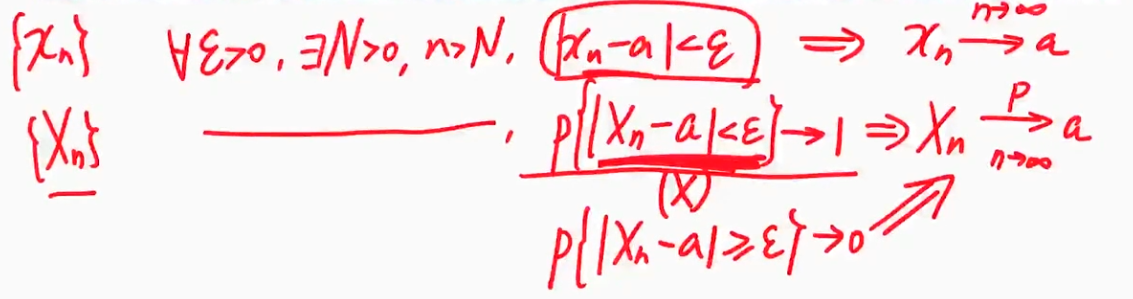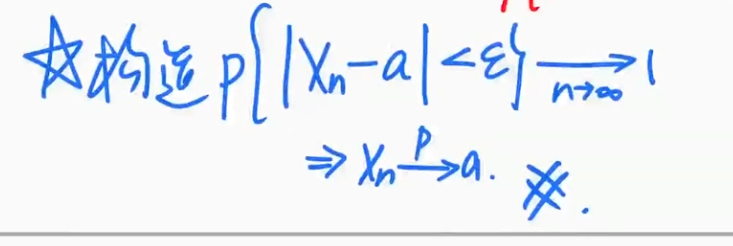	联系高等数学的收敛构造一个形式

大数定律

满足一定的条件下，所有的大数定律为(均值趋于稳定):
$$
\dfrac{1}{n} \displaystyle \sum_{i=1}^nx_i \quad \underrightarrow{P} \quad E(\dfrac{1}{n} \displaystyle \sum_{i=1}^nx_i) = \text{数}
$$

大数定律告诉我们能用频率近似代替概率；能用样本均值近似代替总体均值。

总结来看，大数定理将属于数理统计的平均值和属于概率论的期望联系在了一起。

大数定理的总结

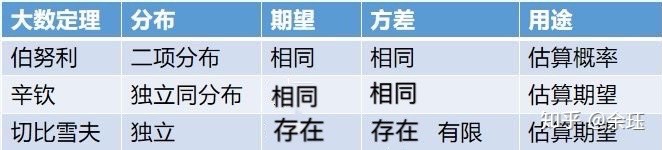
辛钦大数定律不是只要求独立同分布期望存在就可以了吗，为什么最下面里有方差相同呢，方差不一定存在怎么来的相同呢
他是不是把辛钦大数定律和切比雪夫大数定理弄反啦

切比雪夫大数定律

条件：

相互独立
方差存在

$\color{green}{\text{直觉：样本均值约等于总体均值}}$

伯努利大数定律

$\color{green}{\text{直觉：样本概率约等于总体概率}}$

辛钦大数定律

条件：

独立
同分布
期望存在

故伯努利大数定律是辛钦伯努利大数定律的一个特例。

中心极限定理

中心极限定理均为：

$\text{若}x_i$ $\buildrel \rm iid(\text{独立同分布,identically distributed})\over{\backsim}$ $F,EX_i=\mu,DX_i=\sigma^2$

$\text{则} \displaystyle \sum_{i=1}^nx_i$ $\buildrel \rm x \to \infty \over{\backsim}$ $N(n\mu,n\sigma)(\text{正态分布})$

$\text{且} \dfrac{\displaystyle \sum_{i=1}^nx_i - n\mu}{\sqrt{n}\sigma}$ $\buildrel \rm x \to \infty \over{\backsim}$ $N(0,1)(\text{标准正太分布})$

中心极限定理说明样本的均值在总体均值的周围

ednow

基础30讲-概率论与数理统计-ch5-大数定律与中心极限定理