zy2022
概率论与数理统计
随机变量的数字特征
p500
引论:有的时候不需要知道概率分布,只需要知道数字指标
四个重要的知识,1个综合知识:
- E(x)数学期望
- D(x)方差
- Cov(x,y)协方差
- $\rho_{xy}$相关系数
- 不相关也能证明独立性
$\blacktriangleright$(为什么方差和期望啥的不需要小括号)
一维随机变量的数字特征
数学期望
是一个合理的平均值
概念
| 图片 | 要点 |
|---|---|
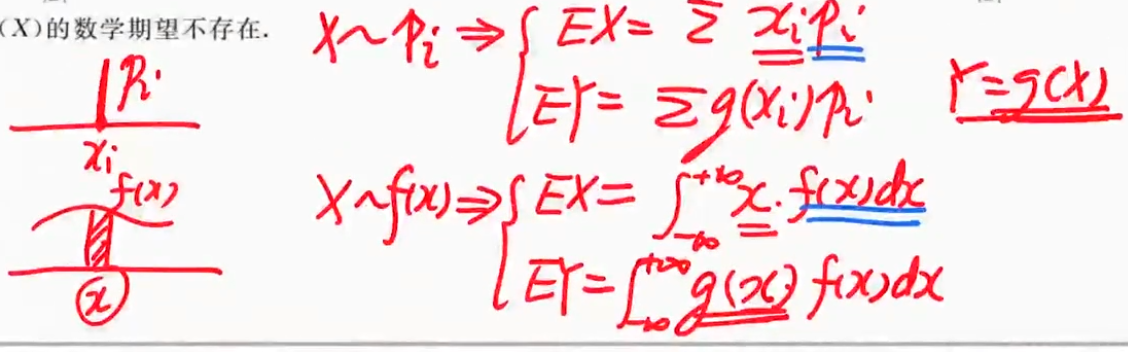 | 离散和连续的数学期望的定义 |
性质
| 图片 | 要点 |
|---|---|
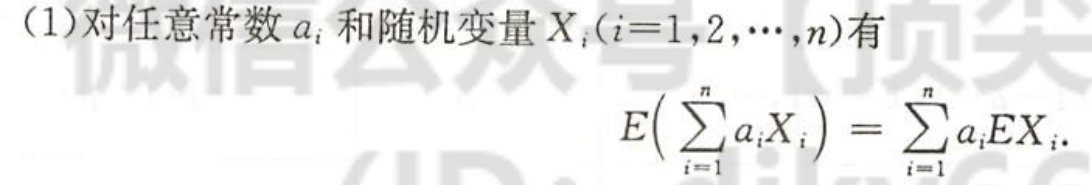 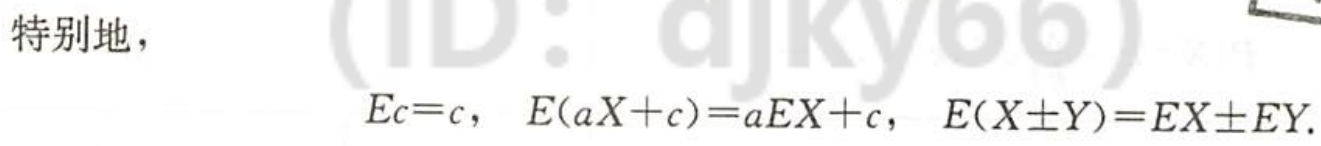 | 和差是无条件打开的 |
常数的期望是期望本身
独立的时候,乘积的方差才是方差的乘积
方差、标准差
引论:派运动员去参加运动会,选方差小的
概念
$DX=EX^2-(EX)^2$
性质
$EX^2 \geq (EX)^2$
| 图片 | 要点 |
|---|---|
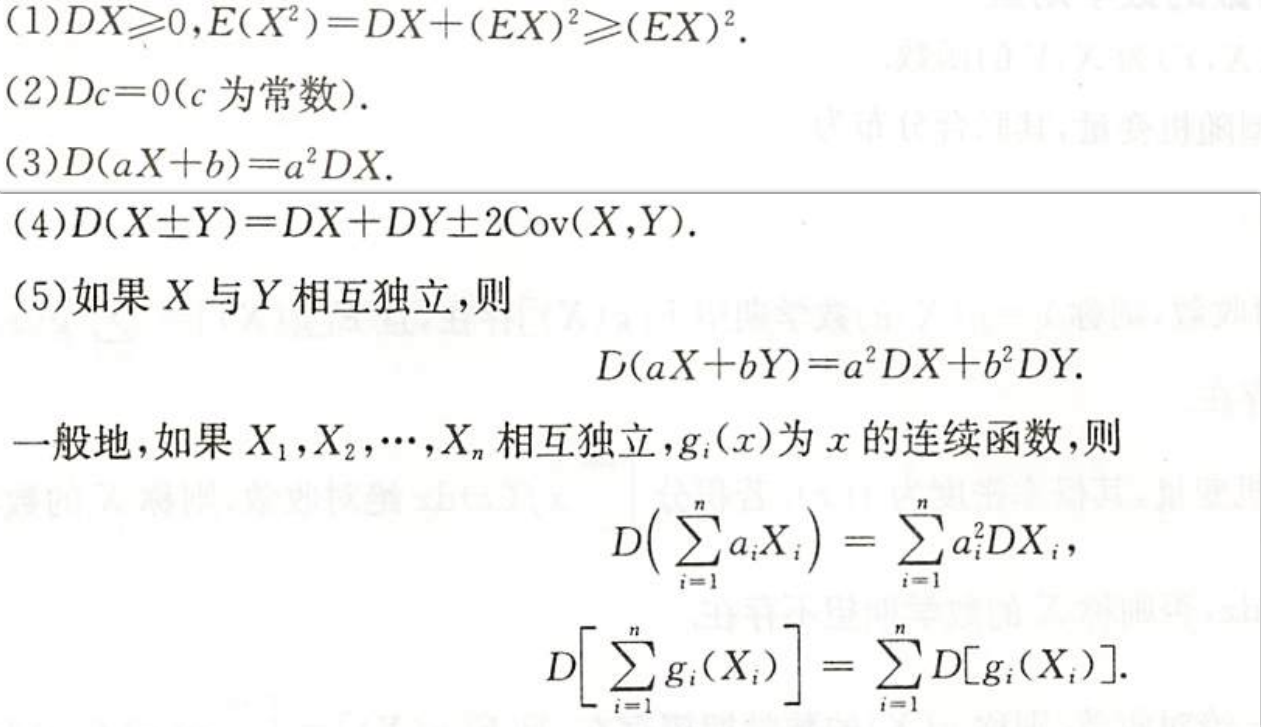 | 方差的性质 |
| 图片 | 要点 |
|---|---|
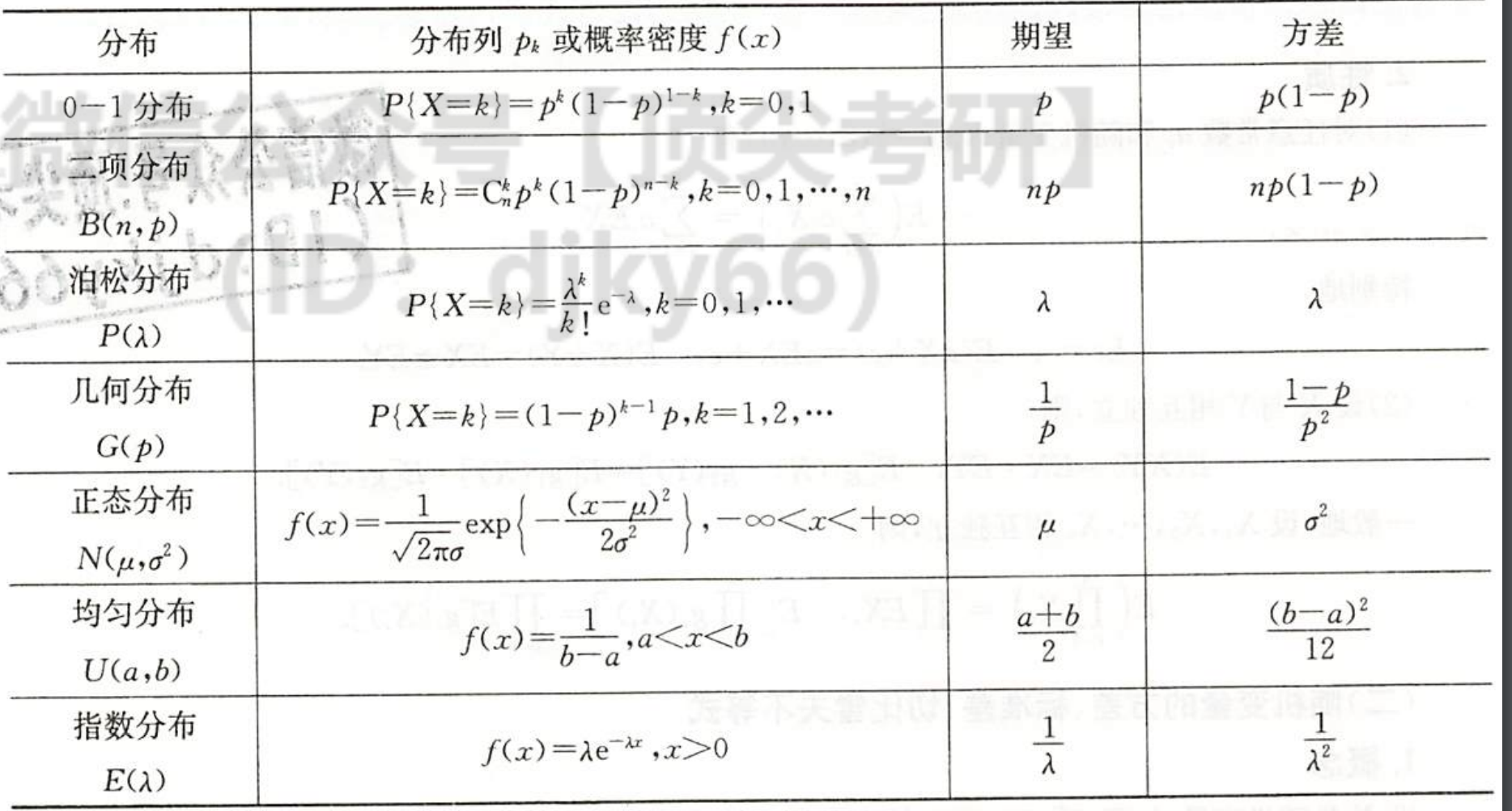 | 没有超几何分布 |
切比雪夫不等式
引论:描述了一次射击和这个运动员的平均水平的差距的关系,距离大于某个值的概率是不大的(第6讲也会用到)
二维随机变量的数字特征
数学期望
| 图片 | 要点 |
|---|---|
 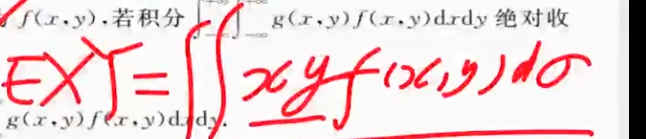 | 二维联合概率的数学期望计算 一般是协方差的一个步骤(红字部分) |
协方差与相关系数
概念
| 图片 | 要点 |
|---|---|
 | 协方差与相关系数的定义 |
| 图片 | 要点 |
|---|---|
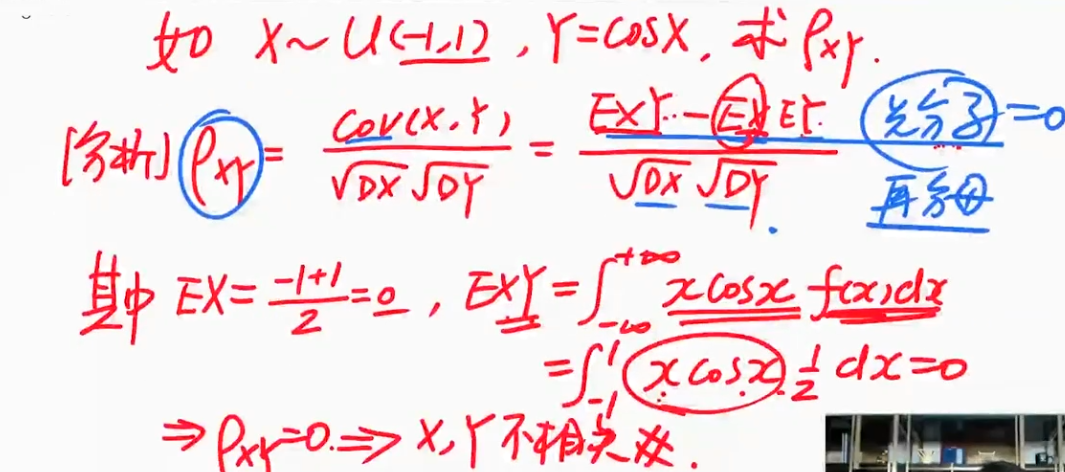 | 一道例题 先算分子,再算分母 用函数的奇偶性 |
相关性是描述线性相关性
性质
| 图片 | 要点 |
|---|---|
 | 协方差的综合 |
自己与自己的协方差是方差
独立性与相关性的判定
- 不相关也能证明独立性
- 独立:有纠缠关系
- 相关性:有线性相关关系
独立必定不相关
二维正态分布,X,Y独立$\iff$X,Y相关
相关必定不独立
| 图片 | 要点 |
|---|---|
 | 做题程序 |