zy2022
概率论与数理统计
多维随机变量及其分布
p472
三块知识点
- 定义
- 类型
- $\bigstar$ $\bigstar$ $\bigstar$函数的分布(大题考点)
四个新概念(相比于1维)
- 联合
- 边缘
- 条件
- 独立
$\text{条件}= \dfrac{\text{联合}}{\text{边缘}}$
独立性就是检验$\text{联合}=\text{边缘的乘积}$
二维(n维)随机变量
| 图片 | 要点 |
|---|---|
  | 总结, 独立性:对于每一个ij都是边缘概率的乘积 |
分布函数 $f(x,y)$ 与概率P{Y $\leq$ X}

概念
联合分布函数
| 图片 | 要点 |
|---|---|
 | 联合分布函数 |
概念
性质
边缘分布函数
| 图片 | 要点 |
|---|---|
 | 边缘分布函数 |
联合分布律
图片详情

边缘分布律
图片详情
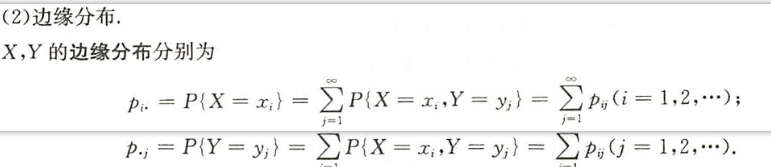
条件分布律
二维连续型随机变量
| 图片 | 要点 |
|---|---|
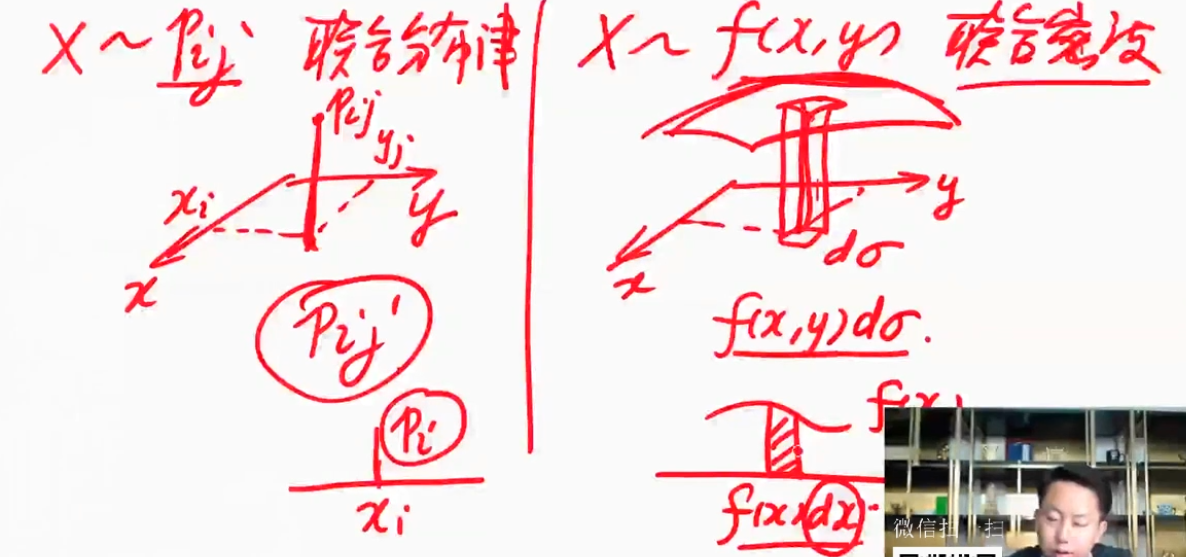 | 联系二维离散型随机变量和二维连续型随机变量 |
联合概率密度
图片详情

边缘概率密度
| 图片 | 要点 |
|---|---|
 | 求谁不积谁 不积先定限 限内画条线 先交写下限 后交写上限 |
条件概率密度
条件密度和条件分布函数

即 $\text{条件}=\dfrac{\text{联合}}{\text{边缘}}$
联合分布函数与概率密度、边缘概率密度、条件概率密度
联合分布函数与概率密度、边缘概率密度、条件概率密度

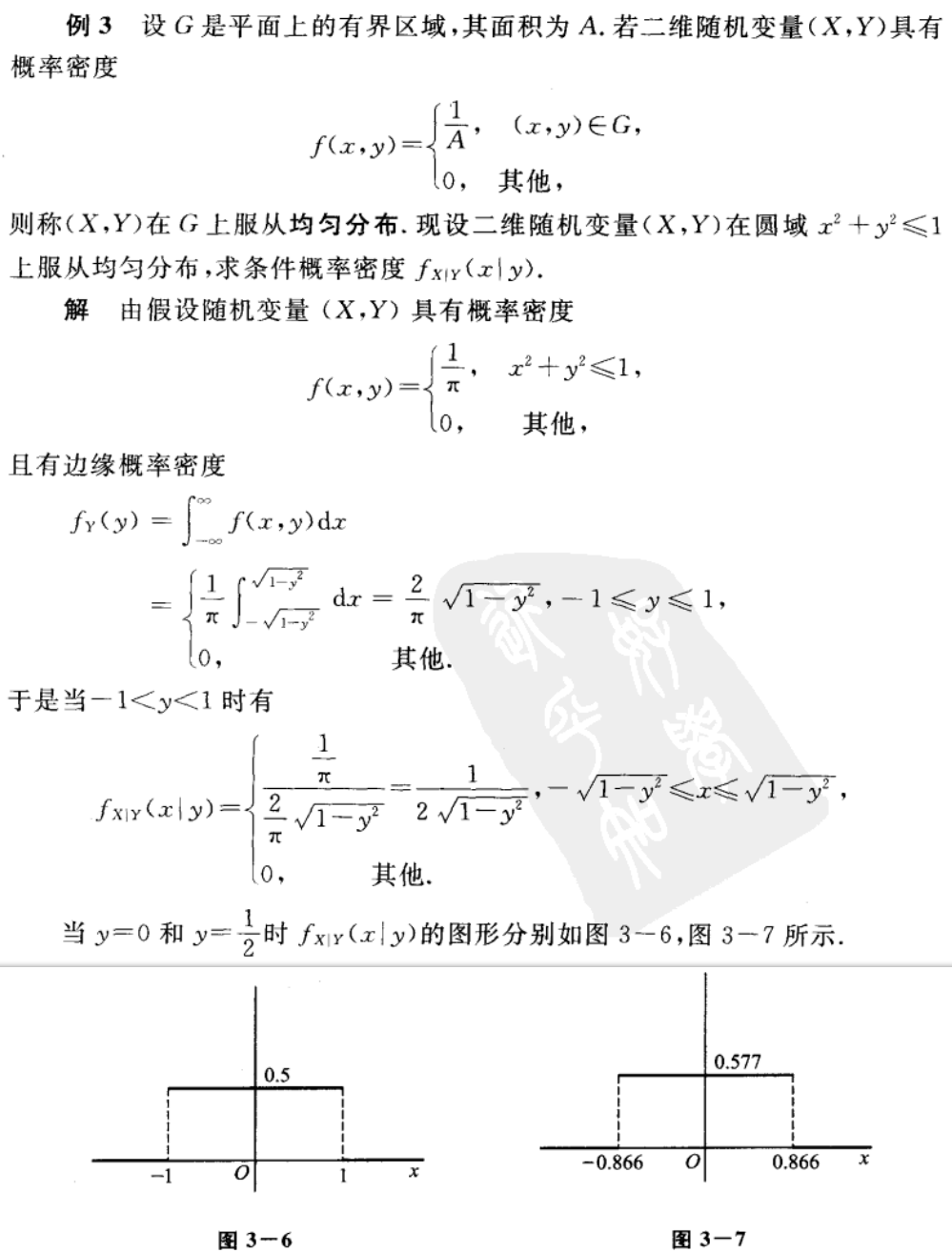
二维均匀分布
二位均匀分布就是几何概型
二维均匀分布与定义、例题
二维正态分布
图片详情

要考就考数字特征
独立性
- 两个以上变量就会关注独立性
| 图片 | 要点 |
|---|---|
 | 注意对比原来的公式,实际做题还要交$G_{\text{正}}$ |
概念
相互独立的充要条件
$F(x,y)=F_X(x)\cdot F_Y(y)$
$P_{ij}=P_i\cdot P_j$
$fx,y)=f_X(x)f_Y(y)$
性质
图片详情

独立的性质

函数的分布
| 图片 | 要点 |
|---|---|
 | U实际上是一维的 |
(离散型,离散型)→离散型
(连续型,连续型)→连续型
分布函数法
卷积公式
记忆方法:
- 积谁不换谁
- 换完求偏导
| 图片 | 要点 |
|---|---|
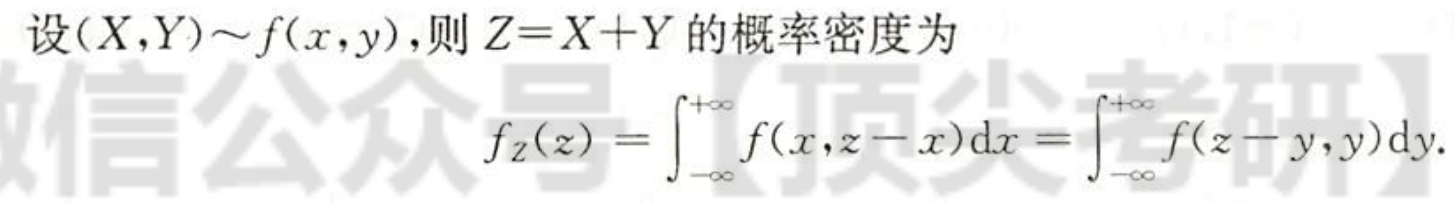   | 和的分布, 注:证明的蓝色部分是要求掌握的,涉及高等数学的知识 |
| 图片 | 要点 |
|---|---|
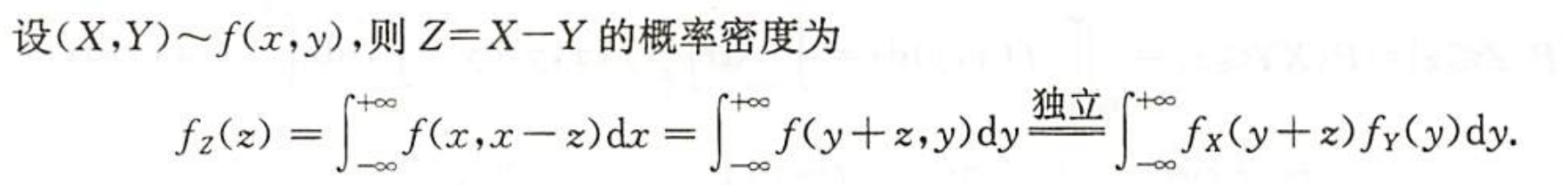 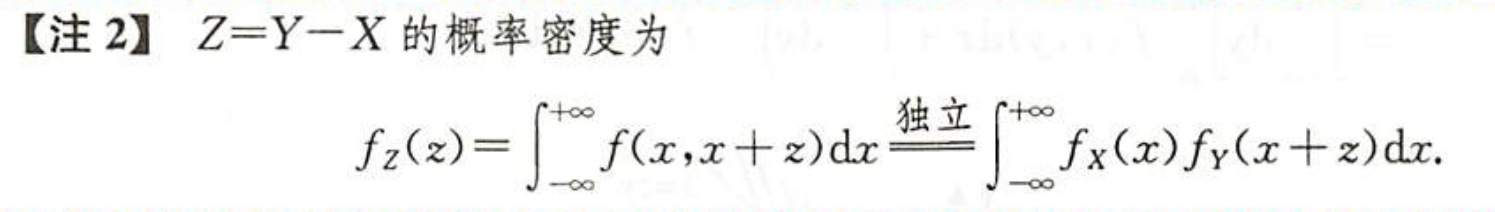 | 差的分布 |
| 图片 | 要点 |
|---|---|
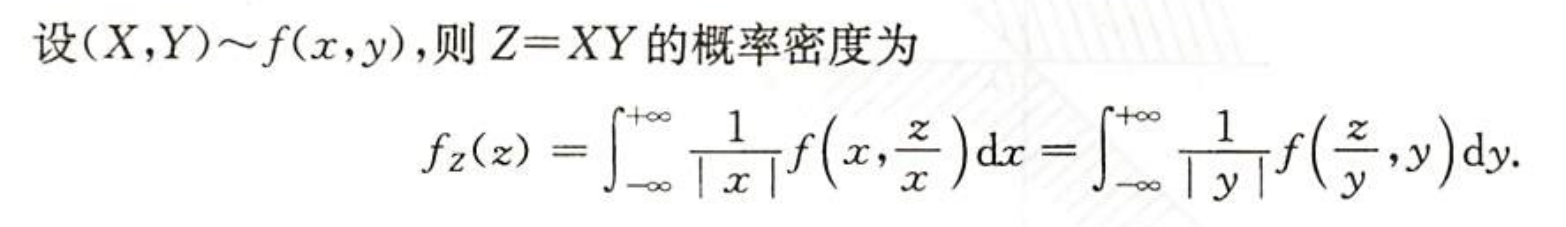 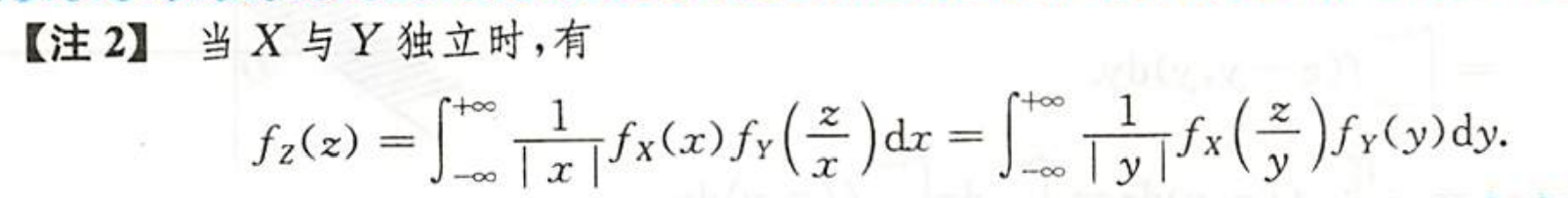 | 积的分布 |
| 图片 | 要点 |
|---|---|
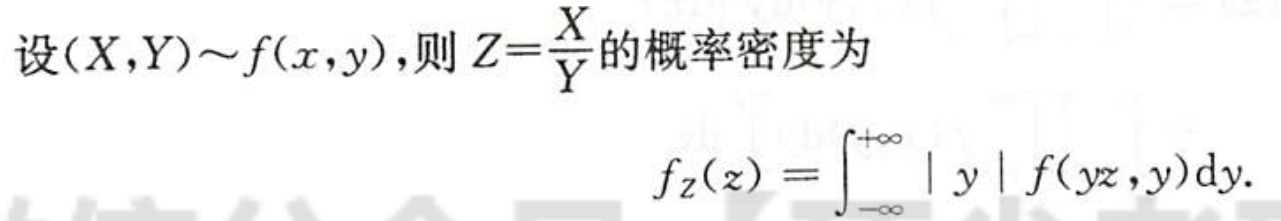 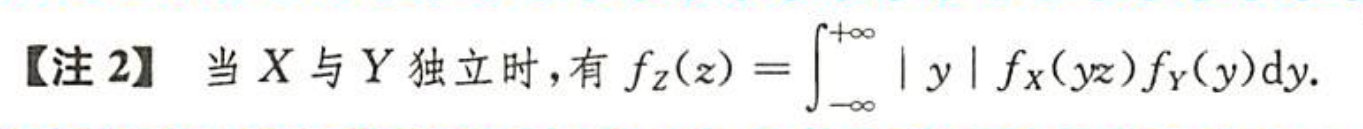 | 商的分布, 只记y的比较好求 |
max的分布
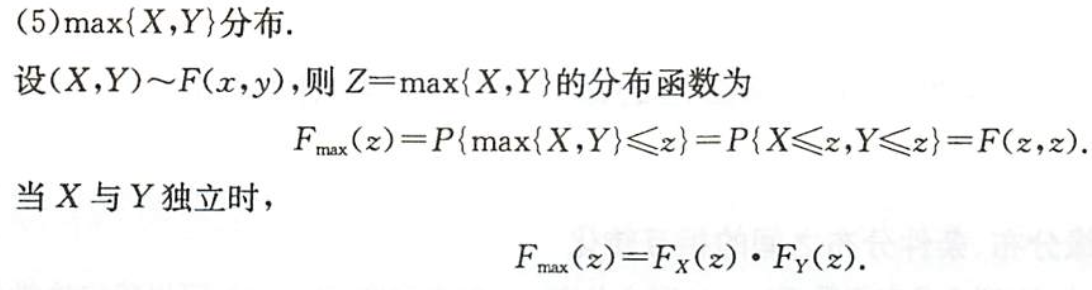
min的分布

n个相互独立的随机变量

分布的可加性

(离散型,连续型)→连续型
(离散型,连续型)→连续型使用全概率公式
图片详情

