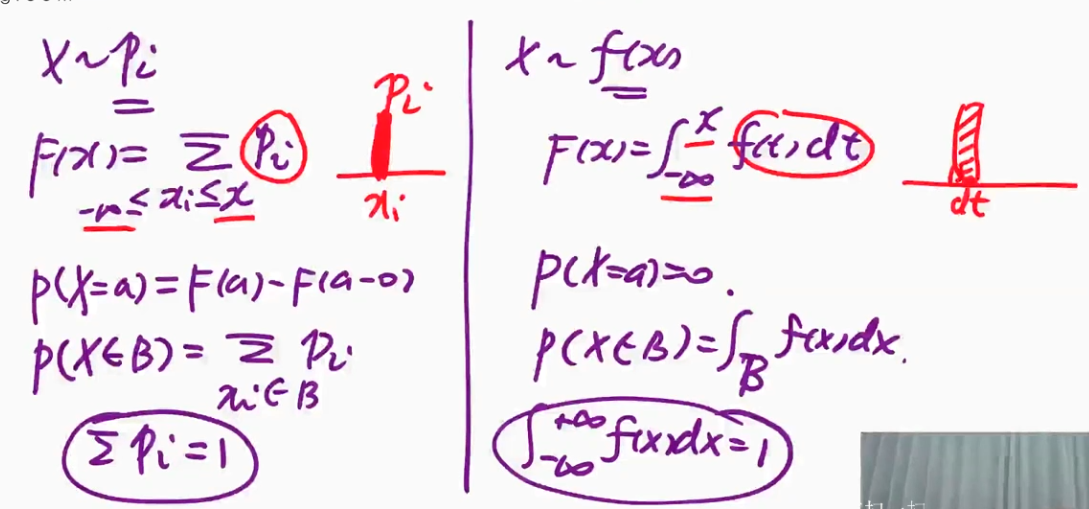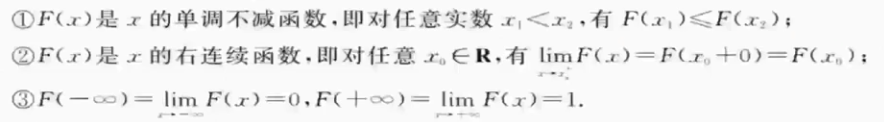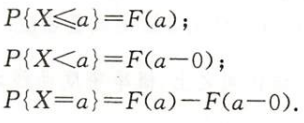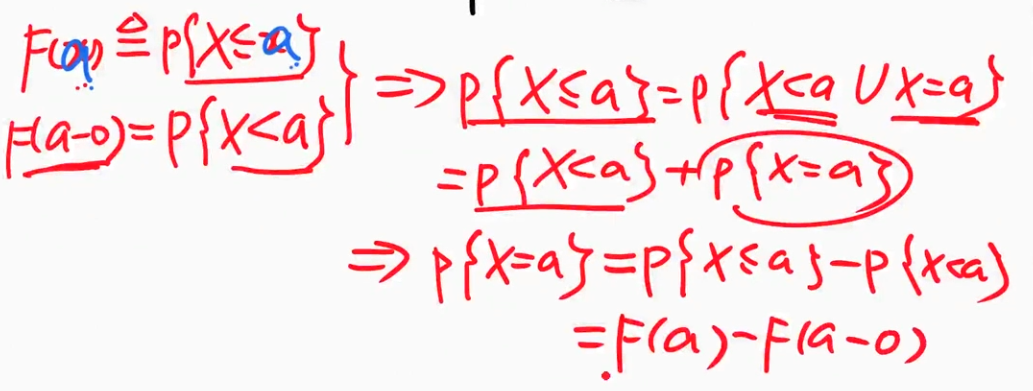zy2022
概率论与数理统计
一维随机变量及其分布
p448
$\sharp$ 学科有研究对象和研究工具
- 数学上,研究对象(统一化,数字化)
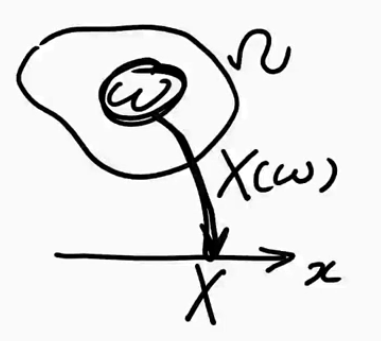
- (如上图)随机变量: 定义在样本空间上,取值在实数轴上的函数交随机变量$(r,v)\qquad X=X(\Omega)$
离散和连续随机变量的对比
八大分布是结构性知识
$f(x)\text{(密度)可以唯一确定}F(x)\text{(分布函数)}$,反之不然
- f(x)改变有限个值不改变,F(x)的值,在定积分里面学的
一维随机变量
概念
分布函数
分布函数的定义域一定是整个实数轴,x取遍$-\infty$导$+\infty$
研究范围从$\emptyset$(空集)一直到$\Omega$(全集)
概念
性质
- 单调不减
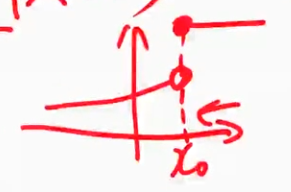
- 右连续(左空心右实心)(体现在题目上:等号跟着大于号,即例如$0 \leq x< 1$)
- 极限状态
- 有界性
应用——求概率
- 证明
a-0相当于左极限值
一维离散型随机变量
如果随机变量X只可能取有限个或可列个值,则称X为离散型随机变量
$X \backsim p_i$念作X服从$p_i$
需要掌握的知识点:
- 定义
- 所有概率加起来为1(归一性)
- 求一点函数的概率
- 求区间函数的概率
分布律
分布列,分布律,概率分布
性质
应用—求概率
五大分布
0-1分布$B(1,p)$
$$
\text{伯努利计数变量} X \backsim \begin{pmatrix}
1 & 0 \cr
p & 1-p
\end{pmatrix}
$$
即 $P\lbrace X=1 \rbrace=p,P\lbrace X=0 \rbrace =1-p$,称 $X$ 服从参数 $p$的0-1分布,记为 $X \backsim B(1,p)$
| 图片 | 要点 |
|---|---|
 | 独立实验 独立重复试验 伯努利试验 例子:投篮 |
二项分布$B(n,p)$
$P\lbrace X \rbrace = C_n^kp^k(1-p)^{n-k}$,称$B(n,p)$
泊松分布$P(\lambda)$
$$
P\lbrace X=k \rbrace = \dfrac{\lambda^k}{k!}e^{-\lambda}
$$
念作$X$服从参数为$\lambda$的泊松分布
$\lambda$是强度
作用:某场合某单位时间内源源不断的质点来流的个数。
- 例子:超市 8.00-9.00 源源不断的 客户来的个数
- 例子:节假日的人流
注意:也可用来研究稀有事件发生的概率
几何分布$G(p)$
首中即停
$$
p \lbrace X \rbrace =p(1-p)^{k-1}
$$
意义:
- 首次出现故障就停止,广泛应用在寿命分布中
- 守株待兔
超几何分布$H(n,N,M)$
古典概型的一种特殊情况
| 图片 | 要点 |
|---|---|
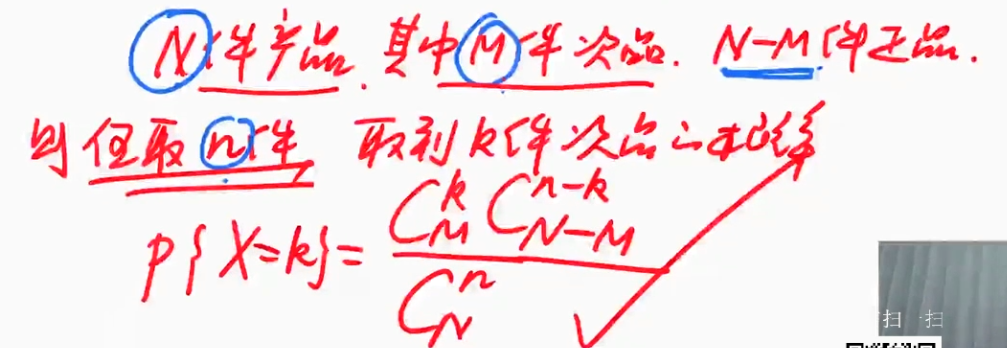 | 一个例子解释超几何分布 |
一维连续型随机变量
$X \backsim F(x)$ $\buildrel \rm \Delta \over{=}$ $p \lbrace X \leq x\rbrace=\int_{-\infty}^xf(t)dt$
- 被积函数是可积函数,其被积函数必然连续
需要掌握的知识点:
- 定义
- 所有概率加起来为1(归一性)
- 求一点函数的概率
- 求区间函数的概率
概率密度
性质
应用-求概率
三大分布
均匀分布
相当于几何概型的一维情形
| 图片 | 要点 |
|---|---|
 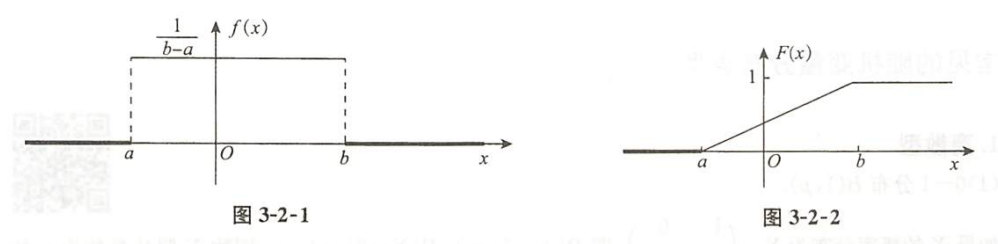 | 均匀分布的定义 |
高级说法:$X\text{在}I$上的任一子区间取值的概率与该子区间长度成正比$\implies$ $X \backsim U(I)$
指数分布
| 图片 | 要点 |
|---|---|
 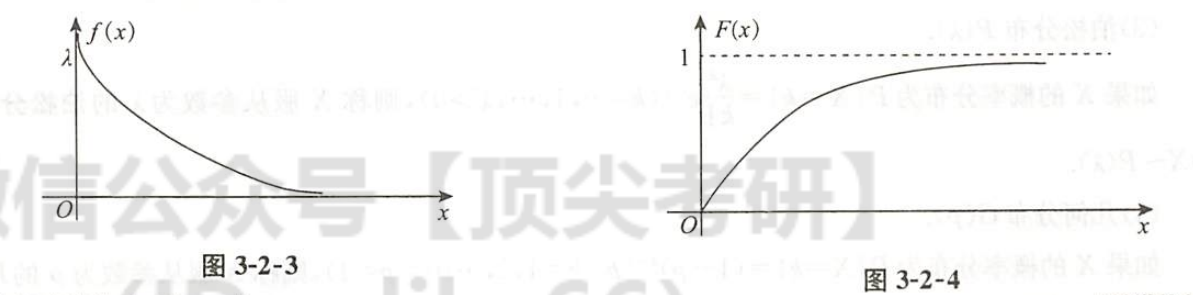 | 指数分布的定义 |
等待型分布(几何分布也是)
- 几何分布:离散
- 指数分布:联系
$\lambda$是机器坏的失效率,兔子来撞树
正态分布
| 图片 | 要点 |
|---|---|
 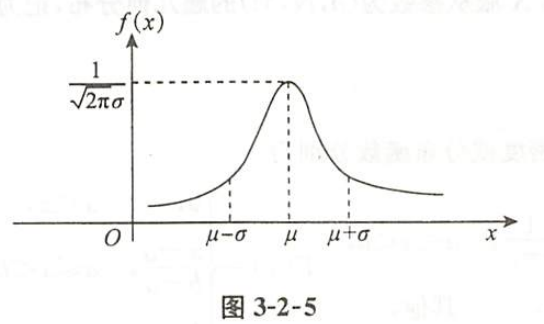 | 正态分布概率密度 |
| 图片 | 要点 |
|---|---|
 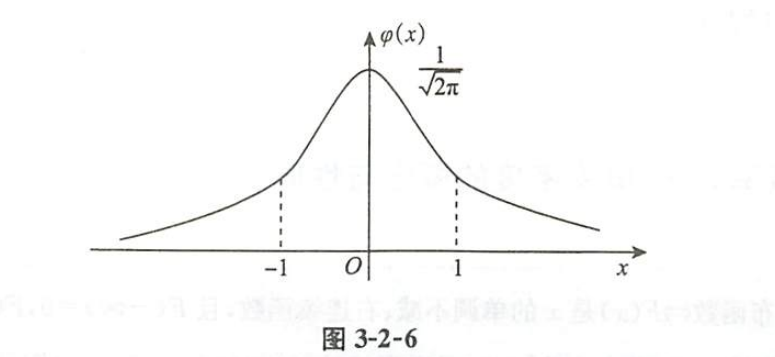 | 标准正态分布 |
| 图片 | 要点 |
|---|---|
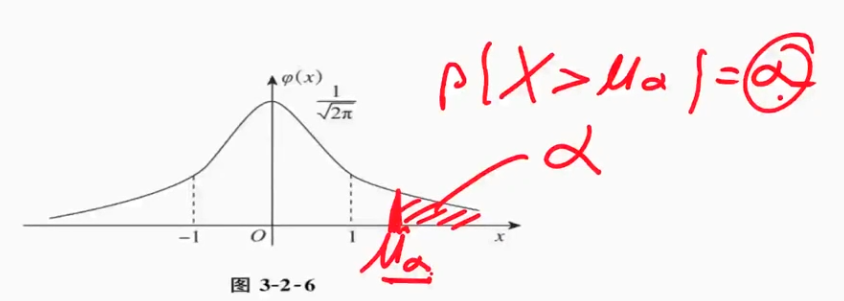 | 上$\alpha$分位点($\mu_\alpha$),右侧围出$\alpha$时,对应的点$\mu_\alpha$是多少 |
| 图片 | 要点 |
|---|---|
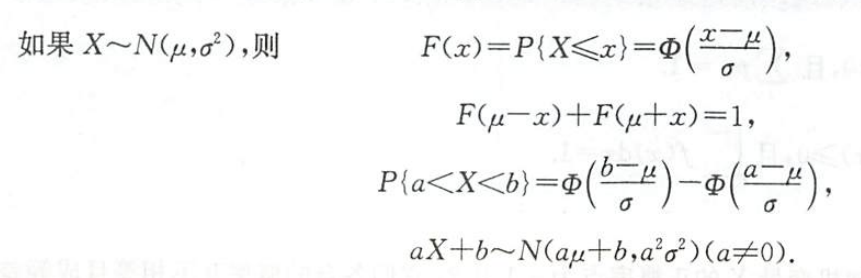 | 1.把正态分布标准化 2.用上$\alpha$的推导画图研究 3.正态分布的范围转化为标准正态分布的范围 正态分布的数字特征 |
一维随机变量函数的分布
| 图片 | 要点 |
|---|---|
 | 引论,射击游戏的积分制度 |
离散型→离散型
连续型→连续型(混合型)
解题步骤