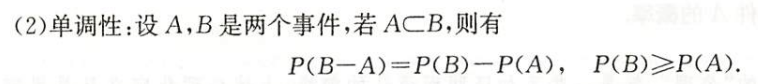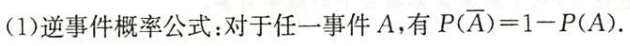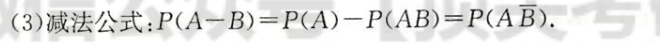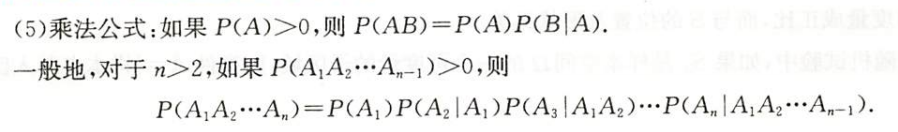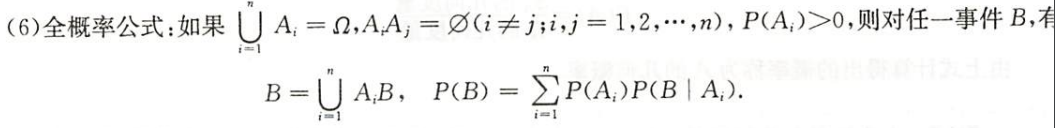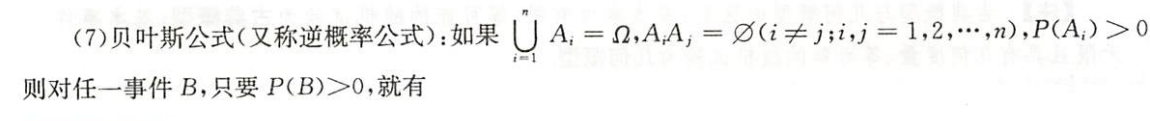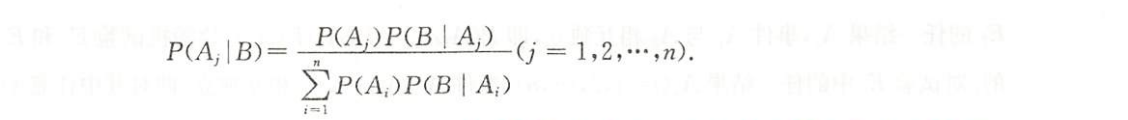zy2022

概率论与数理统计

随机事件与概率

p427

一般是5分小题

重要的三个考点

古典概型求概率
几何概型求概率
重要公式求概率

只考5个题?

基本概念

随机试验

$E$表示

(1)试验可以在相同的条件下重复进行;

(2)试验所有可能结果是明确可知道的,并且不止一个;

(3)每一次试验会出现哪一个结果,事先并不能确定.

随机事件

在一次试验中可能出现,也可能不出现的结果称为随机事件,简称事件,并用大写字母A,B,C等表示.为讨论需要,将每次试验中一定发生的事件称为必然事件,记为$\Omega$.每次试验中一定不发生的事件称不可能事件,记为$\emptyset$.

样本空间

随机试验的每一个可能结果(不可再分)称为样本点,记为$\omega$.样本点的全体组成的集合称为样本空间(或基本事件空间),记为$\Omega$,即$\Omega={\omega}$.由一个样本点构成的事件称为基本事件.随机事件A总是由若干个基本事件组成,即A是$\Omega$的子集.

事件的关系与运算

关系

包含

(1)如果事件A发生必导致事件B发生,则称事件B包含事件A(或A被B包含),记为A$\subset$B.

相等

(2)如果A$\subset$B且B$\subset$A,则称事件A与B相等,记为A=B.A与B相等,事实上也就是说,A与B由完全相同的一些试验结果构成,它不过是同一事件表面上看来两个不同的说法而已.

相容

(3)称“事件A与B同时发生”的事件为事件A与B的积(或交),记为A$\cap$B或AB.

(4)若AB$\neq \emptyset$,则称事件A和B相容;若AB=$\emptyset$,则称事件A与B互不相容,也叫互斥.如果一些事件中任意两个事件都互斥,则称这些事件是两两互斥的,或简称互斥的.

(5)称“事件A与B至少有一个发生”的事件为事件A与B的和(或并),记为A$\cup$B.

对立

(6)称“事件A发生而事件B不发生”的事件为事件A与B的差,记为A-B;称“事件A不发生”的事件为事件A的逆事件或对立事件,记为$\bar{A}$

由定义易知$A-B=A-AB=A\bar{B},\qquad B=\bar{A} \iff AB= \emptyset \text{且}A \cap B= \Omega$

(7)称有限个(或可列个)事件$A1,A_2,\cdots,A_n,(\cdots)$构成一个完备事件组,如果$\displaystyle \bigcap{i=1}^nA_i=\Omega,\quad A_iA_j = \emptyset(\text{对一切}i\neq j;i,j=1,2,\cdots,n(\cdots))$.

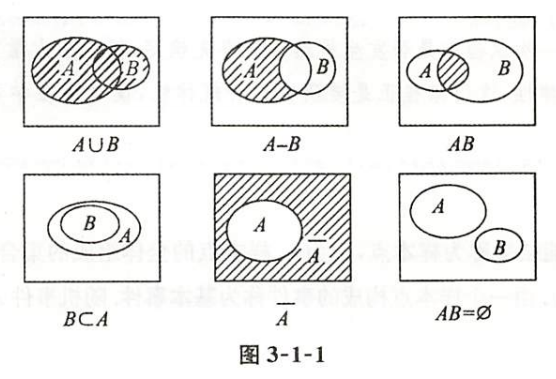
(8)事件的关系与运算可以用文氏图形象地表示出来(如图3-1-1),图中的矩形表示必然事件$\Omega$.

运算

和(并)

差

积(交)

运算法则

吸收律

交换律

结合律

分配律

$\bigstar$ 对偶律(德·摩根律)

概率的定义

描述性定义

通常将随机事件A发生的可能性大小的度量(非负值),称为事件A发生的概率,记为P(A).

统计性定义

在相同条件下做重复试验,事件A出现的次数k和总的试验次数n之比$\dfrac{k}{n}$,称为事件A在这n次试验中出现的频率.当试验次数n充分大时,频率将“稳定”于某常数的“附近”.n越大,频率偏离这个常数的可能性越小.这个常数p就称为事件A的概率.

公理化定义

每个事件的事件函数满足
(1)非负性

(2)规范性

(3)可列可加性

古典概型和几何概型

(1)称随机试验(随机现象)的概率模型为古典概型,如果其样本空间(基本事件空间)满足:

${\textstyle\unicode{x2460}}$ 只有有限个样本点(基本事件);

${\textstyle\unicode{x2461}}$ 每个样本点(基本事件)发生的可能性都一样.(等可能)

如果古典概型的基本事件总数为n,事件A包含k个基本事件,也叫作有利于A的基本事件为k 个，则A的概率为

$P(A) = \dfrac{k}{n}=\dfrac{\text{事件}A\text{所含基本事件的个数}}{基本事件总数}$

古典概型

不要研究的太过痴迷

数数法

(1) 枚举法

(2) 集合对应法

加法原理（n种方法，每种方法有m个）
乘法原理(n步骤，每个不走有m个方法)
排列
组合
逆数法(求对立事件数)

最主要的两个知识点：随机分配，简单随机抽样

随机分配

简单随机抽样

几何概型

${\textstyle\unicode{x2460}}$ 样本空间(基本事件空间)$\Omega$是一个可度量的有界区域;

${\textstyle\unicode{x2461}}$ 每个样本点(基本事件)发生的可能性都一样,即样本点落入$\Omega$的某一可度量的子区域S的可能性大小与S的几何度量成正比,而与S的位置及形状无关.

$P(A) = \dfrac{S_A\text{的几何度量}}{\Omega\text{的几何度量}}$

概率的基本性质与公式

性质

有界性

(1)有界性:对于任一事件A,有0≤P(A)≤1,且 P($\emptyset$)=0(不可能事件的概率是0),P($\Omega$)=1(必然事件的概率是1).

$P(A)=0 \nRightarrow A=\emptyset, \qquad A=\emptyset \implies P(A)=0$

例子，8.00-9.00内到达，8.30到达在几何概型里面概率是0，概率为0不一定不能发生

$P(A)=1 \nRightarrow A=\Omega, \qquad A=\Omega \implies P(A)=1$

例子，除了8.30不到，$\Omega$不是1

单调性

公式

逆事件概率公式

加法公式

减法公式

减法公式的推导

条件概率公式

乘法公式

全概率公式

全集分解公式

由因导果

贝叶斯公式(又称逆概率公式)

执果索因

信息增加后，有些事情的概率会变化

独立性

事件的独立性

(1)描述性定义(直观性定义)设A,B为两个事件,如果其中任何一个事件发生的概率不受另外一个事件发生与否的影响,则称事件A与B相互独立.

(2)数学定义设A,B为两个事件,如果P(AB)=P(A)P(B),则称事件A与B相互独立,简称为A与B独立.

事件的独立性的性质
$A\text{、}B\text{独立} \iff \bar{A} \text{、} \bar{B} \text{独立} \iff A \text{、} \bar{B} \text{独立} \iff \bar{A} \text{、} B \text{独立}$

n=3的情况