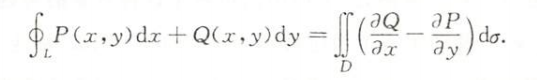zy2022
高等数学
三重积分与曲线曲面积分
- 集高等数学与一身
三重积分
三重积分的概念、性质与对称性
概念
- 可以用密度与质量去理解
性质
性质1(求空间区域的体积)
性质2(可积函数必有界)
性质3(积分的线性性质)
性质4(积分的可加性)
性质5(积分的保号性)
性质6(三重积分的估值定理)
性质7(三重积分的中值定理)
$\bigstar$ 对称性
普通对称性
图片详情

轮换对称性
图片详情
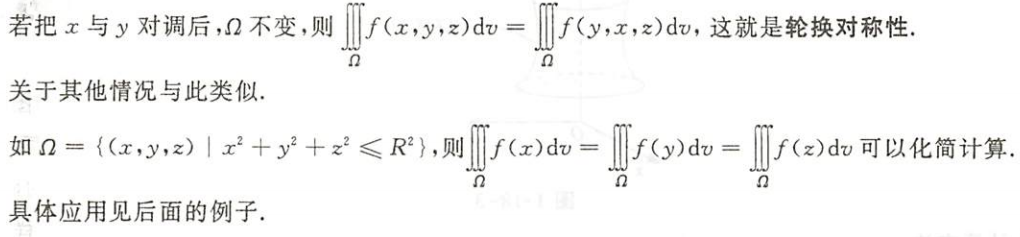
三重积分的计算
基础方法
直角坐标系
先一后二
别称(先$z$后$xy$法,也叫投影穿线法)
适用场合:$\Omega$有下曲面$z=z_1(x,y)$、上曲面$z=z_2(x,y)$.无侧面或侧面为柱面
计算方法:
$$\iiint_\Omega f(x,y,z)dv=\iint_{D_{xy}}d\sigma \int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dz$$
步骤口诀
- 后积先定限
- 限内画条线
- 先交写下限
- 后交写上限
先二后一
别称(先$xy$后$z$法,也叫定限截面法)
适用场合:$\Omega$是旋转体,其旋转曲面方程为$\Sigma:z=z(x,y)$
计算方法:
$$\iiint_\Omega f(x,y,z)dv=\int_a^bdz \iint_{D_z}f(x,y,z)d\sigma$$
步骤口诀
- 后积先定限
- 限内截个面
柱面坐标系
- 定积分+极坐标系下的二重积分(先二后一法)
在直角坐标系的先一后二法中,若$\iint_{D_{xy}}适用于极坐标系,$
$$
\text{则}\begin{cases}
x = rcos\theta , & \cr
y = rsin\theta , & \cr
\end{cases}
\text{便有}
$$
$$
\iiint_\Omega f(x,y,z)dxdydz = \iiint_\Omega f(rcos \theta,r sin\theta,z)rdrd\theta dz
$$
球面坐标系
适用场合
- 被积函数中含$f(x^2+y^2+z^2)\text{、}f(x^2,y^2)$
计算方法
$$
\text{令}\begin{cases}
x=rsin(\varphi)cos\theta, & \cr
y=rsin(\varphi)sin\theta, & \cr
z=rcos(\varphi), &
\end{cases}
$$
计算公式
$$
\iiint_\Omega f(x,y,z)dxdydz = \iiint_\Omega f(rsin(\varphi)cos\theta,rsin(\varphi)sin\theta,rcos(\varphi))r^2sin(\varphi)d\theta d \varphi dr
$$
技术方法
对称性
形心公式的逆用
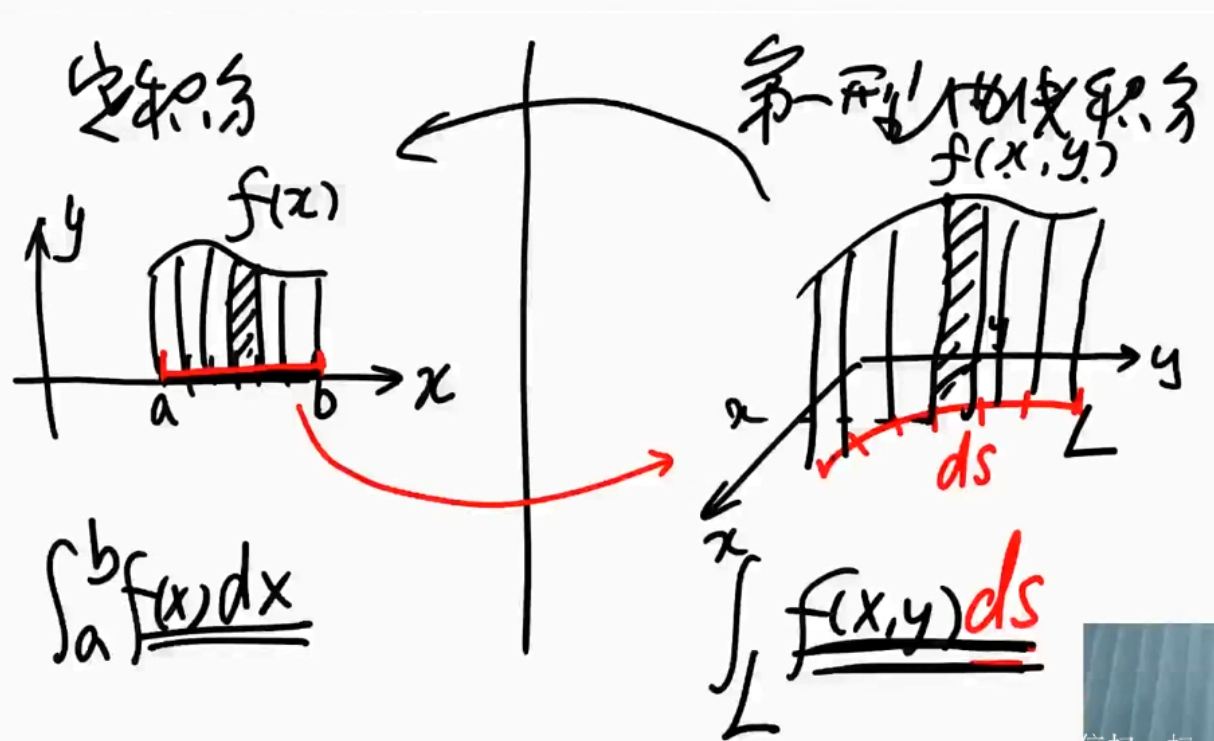
第一型曲线积分
概念、性质与对称性
概念
- 定积分定义在“直线段”上,第一型曲线积分定义在“曲线段”上
性质
性质 8 (求空间曲线的长度)
性质9 (可积函数必有界)
性质10 (积分的线性性质)
性质11 (积分的可加性)
性质12(积分的保号性)
性质13(第一型曲线积分的估值定理)
性质14(第一型曲线积分的中值定理)
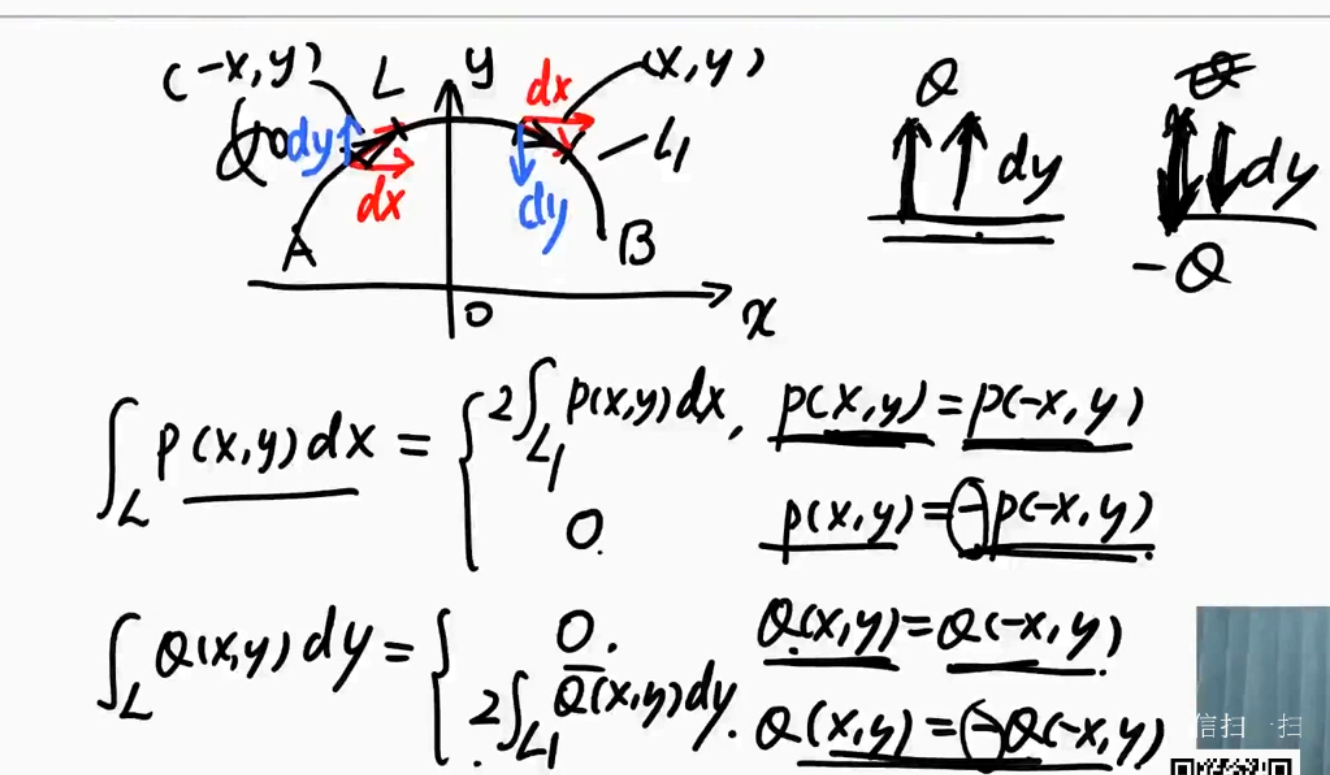
对称性
普通对称性
图片详情

轮换对称性
图片详情
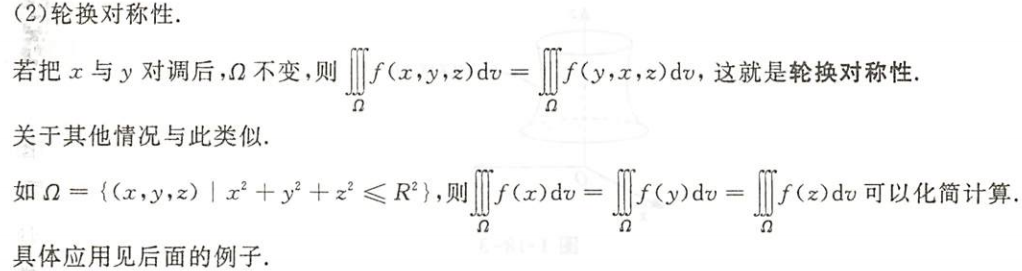
计算
基础方法-化为定积分
空间形式
${\textstyle\unicode{x2460}}$ 参数式
空间形式的计算公式
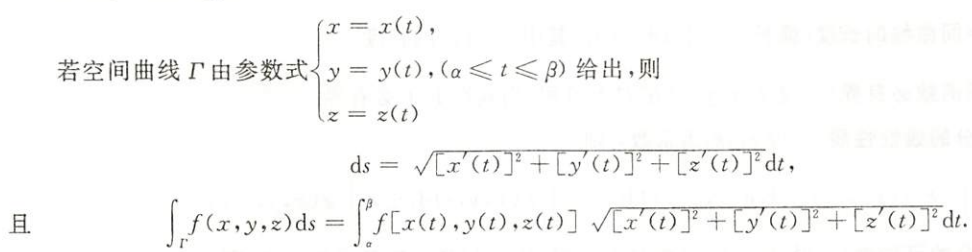
平面情形
${\textstyle\unicode{x2460}}$ 显式
${\textstyle\unicode{x2460}}$ 参数式
${\textstyle\unicode{x2460}}$ 极坐标形式
平面情形的计算方法
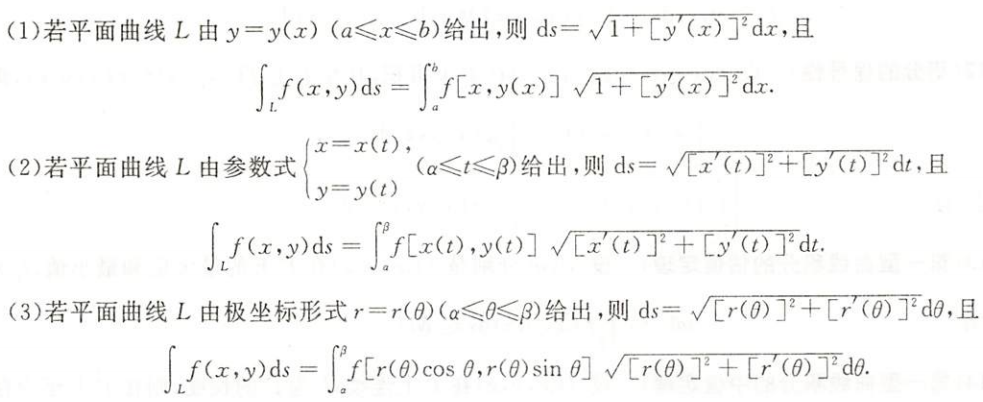
技术方法
边界方程代入被积函数
对称性
形心公式的逆用
图片详情
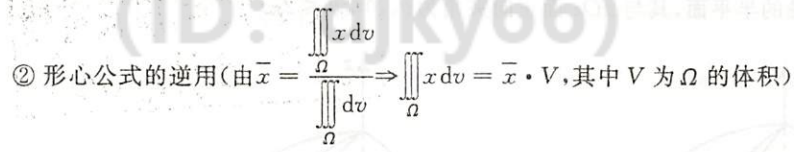
第一型曲面积分
跟二重积分对比
概念性质与对称性
概念
性质
对称性
普通对称性
轮换对称性
计算
基础方法-化为二重积分
基础方法-化为二重积分

技术方法
边界方程代入被积函数
对称性
形心公式的逆用
应用
重积分与第一型线面积分的应用
一个体系:二重、三重、一线、一面
几何量
平面区域
图片详情

面积
空间区域
体积
图片详情

空间曲线
弧长
图片详情
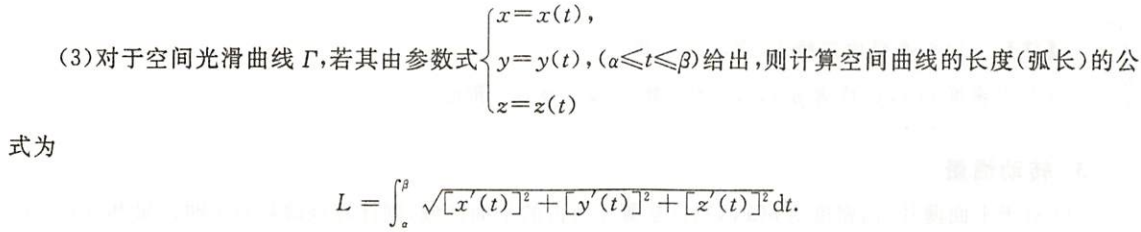
空间曲面
面积
图片详情

重心(质心)与形心
- 密度是常数的时候,重心就是形心
形心公式的逆用
平面薄片
图片详情

空间物体
- $\bigstar$ 喜欢用三重积分考重心
图片详情

空间曲线
图片详情
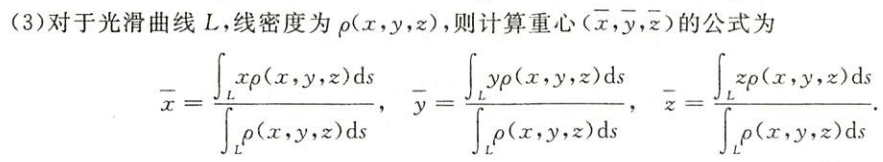
空间曲面
图片详情

转动惯量
- 从未考过,未来会考
平面薄片
图片详情
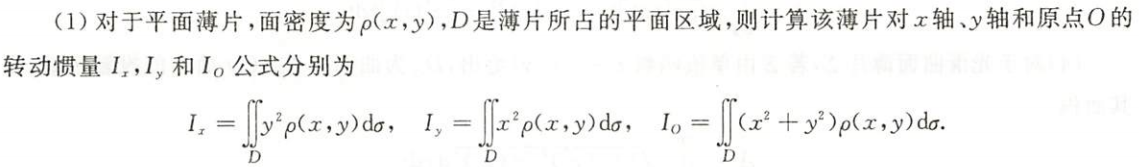
空间物体
图片详情

空间曲线
图片详情

空间曲面
图片详情

引力
平面薄片
图片详情

空间物体
图片详情

空间曲线
图片详情

空间曲面
图片详情

第二型曲线积分
- 既有长度也有方向
- 变力沿着曲线做功
对称性问题
第二型曲线积分的概念与性质
场的概念
图片详情

变力沿曲线做功
图片详情

第二型曲线积分的概念
图片详情

第二型曲线积分的性质
图片详情

平面第二型曲线积分的计算
基础方法-化为定积分
图片详情

格林公式法
- $\bigstar$ $\bigstar$ $\bigstar$
- 公式的使用一定保证D是封闭区域(L是封闭曲线)
- 左手在D内,为L的正向,记为$L^+$(反向要添负号)
- $P\text{、}Q$有一阶连续偏导数
- 形心公式的逆用
第二型曲面积分
- 研究通量的概念
- 流出为正,流入为负
- 跟投影的轴锐角为正,钝角为负
- 海域找源头
外法向(题目告知)
第二型曲面积分的概念与性质
向量场的通量
图片详情

第二型曲面积分的概念
图片详情

$$
\iint_{\Sigma}P(x,y,z)dydz + Q(x,y,z)dzdx + R(x,y,z)dxdy
$$
第二型曲面积分的性质
图片详情
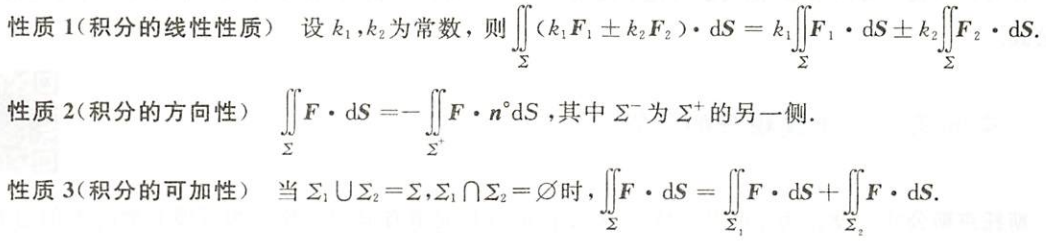
性质1(积分的线性性质)
性质2(积分的方向性)
性质3(积分的可加性)
第二型曲面积分的计算
基本方法-化为二重积分
拆成三个积分,分别投影到相应的坐标面上,化为二重积分计算,然后再相加,以$R(x,y,z)dxdy$为例子
(1) 将$\Sigma$投影到某一平面(比如$xOy$面)上$\implies$投影区域为$D$(比如$D_{xy}$)
(2) 将$z=z(x,y)$或者$F(x,y,z)=0$代入$R(x,y,z)$
(3) 将$dxdy$写成“$\pm dxdy$”,其中$\Sigma$方向向上(即法向量与z轴夹角为锐角)时取“+”,否则取“—”.
这就把第二型曲面积分化为了二重积分,得到
$$
\iint_{\Sigma}R(x,y,z)dxdy=\pm \iint_{D_{xy}}R(x,y,z(x,y))dxdy
$$
同样需要指出的是,投影时$\Sigma$上的任何两点的投影点不能重合
图片详情

高斯公式法
- ${\textstyle\unicode{x2460}} \Sigma$封闭曲面(封闭的区域$\Omega$)
- ${\textstyle\unicode{x2461}} \Omega$取外侧
- ${\textstyle\unicode{x2462}} P,Q,R$具有一阶连续偏导数
$$
\unicode{x222F}_\Sigma Pdydz + Qdzdx + Rdxdy = \iiint_\Omega (\dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z})dv
$$
需要掌握“补面法”和“挖去法”
例题1

例题2

空间第二型曲线积分的计算
斯托克斯公式
- 选平面最简单
$$
\unicode{x222E}_l Pdx+Qdy+Rdz = \iint_\Sigma \begin{vmatrix}
cos\alpha & cos \beta & cos \gamma \cr
\dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial }{\partial z} \cr
P & Q & R
\end{vmatrix} dS
$$