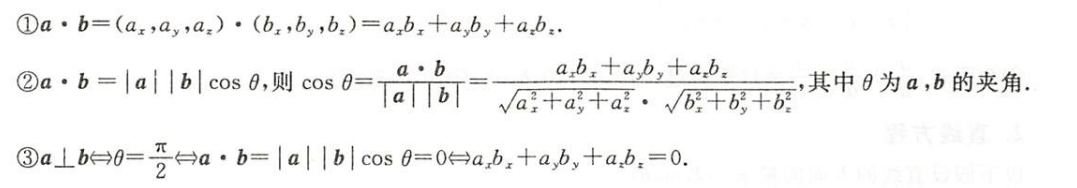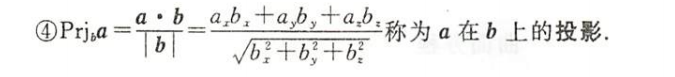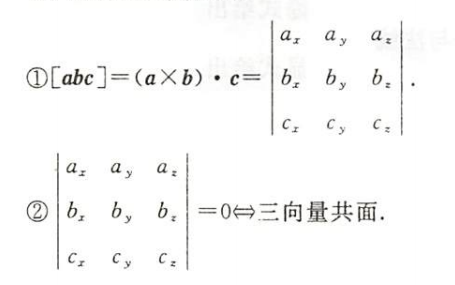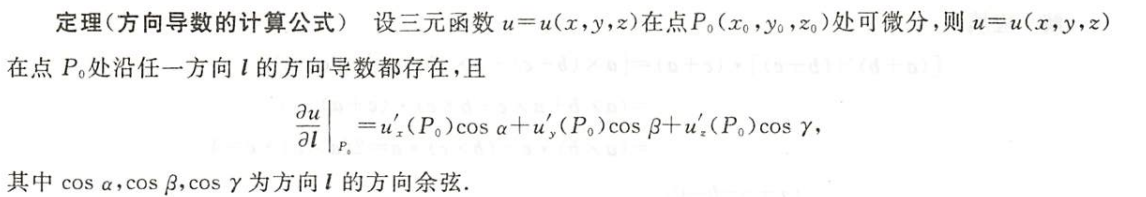zy2022
高等数学
多元函数积分学的基础知识
服务于第18讲
切一刀，转一周，投下来
向量代数
向量及其表达形式
向量的运算与应用
点积为零，垂直关系
数量积及其应用
向量积及其应用
混合积及其应用
向量的方向角和方向余弦
空间平面与直线
平面方程
一般式
点法式
三点式
截距式
直线方程
一般式
点向式
参数式
两点式
位置关系
距离
直线的关系
平面的关系
直线与平面的关系
空间曲线与曲面
空间曲线
一般式
参数方程
空间曲线在坐标面上的投影
- $\bigstar$ $\bigstar$ $\bigstar$
- 往哪个面投，就消去哪个字母
任意面，任意直线的投影：平面束
空间曲线与曲面
曲面方程
二次曲面
| 曲面名称 | 方程 | 图形 |
|---|---|---|
| 椭球面 | $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2}=1$ $\bigstar$ 注意球面:$x^2=y^2=z^2=a^2$ |  |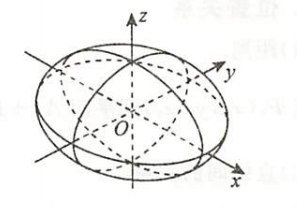
| 单叶双曲面 | $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2}=1$ |  |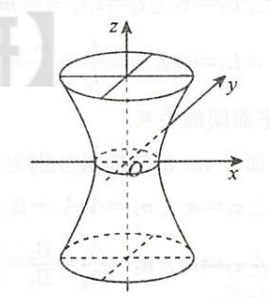
| 双叶双曲面 | $\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2}=1$ |  |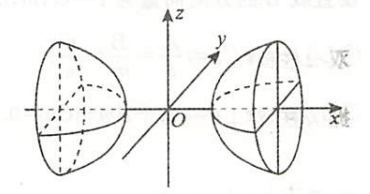
| 椭圆抛物面 | $\dfrac{x^2}{2p}+\dfrac{y^2}{2q}=z(p,q>0)$ $\bigstar$ 注意旋转抛物面:$x^2+y^2=z$ |  |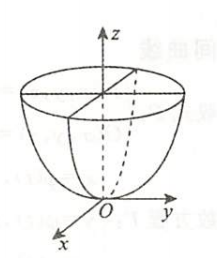
| 椭圆锥面 | $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = \dfrac{z^2}{c^2}$ $\bigstar$ 注意锥面:$z=\sqrt{x^2+y^2}$ |  |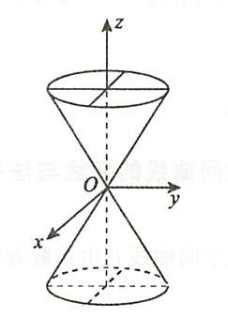
| 双曲抛物面(马鞍面)1 | $-\dfrac{x^2}{2p}+\dfrac{y^2}{2q}=z(p,q>0)$ |  |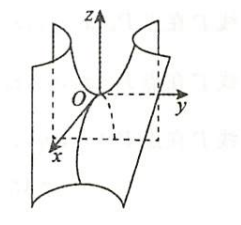
| 双曲抛物面(马鞍面)2 | $\bigstar$非常有趣 $z=xy$ |  |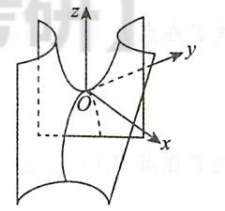
柱面
旋转曲面
- $\bigstar$ $\bigstar$
- 口诀
多元函数微分学的几何应用
空间曲线的切线与法平面
- 4分
参数方程给出
交面式方程给出
空间曲面的切平面与法线
- $\bigstar$ $\bigstar$ $\bigstar$
隐式给出
显式给出
场论初步
方向导数
- 在之前学的知识里面，偏导数也只是x轴，y轴，z轴方向上的变化率，并不涉及到任意方向上的变化率
梯度
方向导数与梯度的关系
散度
- $\sharp$ 解释再多最后也只是考一个公式
- 在一个点的发散程度
- 一道题就能解决问题，无非就是凑公式往里面套
选度
- 一道题就能解决问题，无非就是凑公式往里面套