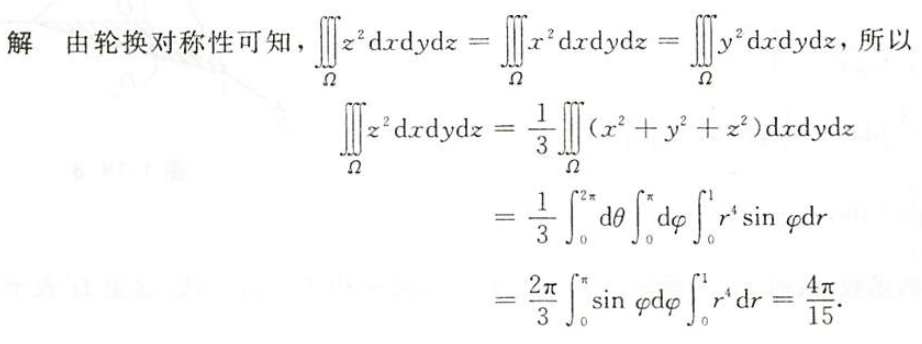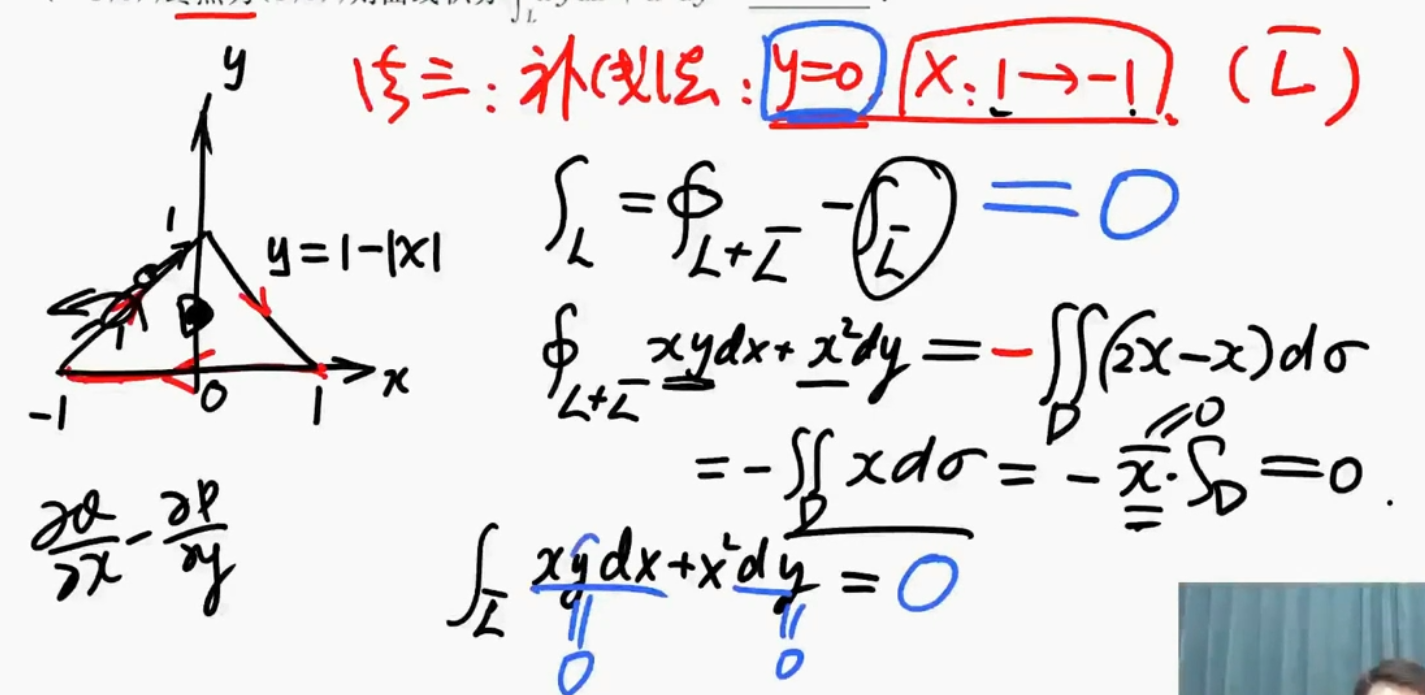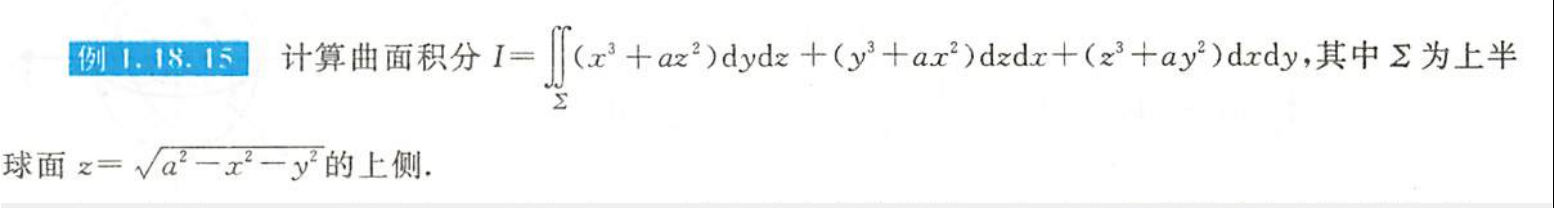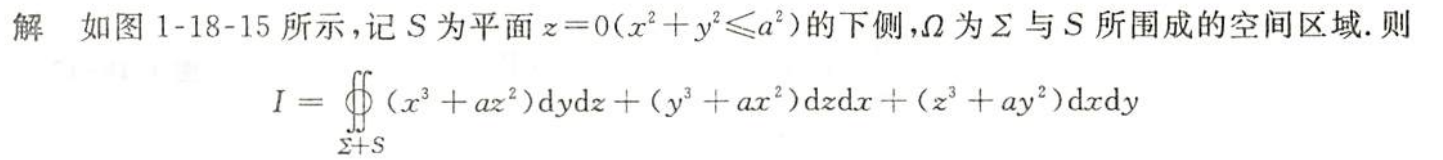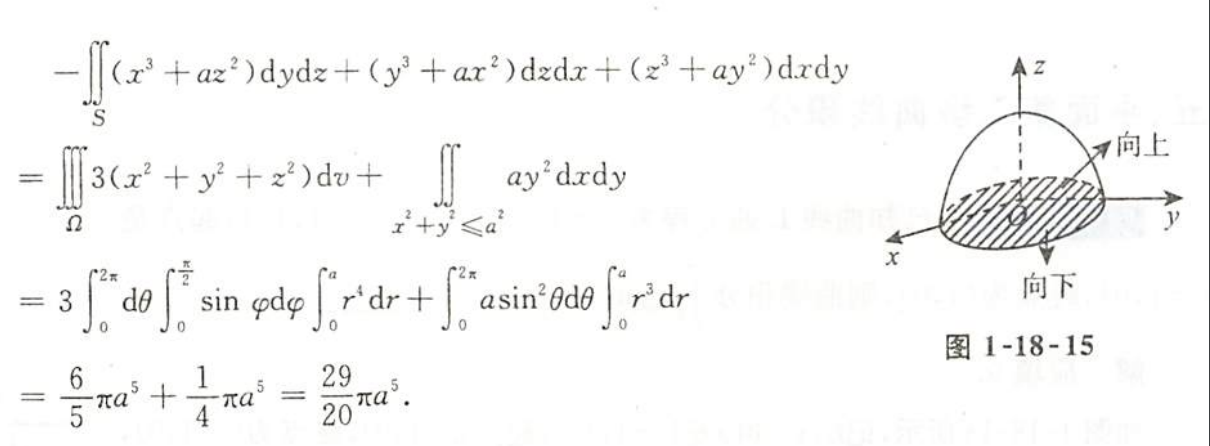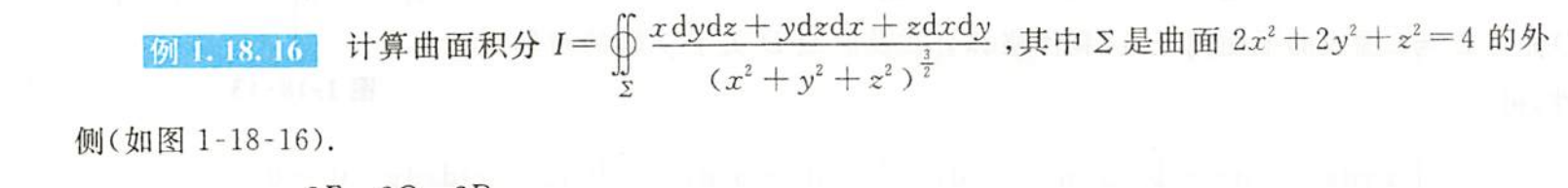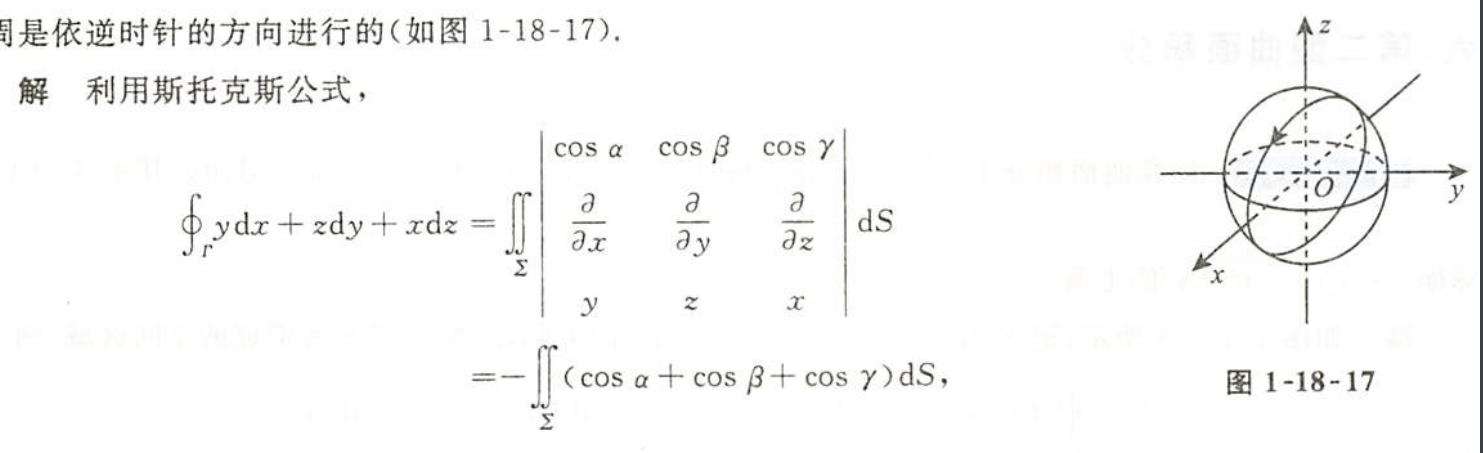凑数
凑数
凑数
凑数
题数统计
例1.18.1

解析
- 三重积分的基本方法
- 先1后2法,投影穿线法
- 写的时候写上谁的上限和下限,看的比较清楚
为什么没有面积定理:算错了,其实不是常数,不然是有的
求导公式的逆用积分用错
计算能力不行
总结
例1.18.2

解析

- 普通对称性
- 关于y对称
- 先二后一法
- 因为z相当于常数提走了
- z不在二重积分里面,可以用二重积分的面积性质
总结
例1.18.3

解析

$\mho$(为什么我的方法不对??)

总结
例1.18.4

解析

总结
例1.18.5

解析

总结
例1.18.6
解析
总结
例1.18.7
解析
总结
例1.18.8
解析
- 考研真题
- 普通对称性加轮换对称性
- $\blacktriangleright$(为什么不是x写成y和z的函数)
总结
例1.18.9
解析
总结
例1.18.10
解析
- $\bigstar$ $\bigstar$ $\bigstar$
- 对于对应投影部分的面积可以用上一讲的投影知识,投到哪个面就保留对应的字母
总结
例1.18.11
解析
总结
例1.18.13
解析
- 三种解法
- 第二型曲线积分
- 由对称性很容易得到结果是0
- 还可以用格林公式
格林公式的解法

总结
例1.18.14

解析

- 挖洞法下去回来了,抵消
- 积分与路径无关
- 椭圆的面积
- 永远取分母=一个常数
- $\pi ab$
总结
例1.18.15

解析


- 补面法,高斯公式
- “上侧”证明指定的正方向是上面
- 没有分母一阶偏导数一定连续
如果不用高斯公式怎么做
总结
例1.18.16

解析

总结
例1.18.17

解析


- 斯托克斯,z分量是正数
- 斯托克斯会有二型面积积分的问题
由斯托克斯有求一个平面的法向量即可,这时候直接求题目给的$x+y+z=0$的法向量
$$F=x+y+z \implies \overrightarrow{n}={F’_x,F’_y,F’_z}={1,1,1},F’_z\text{的正负需要额外考虑}$$
我居然是想用高中知识求法向量
总结
习1.18.17
解析
- 斯托克斯,z分量是负数
- 斯托克斯会有二型面积积分的问题
总结
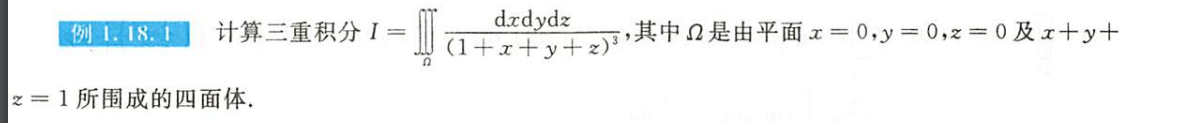


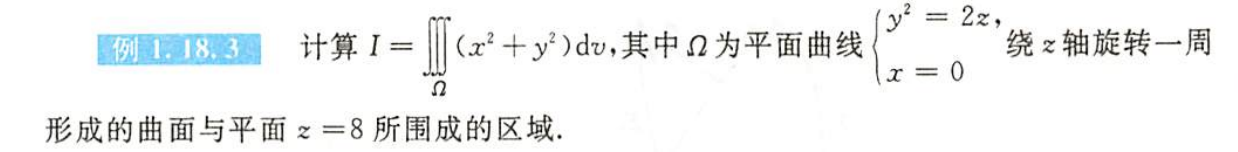

7R4%7EO2PUI42Y.jpg)