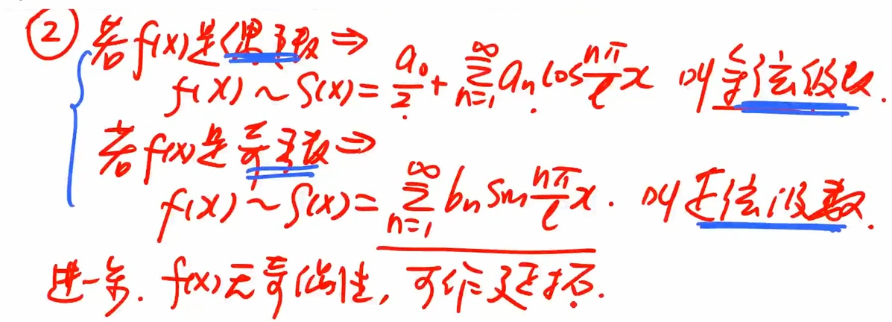zy2022
高等数学
数一专题内容(应用题)
一元函数微分学
- 没什么难点基本上都是套公式
- 投入产出比很高
物理应用
导数的物理意义,速度和加速度
相关变化率
- $\bigstar$ 5分 或 10分,必考无疑
几何应用
一元函数积分学应用
物理应用
相关变化率
- $\bigstar$ $\dfrac{dA}{dB}=\dfrac{dA}{dC}\cdot\dfrac{dC}{dB}$
几何应用
- 曲率公式:$k=\dfrac{|y\prime\prime|}{[1+(y\prime)^2]^{\frac{3}{2}}}$
- 曲率半径(曲率的倒数):$R=\dfrac{1}{k}=\dfrac{[1+(y\prime)^2]^{\frac{3}{2}}}{|y\prime\prime|}(y\prime\prime\neq0)$
一元函数积分学应用
物理应用
变力沿直线做功
抽水做功
$\bigstar$ 一直在猜会出这种题
水压力(静水压力)
- 2020
- 主要确定平板的宽度,
- $\blacktriangleright$(为什么只跟宽度有关系)
几何应用
“平面上的曲边梯形”的形心坐标公式
$\bar{x} = \dfrac{\int_a^bxf(x)dx}{\int_a^bf(x)dx}$
- $\blacktriangleright$ 推导过程,0到f(x)的积分为什么是f(x) :积分带进去就是了
$\bar{y} = \dfrac{1}{2}\dfrac{\int_a^bf^2(x)dx}{\int_a^bf(x)dx}$
平面曲线弧长
旋转曲面的表面积
平行截面为已知的立体体积
微分方程的物理应用
牛顿第二定律
- 表达式里可以不出现t
- $a=v\cdot\dfrac{dv}{dx}$
变化率问题
- $\bigstar$ $\dfrac{dA}{dB}$
- $\bigstar$ $\bigstar$ $\bigstar$ 传染病模型
欧拉方程
- 跟常系数微分方程作比较
傅里叶级数
- 送分题
- 展开为三角函数
- 对比展开为幂函数
${\textstyle\unicode{x2461}}$ 奇偶延拓
- 如果函数是偶函数,展开为余弦级数
- 如果函数是奇函数,展开为正弦级数
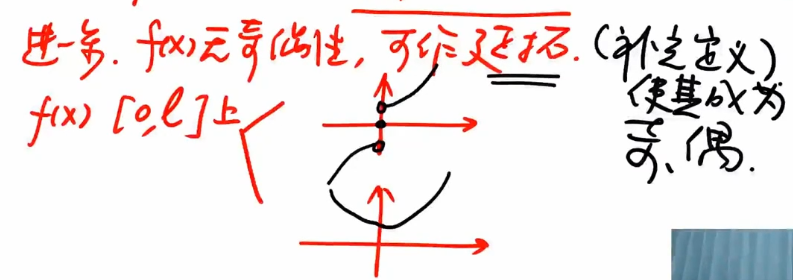
- 无奇偶性,可以作延拓(相当于补充定义)
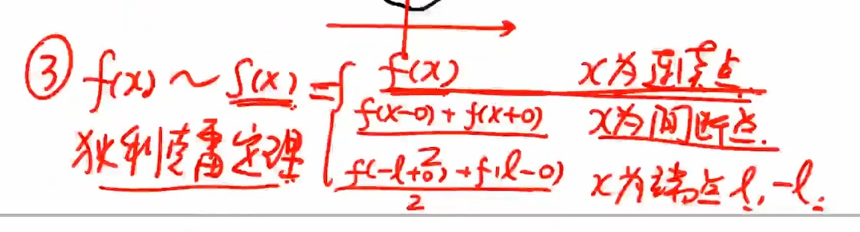
${\textstyle\unicode{x2462}}$ 迪利克雷收敛性定理
- 连续函数才相等,