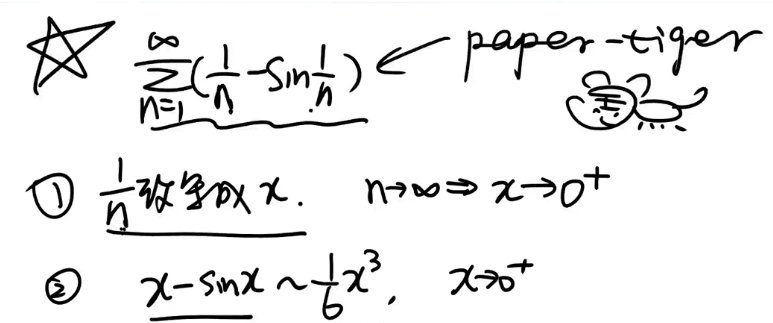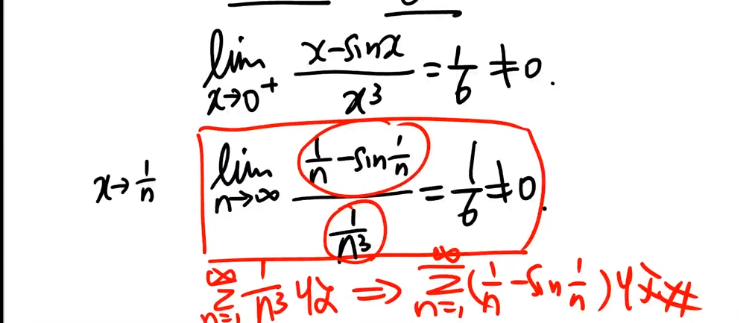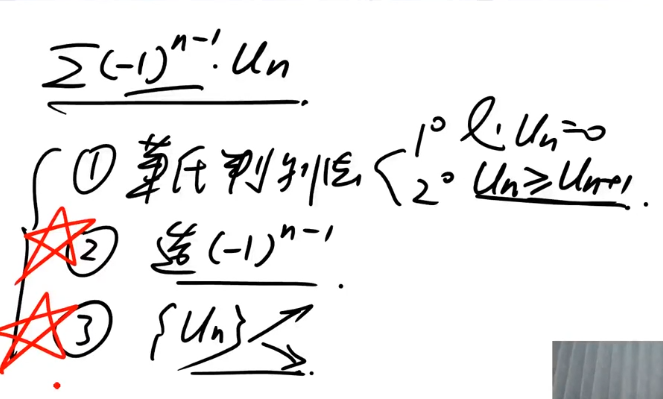zy2022

高等数学

无穷级数

主要是三类问题：判敛，求和，展开
可以和前面的不等式和数列极限配合着来看，把对应不等式的题目标记到对应知识点的旁边 $\mho$

常数项级数

常数项级数的概念与性质

引言

概念及其敛散性

给定一个无穷数列，将其各项用加号连起来得到的记号$\displaystyle \sum_{n=1}^{\infty}u_n$叫做无穷级数

${\textstyle\unicode{x2460}}$ 写$S_n$

${\textstyle\unicode{x2461}}$ 求$\displaystyle \lim_{n \to \infty}S_n$

性质

性质1 收敛级数的线性性质:两个级数收敛，求和必然收敛

性质2 改变级数任意有限项，不会改变该级数的敛散性

$\bigstar$ $\bigstar$ $\bigstar$ 性质3 如果级数收敛，通项必然趋于0

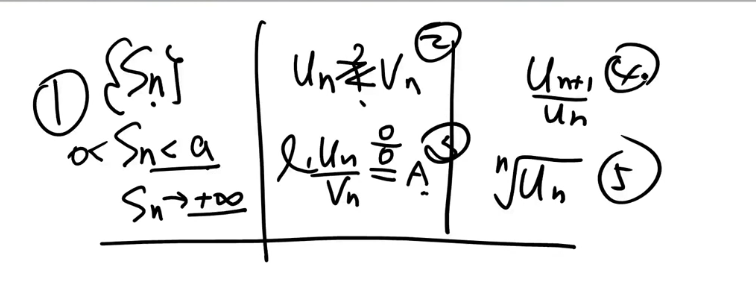
级数的敛散性的判别方法

4分或10分
5+1判别
两个概念（绝对收敛，条件收敛）

正项级数及其敛散性判别

一共五种方法

5+1(莱布尼茨)判别法

三个好朋友

p级数：p206注2
$\bigstar$ 广义p级数$\displaystyle \sum_{n=2}^{\infty}\dfrac{1}{n(lnn)^p}$,跟p级数的敛散性一致
等比级数 $\displaystyle \sum_{n=1}^\infty aq^{n-1} ,$
收敛原则
充分必要条件是它的部分和数列${S_n}$有界

比较判别法

两个正项级数，若大的收敛，则小的必收敛；若小的发散，则大的必发散

$\bigstar$ 比较判别法的极限形式

比阶

例子(讲了无数遍的等价无穷小替换)：

将每一项看成x

比值判别法(也叫达朗贝尔判别法)

$\bigstar$

后一项比前一项，的比值大于1发散，小于1收敛

用来解决形如 $a^n,n!,n^n$

根值判别法(也叫柯西判别法)

比较适合形如$a^n,n^n$,但是$n!$不考虑
交错级数及其敛散性判别
若级数正负相间出现，称这样的级数为交错级数

不能出现有0的项

莱布尼茨判别法

单调不增，且通项趋向于0，级数收敛

任意项级数及其敛散性判别

若级数各项可正，可负，可为零，称这样的级数为任意项级数

任意项=正向+交错级数

给任意项级数的每一项加上绝对值，写成$\displaystyle \sum{n=1}|u_n|$,这样，就使得$|u_n| \geq 0$,成了正项级数，它叫作原级数$\displaystyle \sum{n=1}^\infty$的绝对值级数

绝对收敛

条件收敛

本来是收敛的，加了绝对值就不收敛了

收敛级数的性质

性质4 收敛级数的项任意加括号后所得的新级数仍收敛,且其和不变.

性质5﹑若原级数绝对收敛,不论将其各项如何重新排列,所得的新级数也绝对收敛,且其和不变.(这个性质就是在说:绝对收敛的级数具有可交换性,此性质是德国数学家狄利克雷给出的.)

抽象级数的收敛问题 $\spadesuit$(p209:例1.14.11的注)

幂级数

幂级数及其收敛域

概念

图片详情

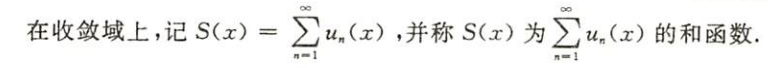
(1)函数项级数

(2)幂级数

(3)收敛点与发散点

(4) 收敛域

阿贝尔定理

当幂级数$\displaystyle \sum{n=0}^\infty a_nx^n\text{在点}x=x_1(x_1 \neq 0)\text{处收敛时，对于满足}|x|<|x_1|\text{的一切}x,\text{幂级数绝对收敛};\text{当幂级数}\displaystyle \sum{n=0}^\infty a_nx^n \text{在点}x=x_2(x_2 \neq 0)\text{处发散时，对于满足}|x|>|x_2|\text{的一切}x,\text{幂级数发散}$

但在对应的R点需要带进去用到之前的知识解决（端点处一定要单独讨论）

收敛域的求法

${\textstyle\unicode{x2460}}$ 求比值

${\textstyle\unicode{x2461}}$ 单独确定

$\bigstar$ $\spadesuit$(p210:原文) 求收敛域的统一方法【高数18讲（上面的课本方法缺项解决不了）】：$\sum u_n(x)$

${\textstyle\unicode{x2460}}\text{记}|u_n(x)| \geq 0$

${\textstyle\unicode{x2461}}\text{用}\displaystyle \lim{n \to \infty} \dfrac{|u{n+1}|(x)}{|u{n}|(x)}=\rho\text{或}\displaystyle \lim{n \to \infty}\sqrt{|u_n(x)|}=\rho,\text{令} \rho < 1 \implies x \in(a,b)$(收敛区间)

${\textstyle\unicode{x2462}}$单独讨论x=a，x=b的收敛性 $\implies$ 收敛域

$\bigstar$ $\mho$ $\spadesuit$(p210:具体内容) 抽象问题

条件收敛的情况是重要考点

幂级数求和函数

求和11分

概念

注：通过看书，发现只在收敛域上讨论和函数，所以x取值范围代表收敛域

运算法则

$\spadesuit$(p203:具体内容) 两个级数的下标相同，次数相同才能相加

通项、下标一起变
只变下标，不变通项
只变通项，不变下标

性质

重要展开式