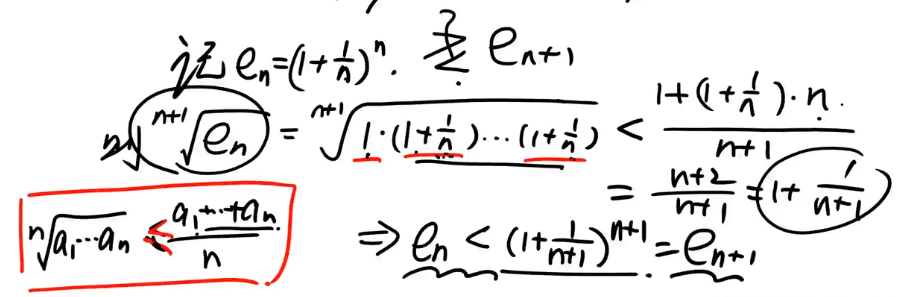0%
凑数
凑数
凑数
凑数
例1.14.2
解析
- 根据p级数的概念迅速证明
- 放缩之后无界根据必要条件,必然发散
- 证明发散就放小,证明收敛就放大
总结
例1.14.3
解析
- 调和级数(导数的平均值为另外一个人的倒数)
- 级数对不等式的要求比较高
- $x>ln(1+x)$
总结
例1.14.6
解析
- $\bigstar$(考研的味道)
- 用不等式解决问题
- 大的收敛小的必收敛
总结
例题1.14.4
解析
- 达朗贝尔判别法
- ${(1+\dfrac{1}{n})^n}$是单调增加趋向e
总结
例1.14.5
解析
- 柯西判别法
- sinx-x和幂值函数的处理
- 相当于$\dfrac{1}{n}$次方,约掉一个
总结
例1.14.7
解析
总结
例1.14.8
解析
- $\bigstar$(非常经典的例子)
- 莱布尼茨判别法
总结
例1.14.10
解析
总结
例题1.14.11
解析
- $\bigstar$(考研风格)
- 积累
- 做题当中积累和学习(很像写代码,再写代码中学习和积累)
总结
例题1.14.13
解析
总结
例1.14.14
解析
- $\bigstar$(热门考点)
- 麻雀虽小五张俱全的题
总结
例1.14.15
解析
- 经典的题目
- 需要转为定积分或者变上限积分没不然要确定常数C
- n在分母上,先导后积(视频的先导后积公式的推导也在这里)
- $S(x)=S(x_0)+\int_{x_0}^xS’(t)dt$
- $\blacktriangleright$(为什么只能限定|t|<1)
总结
例1.14.16
解析
总结
例1.14.17
解析
- $\bigstar$(奇数年的考题风格)
- 相当于$\dfrac{1}{1+t^2}$的原因要知道
总结
例1.14.18
解析
总结