zy2022
高等数学
二重积分
- 分值分布
- 5分+11分大题
概念、性质与对称性
几何背景
性质
性质1(求区域面积)
性质2(可积函数必有界)
性质3(积分的线性性质)
性质4(积分的可加性)
性质5(积分的保号性)
性质6(二重积分的估值定理)
性质7(二重积分的中值定理)
$\bigstar$(5分) 对称性
普通对称性
图片详情

轮换对称性
图片详情

- $x$和$y$对调之后,区域D不变
- 积分值与字母无关(谁动了我的面包)
- 轮换是指字母对换,对称是指区域不变
- 直角坐标系才能用
计算
直角坐标系
后积先定限,限内画条线,先交写下限,后交写上限
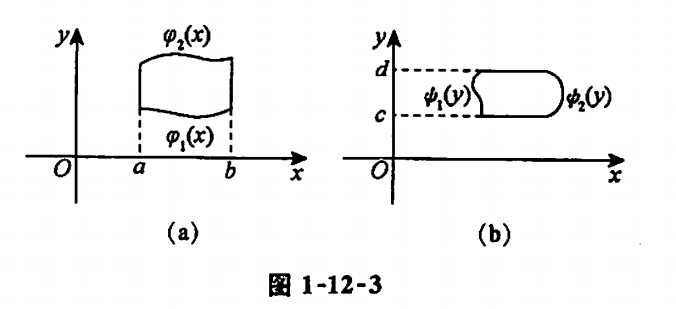
(1) X型区域(上下型)(a图)
- 可以理解为限内的线在X轴上运动,所以叫X型区域,后积X
$$
\displaystyle \iint_Df(x,y)d\sigma = \int_a^bdx\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy,\text{其中}D\text{为}X\text{型区域:}\varphi_1(x)\leq y\leq\varphi_2(x),a\leq x\leq b
$$
(2) Y型区域(左右型)(b图)
- 可以理解为限内的线在Y轴上运动,所以叫Y型区域,后积Y
$$
\displaystyle \iint_Df(x,y)d\sigma = \int_c^ddx\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)dx,\text{其中}D\text{为}Y\text{型区域:}\psi_1(y)\leq x\leq\psi_2(y),c\leq y\leq d
$$
极坐标系
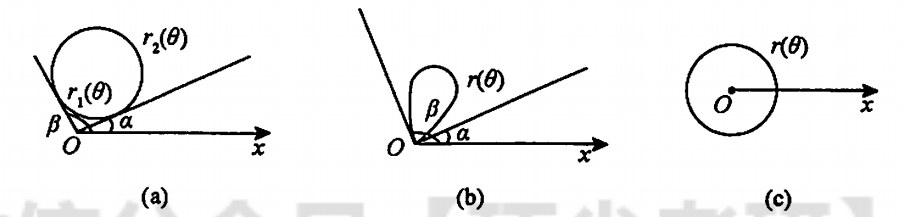
(1)极点O在区域D外部(a图)
$$
\displaystyle \iint_Df(x,y)d\sigma = \int_\alpha^\beta d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(rcos\theta,rsin\theta)rdr
$$
(2)极点О在区域D边界上(b图)
$$
\displaystyle \iint_Df(x,y)d\sigma = \int_\alpha^\beta d\theta\int_0^{r(\theta)}f(rcos\theta,rsin\theta)rdr
$$
(3)极点O在区域D内部(c图)
$$
\displaystyle \iint_Df(x,y)d\sigma = \int_0^{2\pi}d\theta\int_0^{r(\theta)}f(rcos\theta,rsin\theta)rdr
$$
在极坐标系下,几乎所有的计算都是先积$r$,后积$\theta$,所以一般不讨论积分次序的交换问题
极坐标系与直角坐标系的选择的一般原则
- ${\textstyle\unicode{x2460}}$ 看被积函数的形式:$f(x^2+y^2),f(\dfrac{y}{x}),f(\dfrac{x}{y})$
- ${\textstyle\unicode{x2461}}$ 积分区域是否是圆(主要看 ${\textstyle\unicode{x2460}}$ )
极直互化
- 极坐标系和极坐标系的互换
- 上下限反解xy
$$
\begin{cases}
x=r cos\theta , & \cr
y=r sin\theta , &
\end{cases}
$$
积分次序
- 先积分x还是y
用二重积分处理一元积分的问题
- 特色