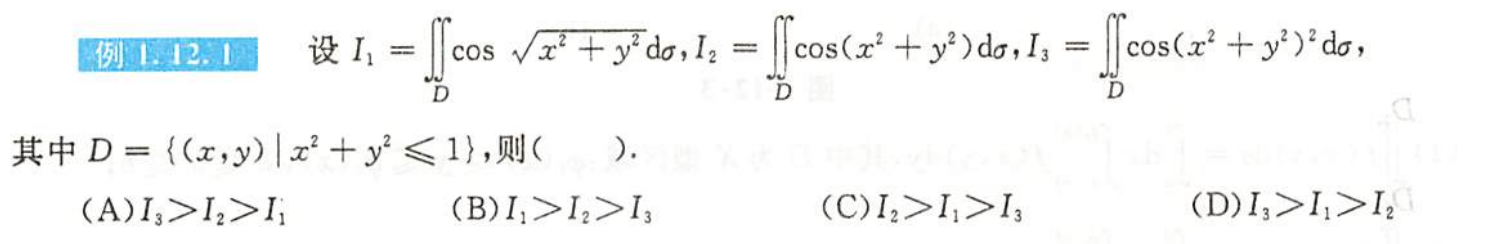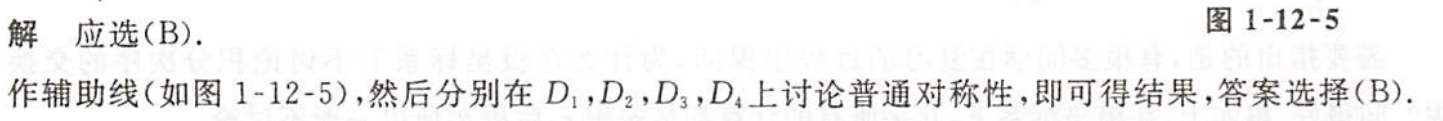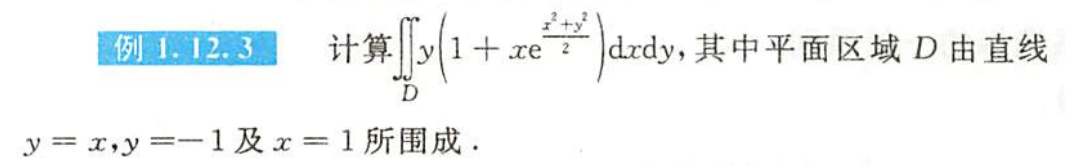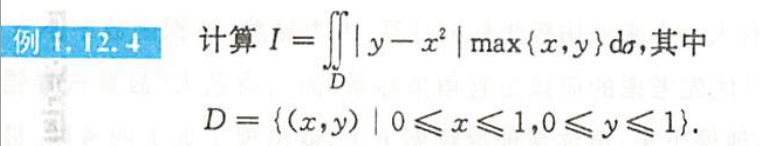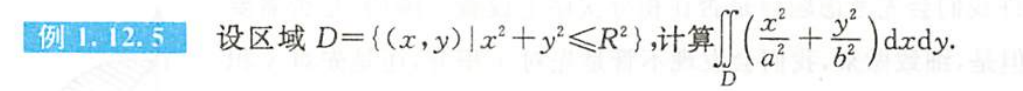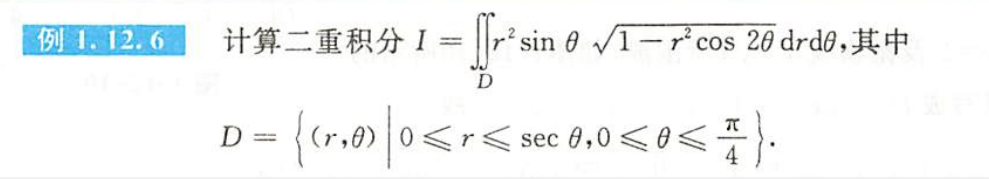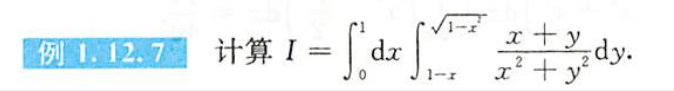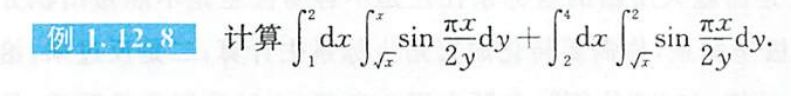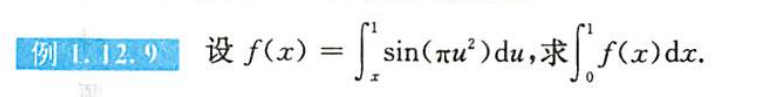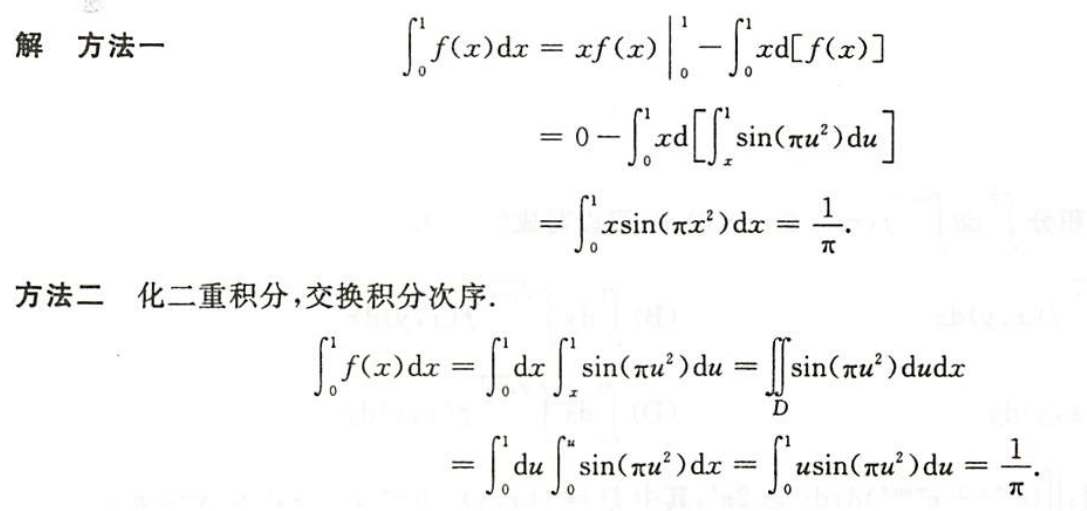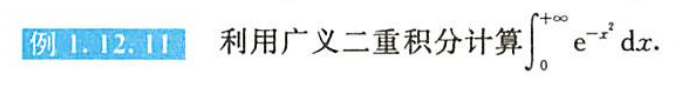凑数
凑数
凑数
凑数
二重积分题目说明
| 位置 | 题数 |
|---|---|
| 例题 | 11 |
| 课后习题 | 7 |
| 300题 | 9 |
例题1.12.1
解析
- 保号性
- 幂函数的比较
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例1.12.2
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例题1.12.3
解析
- 普通对称性
- $\bigstar$(麻雀虽小五章俱全)
- 能拆则拆
- 直角坐标系上的积分
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 没有考虑被积函数的正负 | true |
例1.12.4
解析
思路很清晰，一定是分情况讨论
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 算错数 | false |
例题1.12.5
解析
- r跟R不一样
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 写错答案 | true |
例1.12.6
解析
- 极坐标系换成直角坐标系
- $\blacktriangleright$(题目出错了？) x\text{应该小于}cos \theta$,没错，导数刚好就是阴影部分
- 二重积分别样的凑微分法
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例题1.12.7
解析
- $\flat$
- 命题老师往往会帮倒忙，他写成dxdy可能要转换为rdr
- 用$\text{积分下限}1-x \implies x+y=1 \implies rcos\theta + rsin\theta=1$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例题1.12.8
解析
- $\bigstar$
- 常见：有原函数但求不出初等函数形式的原函数
- $\int \dfrac{sinx}{x}dx,\int \dfrac{cosx}{x}dx,\int \dfrac{tan x}{x}dx,\int \dfrac{e^x}{x}dx,sin\dfrac{1}{x},cos\dfrac{1}{x}$
- $\int sin x^2 dx,\int cos x^2 dx,\int tan x^2 dx,$
- $\int e^{ax^2+bx+c}dx (\int e^{x^2} dx,\int e^{-x^2} dx,)$
- $\int \dfrac{dx}{lnx}dx$
- 椭圆函数
- 交换积分次序
- 注意还要配方
- 注意正负，最好让所有的元素都出现在表格中操作
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例1.12.9
解析
- $\bigstar$ $\bigstar$ $\bigstar$
- 化一元积分为二重积分，交换积分次序
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例1.12.10
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 | false |
例1.12.11
解析
- $\bigstar$ 结果也很重要
- 广义的圆
- 高斯曲线的积分值为$\dfrac{\sqrt{\pi}}{2}$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |