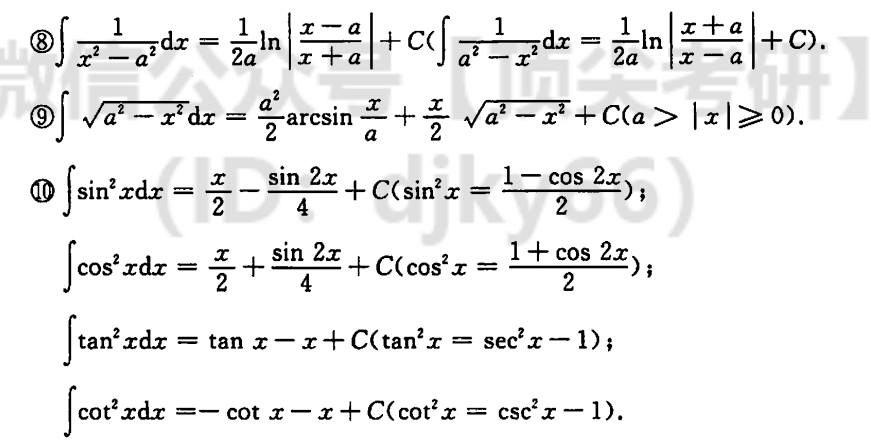zy2022

高等数学

一元函数积分学的概念与计算

02是第二个视频t是时间

祖孙三代:积分，原函数，导数
- $\int_a^x e^{t^2}dt \leftarrow e^{x^2} \rightarrow e^{x^2} \cdot 2x$
- 考研常考：$\int_0^x e^{t^2}dt$,0做下限，按照函数奇偶性(todo)，原函数是偶函数只有其0下限的变限积分是奇函数,证明($\dagger$(1.8.6))
- $\flat$(02 t=00:35:37.362) 周期性

2021.4.30 后面傅里叶的时候讲到$int_a^x f(x)dt$ 就不带常数没听懂

概念

不定积分

原函数与不定积分

设函数$f(x)$定义在某区间$I$上,若存在可导函数$F(x)$，对于该区间上任意一点都有$F’(x)=f(x)$成立，则称 $F(x)$是$f(x)$在区间$I$上的一个原函数,称$\int f(x)dx=F(x)+C$为$f(x)$在区间$I$上的不定积分,$C$为任意常数

原函数存在定理

(1) 连续函数$f(x)$必有原函数$F(x)$

(2) 含有第一类间断点、无穷间断点的函数$f(x)$在包含该间断点的区间内必没有原函数$F(x)$

含有震荡间断点的函数有原函数
导数介值定理可证
$\bigstar$(结构性知识总结) 考研中的五种点
- 连续点
- 跳跃点
- 可去间断点
- 无穷间断点
- 震荡点

定积分

定积分是个数,变限积分是函数

定积分的概念

$$
\int_a^b f(x)dx=\displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=1}^nf(a+\dfrac{b-a}{n}i)\dfrac{b-a}{n}
$$

$$
\spadesuit\text{(p125:重点)} \text{取}a=0,b=1,\displaystyle \lim_{n \to \infty} \sum_{i=1}^nf(\dfrac{i}{n})\dfrac{1}{n}=\int_0^1f(x)dx
$$

用定积分的定义解决题目的方法
- ${\textstyle\unicode{x2460}}$ 先提出$\dfrac{1}{n}$
- ${\textstyle\unicode{x2461}}$凑出$\dfrac{i}{n}$
- 写出$\int_0^1f(x)dx$

$\bigstar$(结构性知识总结)基础30讲学基本的方法，推导，强化训练解决怪物的各种变形和形式，基础班相当于塞尔达的普通模式，强化班相当于塞尔达的大师模式(题目综合性强(怪物的组合更加综合)，血量变厚(综合，复杂))

定积分存在定理

$\blacktriangleright$(这些充分条件是交的关系还是并的关系:2021.4.30感觉是并的关系，充分条件本身就是小范围的条件，每一个点的则也能够看出来)

(1) 定积分存在的充分条件

${\textstyle\unicode{x2460}} \text{若} f(x)\text{在}[a,b]\text{上连续,则}\int_a^b f(x)dx\text{存在}$

${\textstyle\unicode{x2461}} \text{若} f(x)\text{在}[a,b]\text{上单调,则}\int_a^b f(x)dx\text{存在}$

${\textstyle\unicode{x2462}} \text{若} f(x)\text{在}[a,b]\text{上有界,且只有有限个间断点,则}\int_a^b f(x)dx\text{存在}$

(2) 定积分存在的必要条件

可积函数必有界，即若定积分$\int_a^b$ 存在,则$f(x)\text{在}[a,b]\text{上必有界}$

定积分的性质

假设积分均存在

性质1(求区间长度)

$\text{假设}a<b,\text{则}\int_a^bdx=b-a=L,\text{其中}L\text{为}\text{区间}[a,b]\text{的长度}$

性质2(积分的线性性质)

$\text{设}k_1,k_2\text{为常数,则}\int_a^b[k_1f(x) \pm k_2g(x)]dx=k_1\int_a^bf(x)dx\pm k_2\int_a^b g(x)dx$

性质3(积分的可加(拆)性)

$\text{无论}a,b,c\text{的大小如何,总有}\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx$

性质4(积分的保号性)

$\text{若在区间}[a,b]\text{上}f(x)\leq g(x)\text{,则有}\int_a^bf(x)dx\leq \int_a^bg(x)dx$

特殊地，有$|\int_a^bf(x)dx|\leq\int_a^b|f(x)|dx$(积分的绝对值小于等于绝对值的积分)

性质5(估值定理)

$\text{设}M,m\text{分别是}f(x)\text{在}[a,b]\text{上的最大值和最小值，}L\text{为区间}[a,b]\text{的长度,则有}mL\leq\int_a^bf(x)dx\leq ML$

$\bigstar$ $\bigstar$ $\bigstar$ 性质6(中值定理) $\text{设}f(x)\text{在闭区间}[a,b]\text{上连续，则在}[a,b]\text{上至少存在一点}\xi\text{,使得}\int_a^bf(x)dx=f(\xi)(b-a)$

拉格朗日证:令$F(x)=\int_a^xf(t)dt$

变限积分

变限积分的概念

变限积分就是定积分的推广
变限积分 $\int_a^xf(t)dt=F(x)$,$F(x)\text{就是}f(t)\text{的一个原函数}$(证明)

变限积分的性质

(1) $\text{函数}f(x)\text{在}[a,b]\text{上可积,则函数}F(x)=\int_a^xf(x)dx\text{在}[a,b]上连续$

(2) $\text{函数}f(x)\text{在}[a,b]\text{上连续,则函数}F(x)=\int_a^xf(x)dx\text{在}[a,b]上可导$

只要变限积分存在，变限积分就必定是连续的

如果函数$f(x)\text{在}[a,b]\text{上连续，则函数}F(x)=\int_a^xf(t)dt\text{在}[a,b]\text{上可导,且}F\prime(x)=f(x)$(证明)

变限积分的求导公式

$$
F\prime(x)=\dfrac{d}{dx}[\int_{\varphi_1(x)}^{\varphi_2(x)}f(t)dt] = f[\varphi_2(x)]\varphi\prime_2(x) - f[\varphi_1(x)]\varphi\prime_1(x)
$$

【注】︰我们称上面公式中的x为“求导变量”,t为“积分变量”.“求导变量”x只出现在积分的上、下限时才能使用变限积分求导公式,若“求导变量”x出现在被积函数中,必须通过恒等变形(比如变量代换等),将其移出被积函数,才能使用变限积分求导公式.

反常积分

区间长度无限
或者有无穷大的值

反常积分概念的通俗理解

将b和$\infty$带到积分上去算，算出来收敛，算不出来发散

$\mho$(例子的求和极限没看懂)

$$\int_a^{+\infty}f(x)dx\text{收敛不一定能推出}\displaystyle \lim_{x \to +\infty}=0$$

(上限无穷大的变限积分收敛不代表原函数趋于无穷的极限为0)

无穷区间上反常积分的概念与敛散性

在反常积分中，一般把“$\infty$”和使得函数极限为无穷的点(瑕点)统称为奇点.

无界函数的反常积分的概念与敛散性

如果函数f(x)在点a的一个邻域内无界，那么点a称为函数f(x)的 $\color{green}{\text{瑕点}}$

判敛

$\bigstar$ 计算

$\bigstar$(知识结构)考研数学三大计算
- 极限
- 求导
- 求积

基本积分公式

换元三换
- 积分元素
- 积分上下限
- 被积函数

凑微分法

(1) 基本思想 $\int f[g(x)]g’(x)dx=\int f[g(x)]dg(x)=\int f(u)du$

也叫第一类换元法

题目：(1，2)

换元法

(1) 基本思想 $\int f[g(x)]g’(x)dx=\int f[g(x)]dg(x)=\int f(u)du$

举重若轻
倒代换，高次放上面，不稳定容易动
- 倒代换的适用范围

(2)思维结构

$\mho$(记得讲过换元法的技巧，比如见到x^2怎么换元什么的，补充一下)
分部积分法
(1) 基本思想 $\int udv=uv-\int vdu$
积分简单当v，求导简单那当u
反对幂指三(越左越$u$，越右越$v$)
- v被积分，u被求导
- 这个顺序刚好对应表格法的上下顺序，越左越上，越右越下

$\sharp$ 自己简化课本的知识让自己理解

$\spadesuit$(p112:注) 分部积分的推广公式，分部积分表格

有理函数积分

$\bigstar$(考前可能会忘掉)

直接用特殊值法求值

定积分的计算

用牛顿莱布尼茨公式，能带值代值，不能带值取极限

如果是找原函数的话，就是在考不定积分的能力，反之研究性质 $\spadesuit$(p114:注)

注4重点：区间在重现公式(别样换元法)
- $f(x)+f(a+b-x)$
注5年年考：点火公式
- 三个重要的结论

定积分的换元积分法

定积分的分部积分法

基本积分表

公式	题目
$\int x^kdx=\dfrac{1}{k+1}x^{k+1}+C,k\neq-1$
$\int \dfrac{1}{x^2}dx=-\dfrac{1}{x}+C$
$\int \dfrac{1}{\sqrt{x}}dx=2\sqrt{x}+C$
$\int \dfrac{1}{x}dx=ln\lvert x\rvert+C$
$\int e^xdx=e^x+C$
$\int a^xdx=\dfrac{a^x}{ln a}+C,(a >0 \text{且} a \neq 1)$
$\int e^xdx=e^x+C$
$\int sinxdx=-cosx+C$
$\int cos xdx=sin x+C$
$\int tan xdx=-ln\lvert cos x \rvert+C$
$\int cot xdx=ln\lvert sin x \rvert+C$
$\int\dfrac{dx}{cosx}=\int secxdx=ln\lvert secx+tanx \rvert+C$	1
$\int\dfrac{dx}{sinx}=\int cscxdx=ln\lvert cscx-cotx \rvert+C$
$\int sec^2xdx=tanx+C$
$\int csc^2xdx=-cotx+C$
$\int secxtanxdx=secx+C$
$\int cscxcotxdx=-cscx+C$
$\int \dfrac{1}{1+x^2}dx=arctanx+C$
$\int \dfrac{1}{a^2+x^2}dx=\dfrac{1}{a}arctan\dfrac{x}{a}+C$
$\int\dfrac{1}{\sqrt{1-x^2}}dx=arcsinx+C$
$\int\dfrac{1}{\sqrt{a^2-x^2}}dx=arcsin\dfrac{2}{a}+C$
$\int\dfrac{1}{\sqrt{x^2+a^2}}dx=ln(x+\sqrt{x^2+a^2})+C(\text{常见}a=1)$
$\int\dfrac{1}{\sqrt{x^2-a^2}}dx=ln\lvert x+\sqrt{x^2+a^2} \rvert+C(\lvert x\rvert>\lvert a \rvert)$
$\int\dfrac{1}{x^2-a^2}dx=\dfrac{1}{2a}ln\lvert \dfrac{x-a}{x+a} \rvert+C(\int \dfrac{1}{a^2-x^2}dx=\dfrac{1}{2a}ln\dfrac{\lvert x+a \rvert}{\lvert x-a \rvert}+C)$
$\int\sqrt{a^2-x^2}dx=\dfrac{a^2}{2}arcsin\dfrac{x}{a}+\dfrac{x}{2}\sqrt{a^2-x^2}+C$
$\int sin^2xdx=\dfrac{x}{2}-\dfrac{sin 2x}{4}+C(sin^2x=\dfrac{1-cos2x}{2})$
$\int sin^2xdx=\dfrac{x}{2}+\dfrac{sin 2x}{4}+C(cos^2x=\dfrac{1+cos2x}{2})$
$\int tan^2xdx=tanx-x+C(tan^2x=sec^2x-1)$
$\int cot^2xdx=-cotx-x+C(cot^2x=csc^2x-1)$

$\mho$(华理士公式(点火公式)也要补充在这里面)

$${\textstyle\unicode{x2461}} \int\dfrac{1}{x}dx=ln|x|+C$$

题目：(1)

$$
{\textstyle\unicode{x2465}} \begin{cases}
\int \dfrac{1}{\sqrt{1-x^2}}dx = arcsin x + C , & \cr
\int \dfrac{1}{\sqrt{a-x^2}}dx = arcsin \dfrac{x}{a} + C(a>0) . &
\end{cases}
$$

题目：(1，)

$$
{\textstyle\unicode{x2468}} \int\sqrt{a^2-x^2}dx=\dfrac{a^2}{2}arcsin\dfrac{x}{a}+\dfrac{x}{2}\sqrt{a^2-x^2}+C
$$

题目：(1:推导)

ednow

高等数学-ch8-一元函数积分学的概念与计算