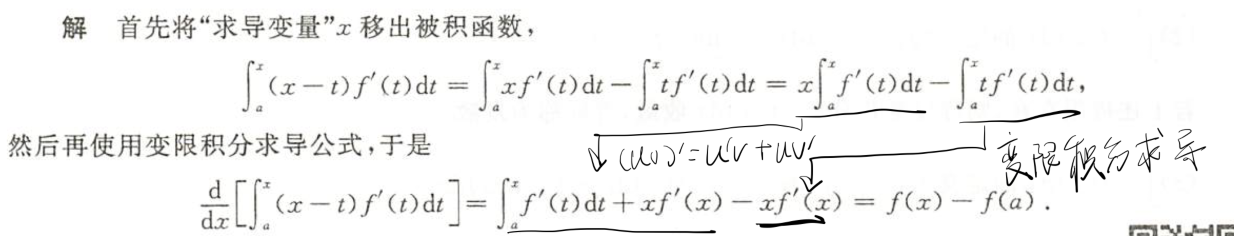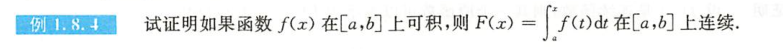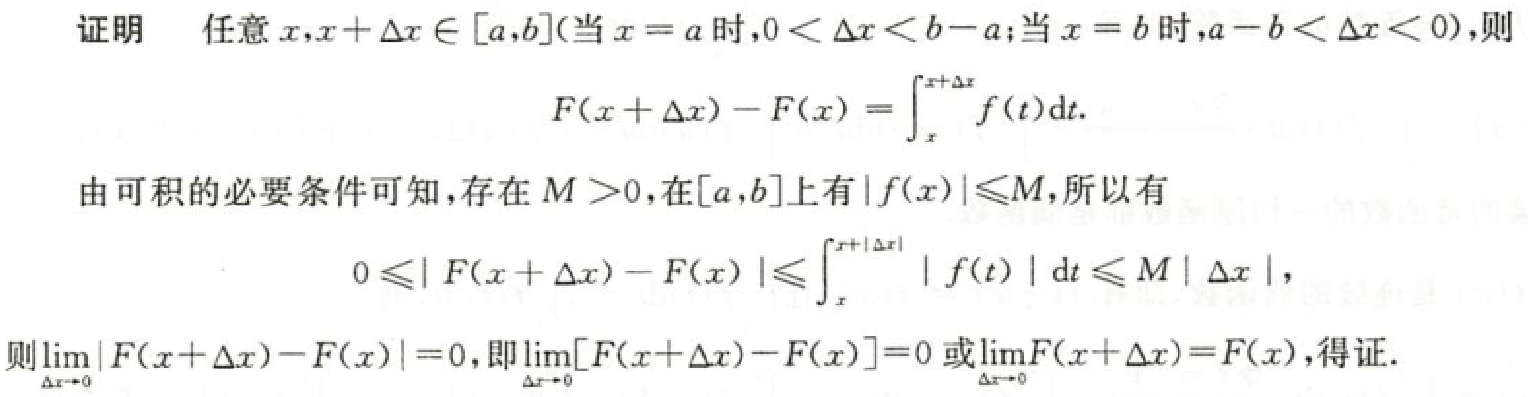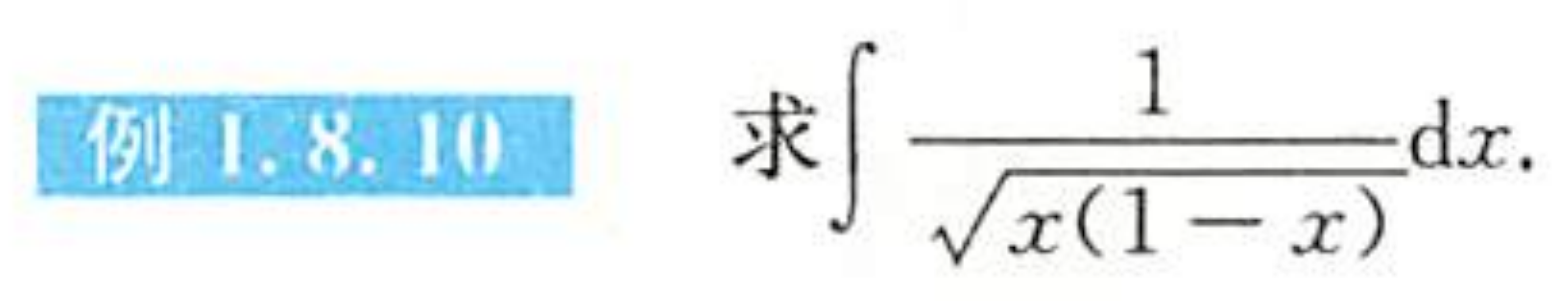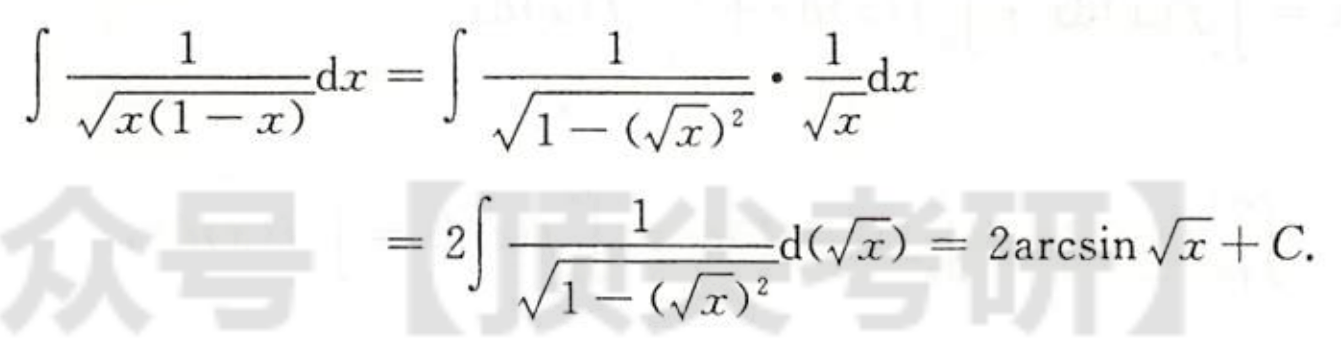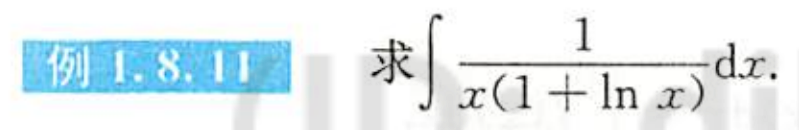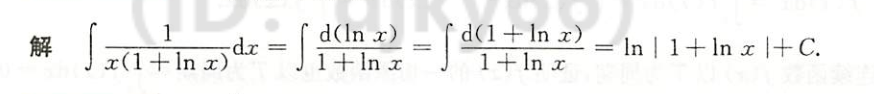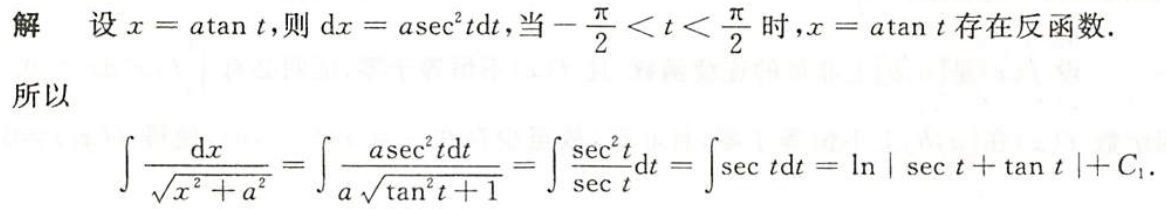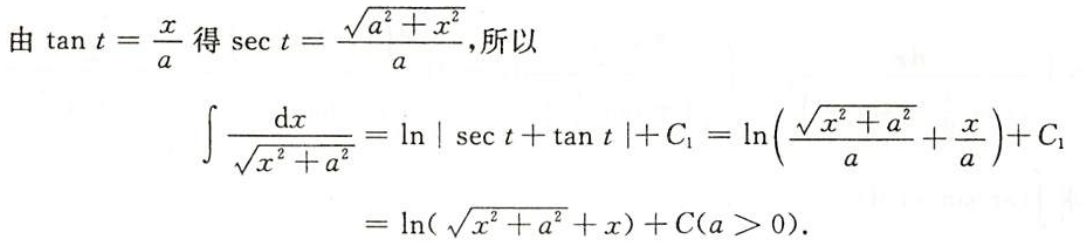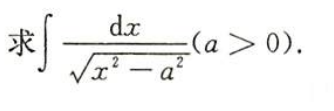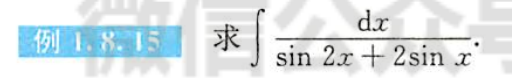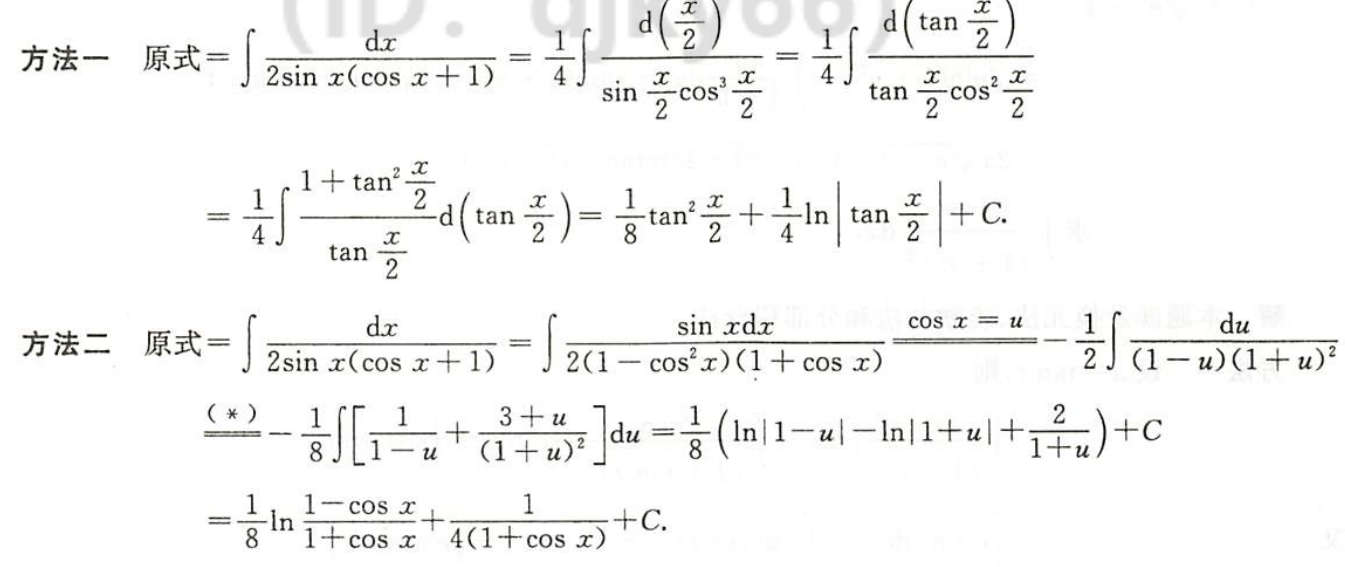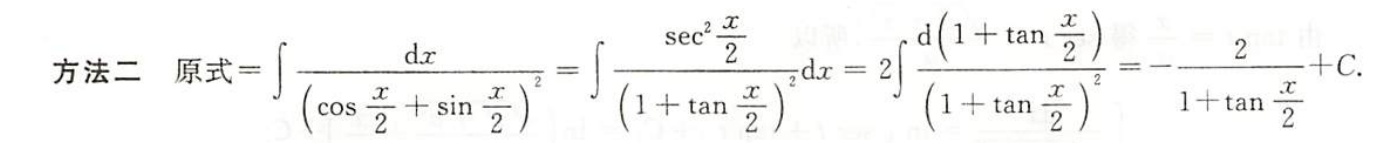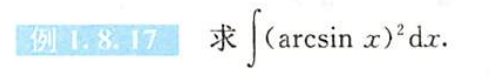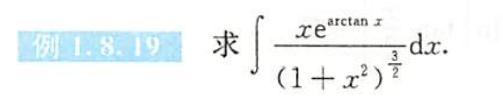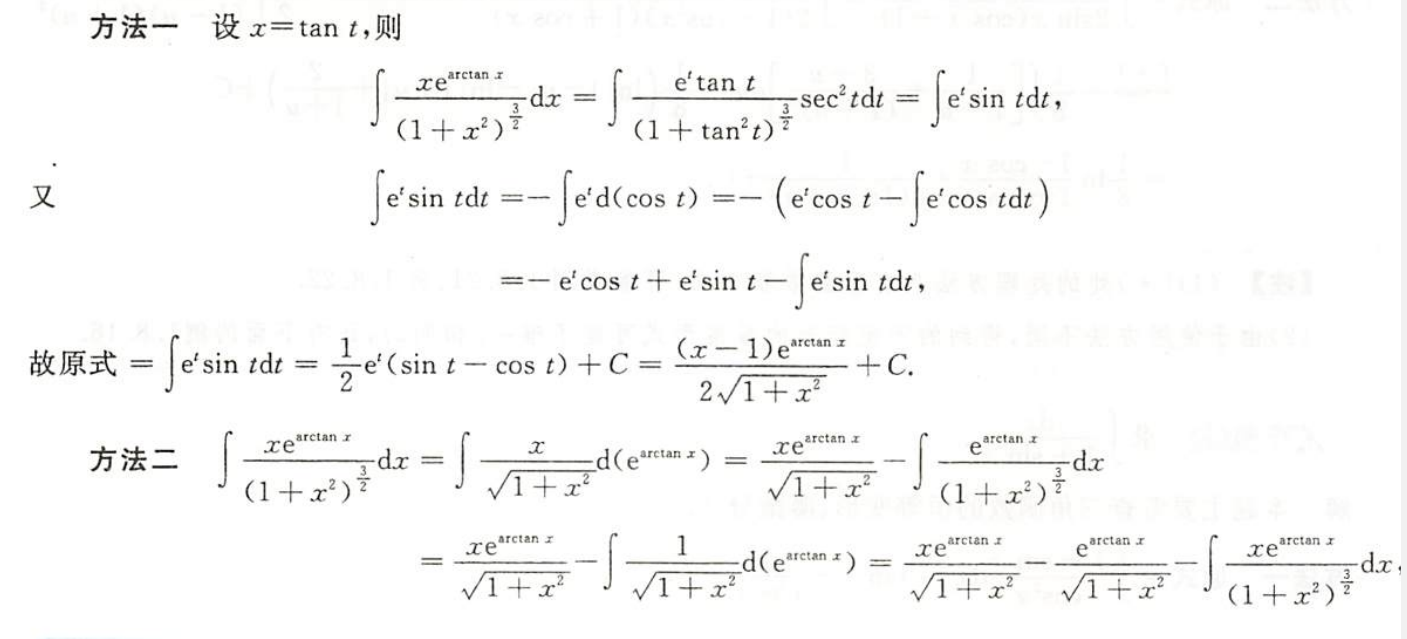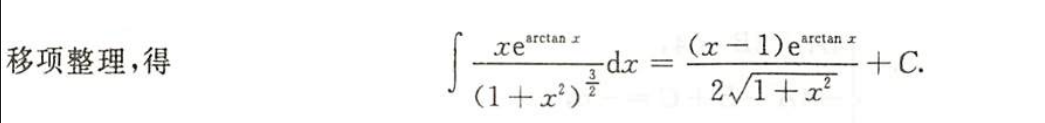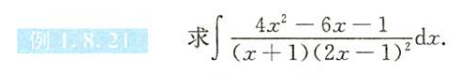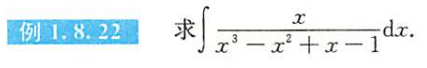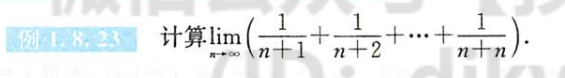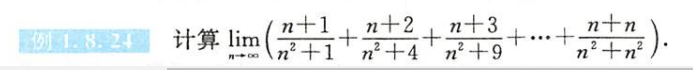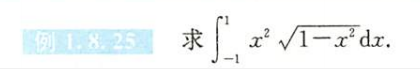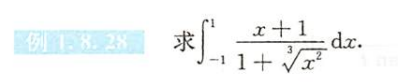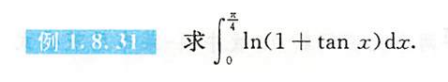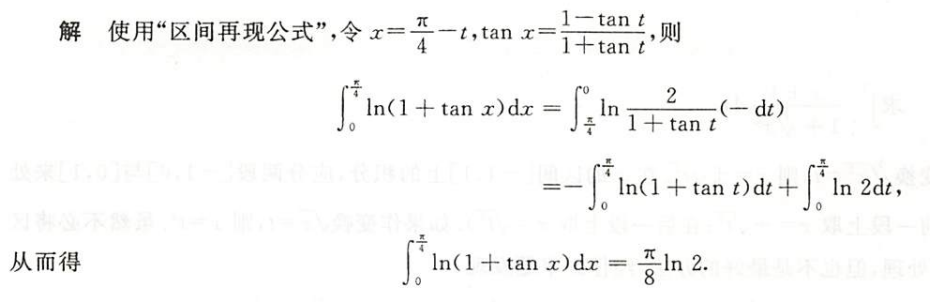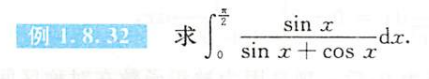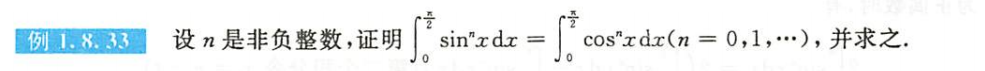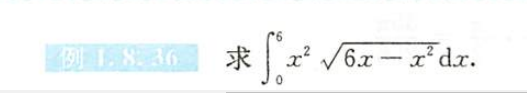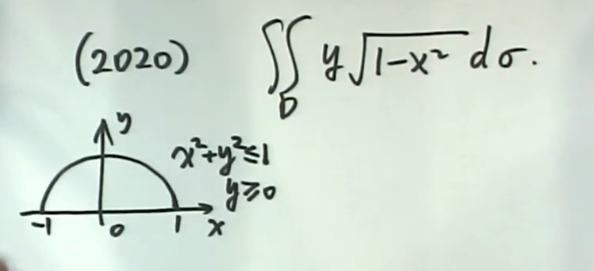凑数
凑数
凑数
凑数
注
[1.8.6,1.8.9]都没做，都是证明题，之后重新回来再做先做计算题
本节例题49道，课后题21道，300题14道，一共84道题
尚有题未总结
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
变限积分求导时x出现在被积函数中
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
上限无穷大的变限积分收敛不代表原函数趋于无穷的极限为0
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例题1.8.1
解析
- 积分中值定理
- $\blacktriangleright$(本来积分中值定理就是闭区间，他怎么变成开区间了，感觉步骤有问题，教材怎么写的)
- 凑导数的定义$\displaystyle \lim_{\Delta x\to 0}\dfrac{\Delta F}{\Delta x}$
思路：
联系 F(x) 和 F$\prime$(x)的方法：积分中值定理
积分可拆性凑出积分中值定理，用定义约掉$\Delta x$
出现F$\prime \prime$(x)的方法，三次罗尔中值定理,两次拉格朗日中值定理，泰勒展开到二阶
题型: 证明题
错因: 超越理解范围
教训:
上课的时候应该把思路记下来
例题1.8.2
解析
- 导数介值定理
思路
肯定是反证法
导数的定义+洛必达
题型:
错因:
教训:
例1.8.3
解析
$(uv)\prime = u\prime v+v\prime u$
原函数和定积分存在定理的使用
$\blacktriangleright$(明明求得出原函数啊，-ln|x|,一个分段函数，见1.8.5)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 性质题 | false |
例1.8.4
解析
- 估值定理和积分的保号性
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
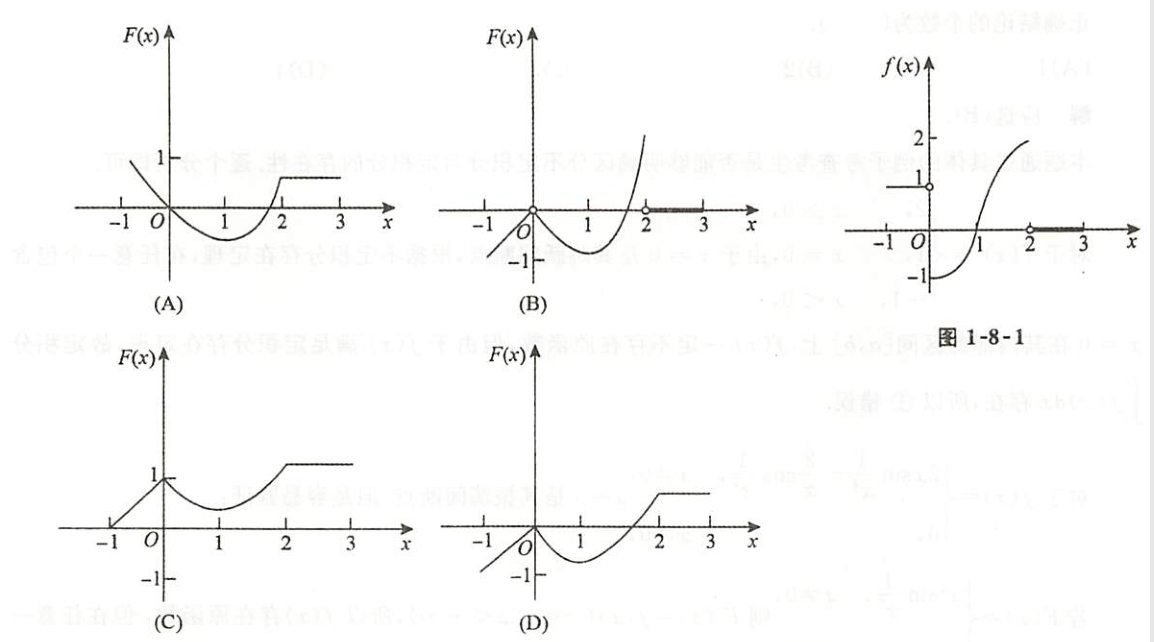
例1.8.5
解析
- 变限积分的不可导点，对应f(x)的间断点
- F(0)=0
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 超越理解范围 | false |
例题1.8.6
证明连续奇函数的一切原函数都是偶函数;连续偶函数的原函数中仅有一个原函数是奇函数
解析
- 注意：-x是怎么复合到变限积分函数中的
- 注意：还原法换的是积分元素
- 过程背下来
题型:
- 证明
错因:
教训:
(2020)子孙三代奇偶性
设奇函数$f(x)$在($-\infty,+\infty$)有连续导数,则
$\int_0^x[cosf(t)+f’(t)]dt$ 是____函数
解析
题型:
错因:
- 算出来内部是偶函数，忘记还套了一层变限积分，性质还要变一次
教训:
例题1.8.7
解析
- 华罗庚：数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休
- $\blacktriangleright$(？为什么积分上下限交换的话，互相为相反数)
题型:
错因:
教训:
例题1.8.8周期性
解析
- 2021预测题
- 如果原函数，积分函数都是以T为周期的函数，那么原函数在一个周期上的积分必然是0
- 若$f(x) \text{以T为周期}$且奇 $\implies \int_a^xf(t)dt \quad \text{以T为周期}$ 推导(02&t=00:53:31.454)
题型:
- 证明
错因:
教训:
例题1.8.9
解析
- 保号性
- 结论很重要
题型:
错因:
教训:
例1.8.10
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 超越理解范围 | false |
例1.8.11
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 忘记加常数C，公式背错，要加绝对值 | false |
例1.8.12
解析
- 第二换元积分法
- 三角代换
$\blacktriangleright$(为什么不能用cost代换)
- 必须选一个有反函数（sin单调，有反函数($(-\dfrac{\pi}{2},\dfrac{\pi}{2})$)
- 且取值能覆盖其取值范围的
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例1.8.13
解析
- 绝对值可以去掉的原因是$\sqrt{a^2+x^2}+x\text{永远}>0$
- 根据对数运算法则将a提出来
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 公式没记牢+小技巧 | false |
例1.8.14
解析
****
- 取一个取值范围内的函数
- $\blacktriangleright$(答案是不是有问题，倒数第2，3行)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例1.8.15
解析
- 法一：恒等变形、凑微分法,
- 法二: 恒等变形、凑微分法,换元法，有理函数积分
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例1.8.16
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例题1.8.17
解析
- 分部积分法，用表格法，轻轻松松
- $\mho$(分部积分法的适用范围)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 忘加常数C | true |
例1.8.18
解析
- 算出来的和答案不一样
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例1.8.19
解析
例1.8.20
解析
总结：有理函数一般会直接把根号代换
- 一共五种方法:(基本积分公式，凑微分法，换元法,分部积分，有理函数积分)
- 第一部只有可能是换元和有理函数积分
- 换元法，试了倒代换和三角代换都不行
- 估计是有理函数积分，但是有理函数积分并不熟悉，不知道怎么操作
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 | false |
例题1.8.21
解析
- 直接特殊值法解出来值
- 比较最高项系数
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 草稿打错 |
例1.8.22
解析
一看就是有理函数积分
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 配错系数 | false |
例题1.8.23
解析
- 夹逼失效
- 只能用定积分的定义
计算极限的题
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 |
例题1.8.24
解析
- 分子分母不是齐次的一般用夹逼
- 凑定积分的定义轻轻松松
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false | true |
例1.8.25
解析
- 定积分通过奇偶性省去一半的功夫
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例1.8.26
解析
- 轻轻松松(根代换)
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 系数配错 | false |
例1.8.27
解析
$tanx =t$
- 别样的三角代换，tan代换-$cos^2$
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 | false |
例1.8.28
解析
- 差最后一步根号代换
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例题1.8.29
解析
- 区间再现公式的证明
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 | true |
例题1.8.30
解析
- 华里士公式的应用sin(0-$\pi$)的公式
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例1.8.31
解析
- 这也太能凑了，
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 | false |
例题1.8.32
解析
- 区间再现换元法
- 三角有理式的积分
- 还能将两项加起来
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 | true |
例题1.8.33
解析
- 华里士公式的证明
- 只会考结论，不会考证明
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| true |
例1.8.34
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例1.8.35
解析
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| false |
例1.8.36
解析
- 先配方，再代换
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|---|---|---|
| 思路 | false |
例题1.10.5
解析
- $\flat$ 重要题源
题型:
错因:
教训:
(2020)
解析
- 点火公式