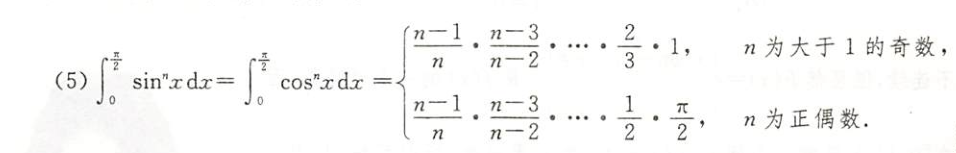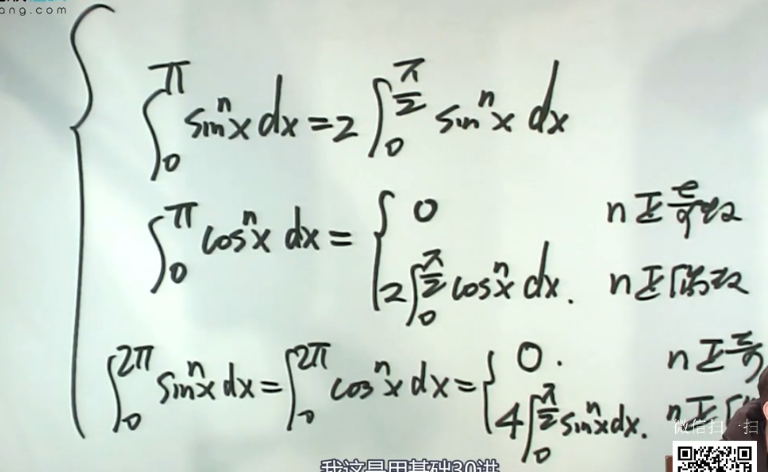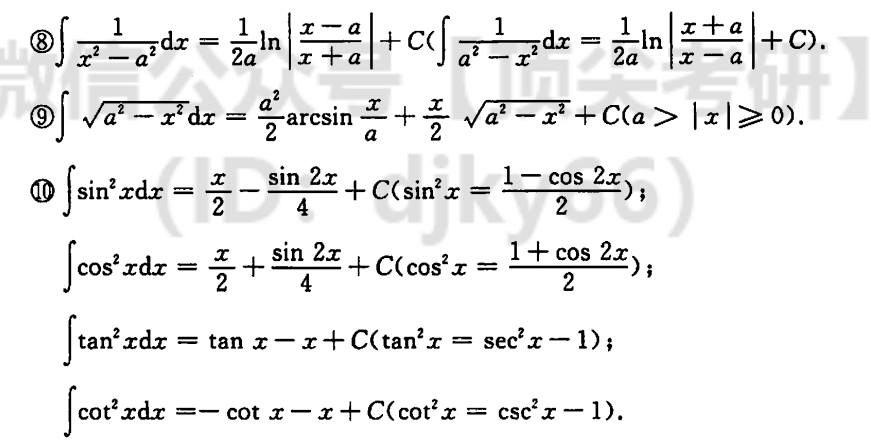zy2022
高等数学
基本积分表
| 公式 | 题目 |
|---|---|
| $\int x^kdx=\dfrac{1}{k+1}x^{k+1}+C,k\neq-1$ | |
| $\int \dfrac{1}{x^2}dx=-\dfrac{1}{x}+C$ | |
| $\int \dfrac{1}{\sqrt{x}}dx=2\sqrt{x}+C$ | |
| $\int \dfrac{1}{x}dx=ln\lvert x\rvert+C$ | |
| $\int e^xdx=e^x+C$ | |
| $\int a^xdx=\dfrac{a^x}{ln a}+C,(a >0 \text{且} a \neq 1)$ | |
| $\int e^xdx=e^x+C$ | |
| $\int sinxdx=-cosx+C$ | |
| $\int cos xdx=sin x+C$ | |
| $\int tan xdx=-ln\lvert cos x \rvert+C$ | |
| $\int cot xdx=ln\lvert sin x \rvert+C$ | |
| $\int\dfrac{dx}{cosx}=\int secxdx=ln\lvert secx+tanx \rvert+C$ | 1 |
| $\int\dfrac{dx}{sinx}=\int cscxdx=ln\lvert cscx-cotx \rvert+C$ | |
| $\int sec^2xdx=tanx+C$ | |
| $\int csc^2xdx=-cotx+C$ | |
| $\int secxtanxdx=secx+C$ | |
| $\int cscxcotxdx=-cscx+C$ | |
| $\int \dfrac{1}{1+x^2}dx=arctanx+C$ | |
| $\int \dfrac{1}{a^2+x^2}dx=\dfrac{1}{a}arctan\dfrac{x}{a}+C$ | |
| $\int\dfrac{1}{\sqrt{1-x^2}}dx=arcsinx+C$ | |
| $\int\dfrac{1}{\sqrt{a^2-x^2}}dx=arcsin\dfrac{x}{a}+C$ | |
| $\int\dfrac{1}{\sqrt{x^2+a^2}}dx=ln(x+\sqrt{x^2+a^2})+C(\text{常见}a=1)$ | |
| $\int\dfrac{1}{\sqrt{x^2-a^2}}dx=ln\lvert x+\sqrt{x^2-a^2} \rvert+C(\lvert x\rvert>\lvert a \rvert)$ | |
| $\int\dfrac{1}{x^2-a^2}dx=\dfrac{1}{2a}ln\lvert \dfrac{x-a}{x+a} \rvert+C(\int \dfrac{1}{a^2-x^2}dx=\dfrac{1}{2a}ln \lvert \dfrac{x+a}{x-a} \rvert +C)$ | |
| $\int\sqrt{a^2-x^2}dx=\dfrac{a^2}{2}arcsin\dfrac{x}{a}+\dfrac{x}{2}\sqrt{a^2-x^2}+C$ | |
| $\int sin^2xdx=\dfrac{x}{2}-\dfrac{sin 2x}{4}+C(sin^2x=\dfrac{1-cos2x}{2})$ | |
| $\int cos^2xdx=\dfrac{x}{2}+\dfrac{sin 2x}{4}+C(cos^2x=\dfrac{1+cos2x}{2})$ | |
| $\int tan^2xdx=tanx-x+C(tan^2x=sec^2x-1)$ | |
| $\int cot^2xdx=-cotx-x+C(cot^2x=csc^2x-1)$ |
华里士公式(点火公式)