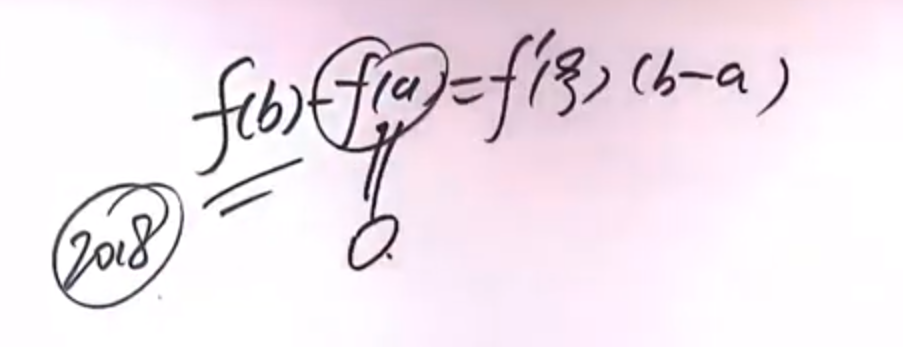凑数

例题1：

设$f(x)=x^2,f(\varphi(x))=-x^2+2x+3$,且$\varphi(x) \geq 0$,求$\varphi(x)$及其定义域与值域

解析
- 变量广义化
- 一致单调性
值域的解法
- 画图
- 配方
- 求导

例题2：

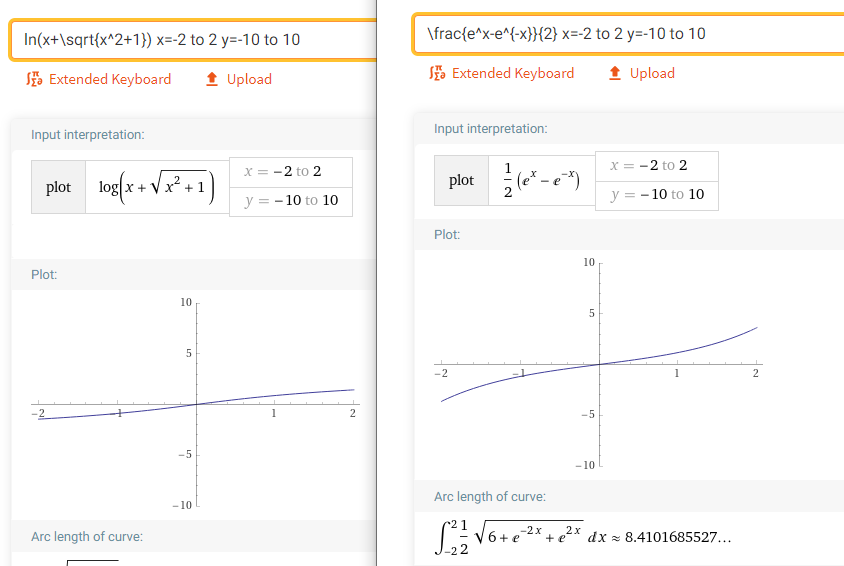
求函数$y=f(x)=ln(x+\sqrt{x^2+1})$的反函数$f^{-1}(x)$的表达式及其定义域

拓展
- $\int_{-1}^{1}[ln(x+\sqrt{x^2+1})+x^2]dx=$
  - 奇函数前面直接等于0，所以只用积后面的分

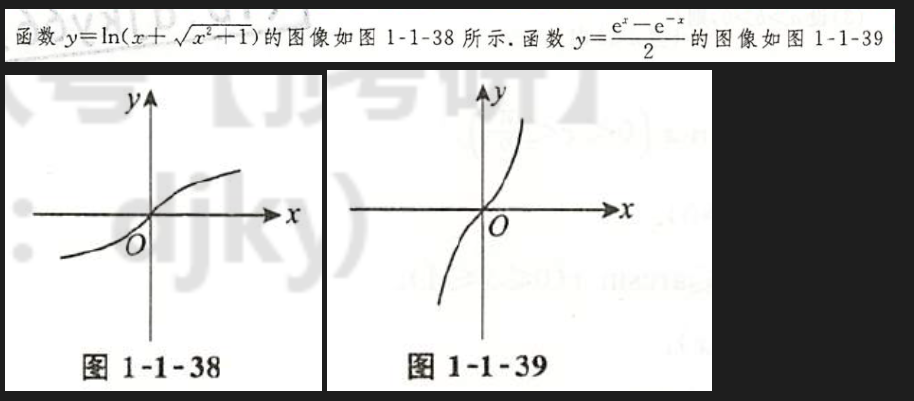
两个函数图像和都是奇函数要记住

$y=ln(x+\sqrt{x^2+1})$
- $sinh^{-1}(x)$
- 由于$x+|x|>0$,所以函数$- \infty\leq x \leq + \infty$处处有定义
- 奇函数推导（运用分子有理化公式$\sqrt{a}-\sqrt{b}=\dfrac{a-b}{\sqrt{a}+\sqrt{b}}$）
  - $f(-x)=ln(-x+\sqrt{x^2+1})=\dfrac{1}{ln(x+\sqrt{x^2+1})}=-ln(x+\sqrt{x^2+1})=-f(-x)$
- 单调性求导$(ln(x+\sqrt{x^2+1})’=\dfrac{1}{\sqrt{x^2+1}})$(基本求导公式p60)(基本积分表p110)
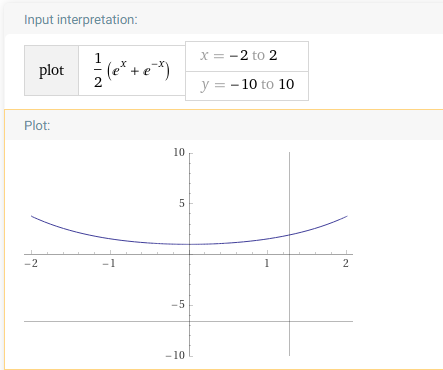
$y=\dfrac{e^x-e^{-x}}{2}$
- $sinh(x)$：双曲正弦
- f(x)-f(-x)直接就是奇函数
  - 其实可以现场按照定义推
- 悬链线

为什么我用wolframe画出来的和书本上不一样

例题3

将下列各组函数$f(x)$与$\varphi(x)$复合，求复合函数$f[\varphi(x)]$

$$
f(x) = \begin{cases}
2-x \text{, }& x \leq 0 \
x+2 \text{, }& x > 0
\end{cases}
\qquad
\varphi(x) = \begin{cases}
x^2 \text{, }& x < 0 \
-x \text{, }& x \geq 0
\end{cases}
$$

$$
f(x) = \varphi(x) = \begin{cases}
x \text{, }& x \geq 0 \
\dfrac{1}{x} \text{, }& x < 0
\end{cases}
$$

步骤解析

先广义化
画图
直接写答案

$\blacktriangleright$ 我认为广义化之后直接列方程即可,虽然我之前也是画图，但是好像没有那么清晰，复杂的话，图都不好画

$\bigstar$ 练习：习题1.1.1

设
$$
f(x) = \begin{cases}
ln\sqrt{x} \text{, }& x \geq 1 \
2x-1 \text{, }& x < 1
\end{cases}
$$
求$f[f(x)]$

解题思路
- 画图：$ln\sqrt{x}=\dfrac{1}{2}ln(x)$ $\spadesuit$(p20:对数运算法则)，$\spadesuit$(p13:伸缩变换)
  - $ln\sqrt{x}=\dfrac{1}{2}ln(x)$
  - $ln(\dfrac{1}{x})=-ln(x)$
  - $ln(1+\dfrac{1}{x})=ln(1+x)-ln(x)$(f(b)-f(a)拉格朗日中值定理)

证明函数$f(x)=\dfrac{x}{1+x^2}在(-\infty,+\infty)$内有界

解析

证明有界性的武器：不等式，极限，单调性

几何平均值小于算数平均值
$|f(x)|<M$
用极限的存在性来证明有界性
没有极限就用不等式
- ${\textstyle\unicode{x2460}}$ 当$x=0$时， $f(x)=0$(注意要讨论x=0的情况，因为除以0没有意义？)
- 当$x \neq 0$时，$f(x)=\dfrac{1}{\dfrac{1}{x}+x}$
- $|f(x)|=\dfrac{1}{\dfrac{1}{|x|}+|x|}$

证明过程:

$\text{当}x \neq 0时，|f(x)| = \dfrac{|x|}{1+x^2} = \dfrac{1}{\dfrac{1}{|x|}+|x|},$

$\text{由不等式} \dfrac{a+b}{2} \geq \sqrt{ab}(a,b>0),\text{有}\dfrac{1}{|x|}+|x| \geq 2\sqrt{\dfrac{1}{|x|}|x|}=2,\text{即}|f(x)|\leq \dfrac{1}{2}$

$\text{当}x=0时,f(0)=0.\text{综上，函数}f(x)\text{在}(-\infty,+\infty)\text{内有界}$

题型: 证明题

错因: 知识结构不清

教训

记得讨论0点
证明有界性的武器：不等式，极限，单调性

奇偶性：$\sharp$ 神秘的数字0和1

$\bigstar$(考研真题) 拉格朗日缺0（加减法）
缺1(乘除法)
- $f(x)>xf(1)$
- $\dfrac{f(x)}{x}>\dfrac{f(1)}{1}$
- 令$F(x)=\dfrac{f(x)}{x}$

有界性的证明

$|f(x)|<M$
用极限的存在性来证明有界性
没有极限就用不等式
- ${\textstyle\unicode{x2460}}$ 当$x=0$时， $f(x)=0$
- 当$x \neq 0$时，$f(x)=\dfrac{1}{\dfrac{1}{x}+x}$
- $|f(x)|=\dfrac{1}{\dfrac{1}{|x|}+|x|}$
用不等式证明单调性
- 命题:$x_{n+1}=sinx_n<x_n \implies{x_n}$
$e^x \geq x+1$

ednow

考研数学题目-ch1

凑数

凑数

凑数

凑数