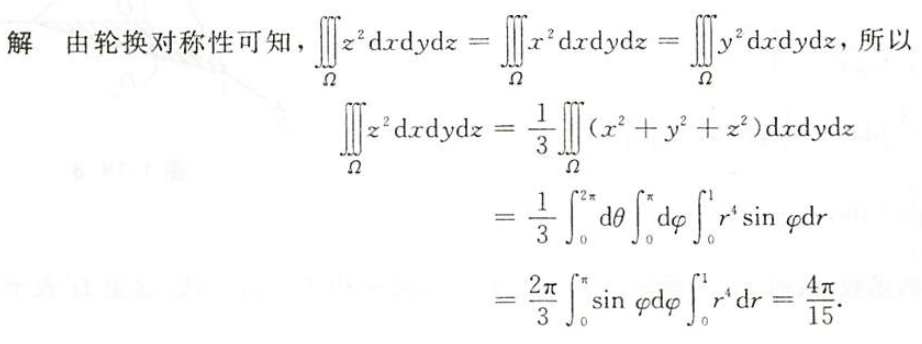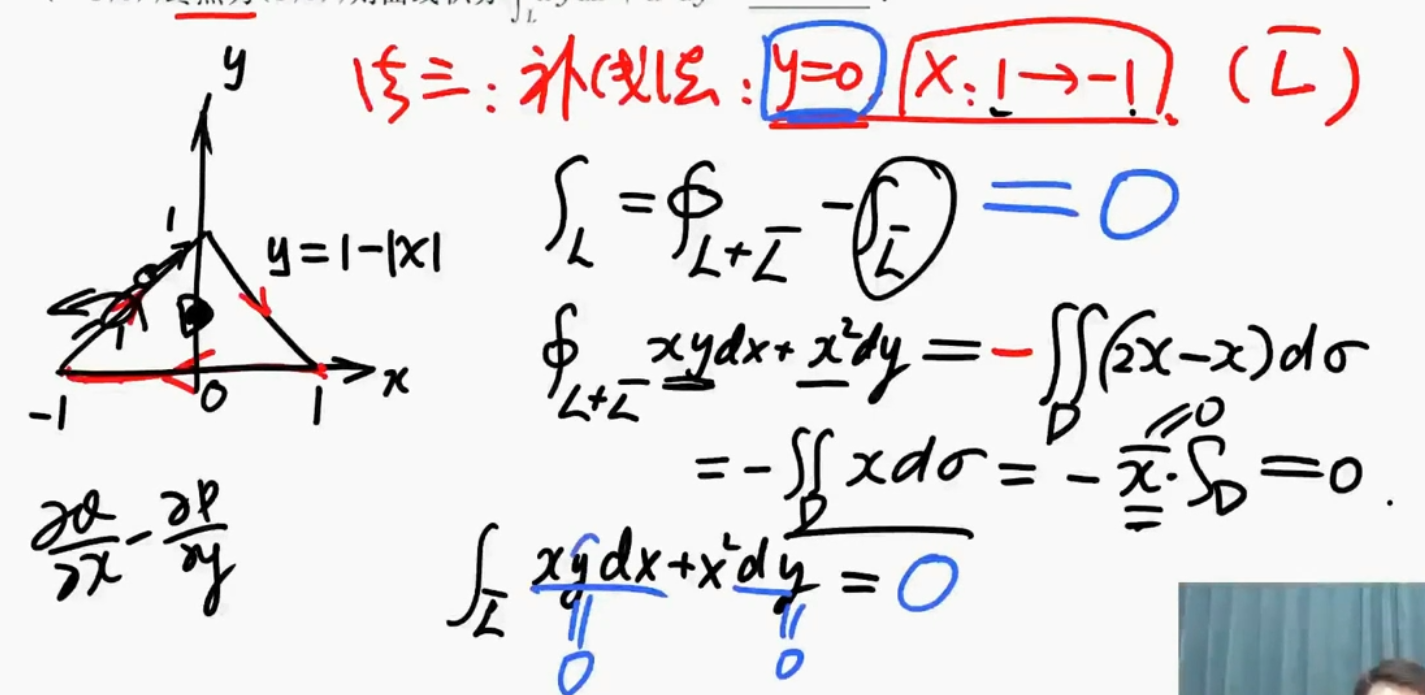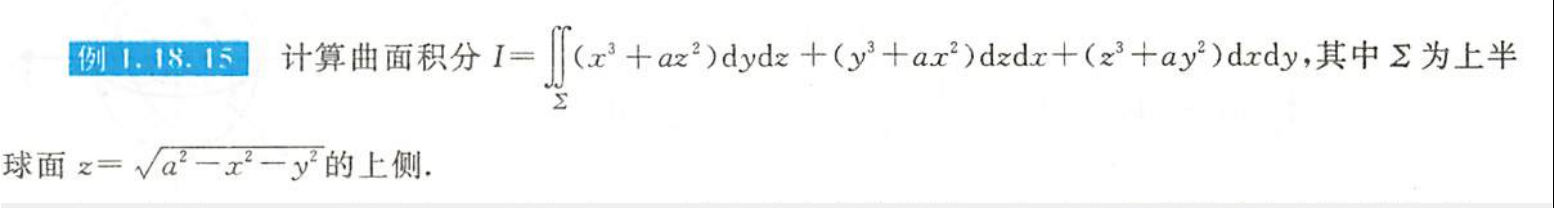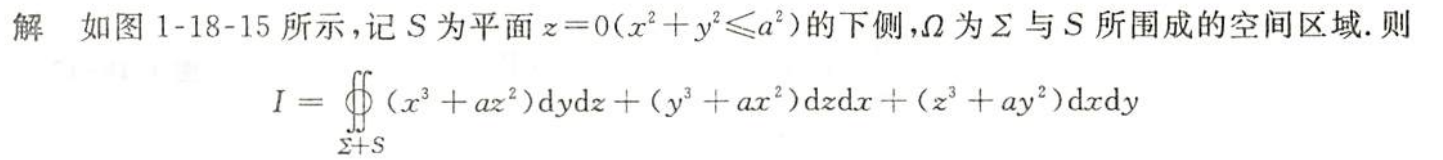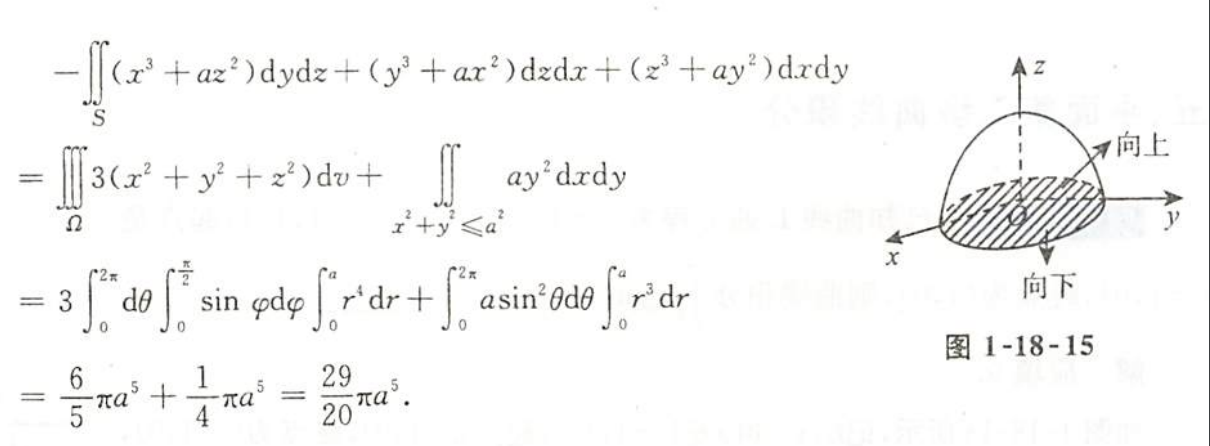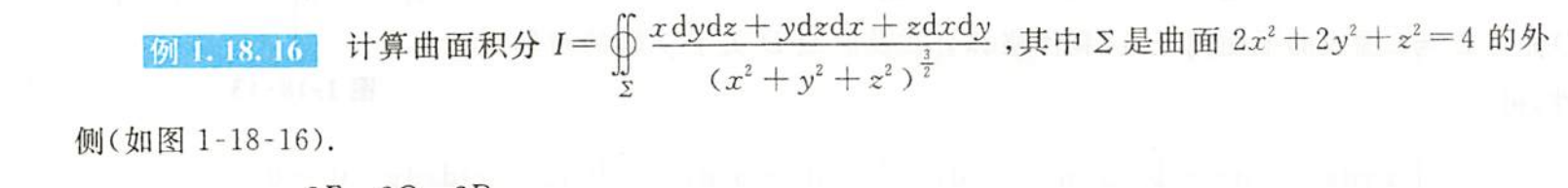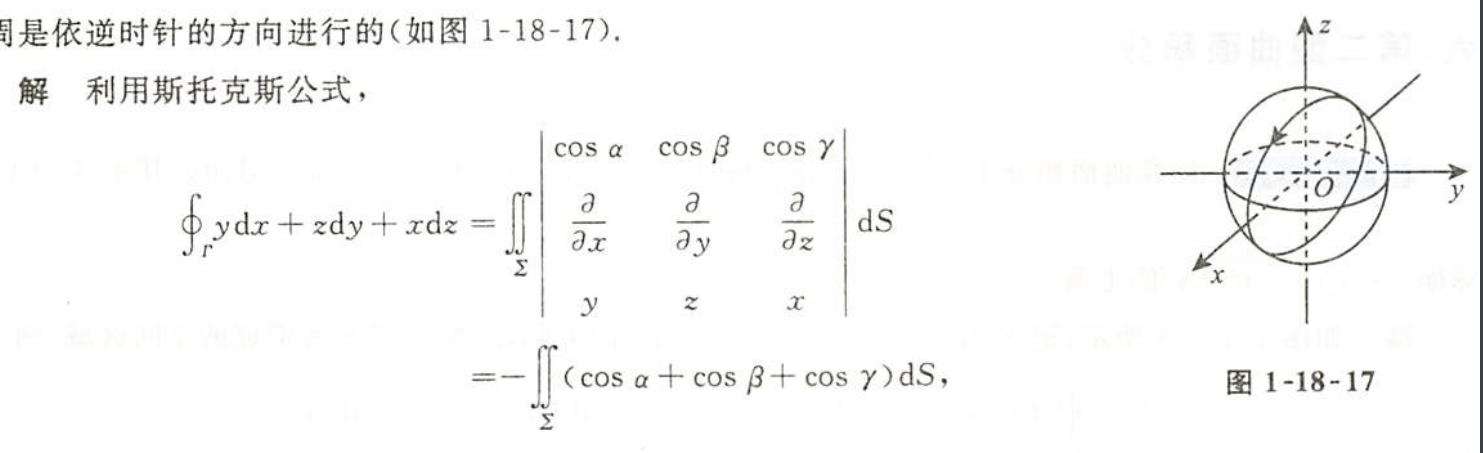zy2022
高等数学
凑数
ch1.高等数学预备知识
例题1:
设$f(x)=x^2,f(\varphi(x))=-x^2+2x+3$,且$\varphi(x) \geq 0$,求$\varphi(x)$及其定义域与值域
例题2:
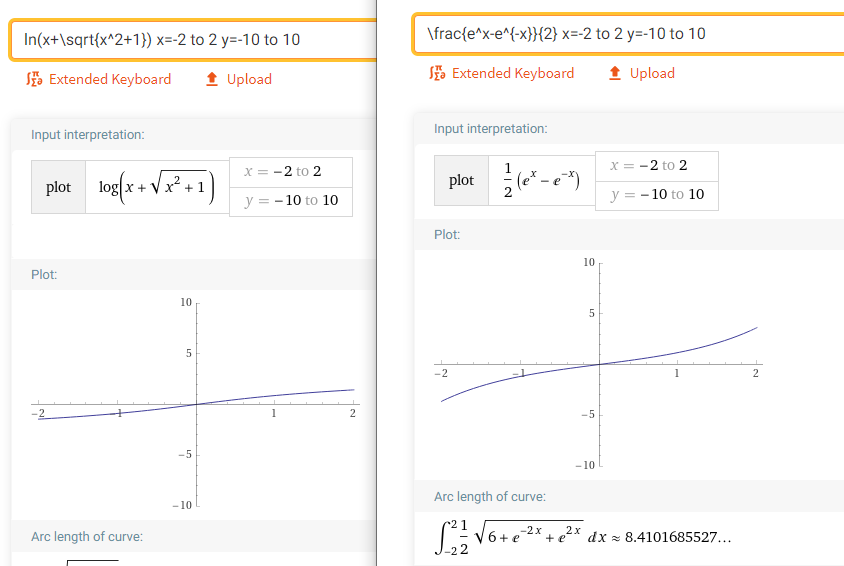
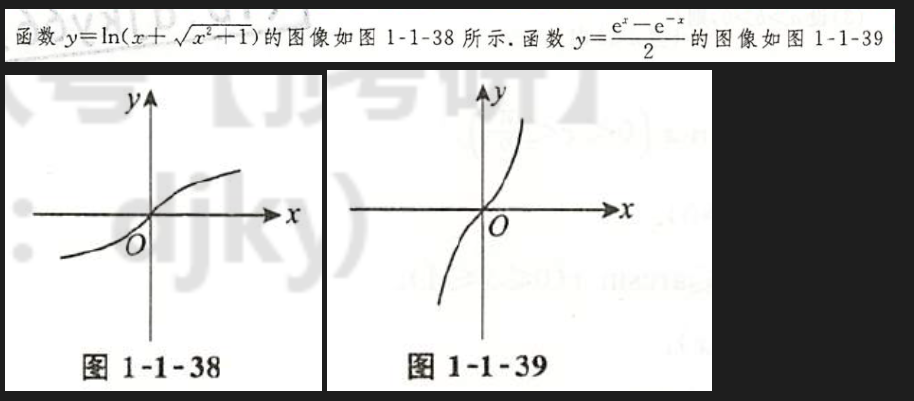
求函数$y=f(x)=ln(x+\sqrt{x^2+1})$的反函数$f^{-1}(x)$的表达式及其定义域
- 拓展
- $\int_{-1}^{1}[ln(x+\sqrt{x^2+1})+x^2]dx=$
两个函数图像和都是奇函数要记住

为什么我用wolframe画出来的和书本上不一样

例题3
将下列各组函数$f(x)$与$\varphi(x)$复合,求复合函数$f[\varphi(x)]$
$$
f(x) = \begin{cases}
2-x \text{, }& x \leq 0 \
x+2 \text{, }& x > 0
\end{cases}
\qquad
\varphi(x) = \begin{cases}
x^2 \text{, }& x < 0 \
-x \text{, }& x \geq 0
\end{cases}
$$
$$
f(x) = \varphi(x) = \begin{cases}
x \text{, }& x \geq 0 \
\dfrac{1}{x} \text{, }& x < 0
\end{cases}
$$
步骤解析
- 先广义化
- 画图
- 直接写答案
$\blacktriangleright$ 我认为广义化之后直接列方程即可,虽然我之前也是画图,但是好像没有那么清晰,复杂的话,图都不好画
$\bigstar$ 练习:习题1.1.1
设
$$
f(x) = \begin{cases}
ln\sqrt{x} \text{, }& x \geq 1 \
2x-1 \text{, }& x < 1
\end{cases}
$$
求$f[f(x)]$
- 解题思路
- 画图:$ln\sqrt{x}=\dfrac{1}{2}ln(x)$ $\spadesuit$(p20:对数运算法则),$\spadesuit$(p13:伸缩变换)
- $ln\sqrt{x}=\dfrac{1}{2}ln(x)$
- $ln(\dfrac{1}{x})=-ln(x)$
- $ln(1+\dfrac{1}{x})=ln(1+x)-ln(x)$(f(b)-f(a)拉格朗日中值定理)
证明函数$f(x)=\dfrac{x}{1+x^2}在(-\infty,+\infty)$内有界
解析
证明有界性的武器:不等式,极限,单调性
- 几何平均值小于算数平均值
- $|f(x)|<M$
- 用极限的存在性来证明有界性
- 没有极限就用不等式
- ${\textstyle\unicode{x2460}}$ 当$x=0$时, $f(x)=0$(注意要讨论x=0的情况,因为除以0没有意义?)
- 当$x \neq 0$时,$f(x)=\dfrac{1}{\dfrac{1}{x}+x}$
- $|f(x)|=\dfrac{1}{\dfrac{1}{|x|}+|x|}$
证明过程:
$\text{当}x \neq 0时,|f(x)| = \dfrac{|x|}{1+x^2} = \dfrac{1}{\dfrac{1}{|x|}+|x|},$
$\text{由不等式} \dfrac{a+b}{2} \geq \sqrt{ab}(a,b>0),\text{有}\dfrac{1}{|x|}+|x| \geq 2\sqrt{\dfrac{1}{|x|}|x|}=2,\text{即}|f(x)|\leq \dfrac{1}{2}$
$\text{当}x=0时,f(0)=0.\text{综上,函数}f(x)\text{在}(-\infty,+\infty)\text{内有界}$
题型: 证明题
错因: 知识结构不清
教训
- 记得讨论0点
- 证明有界性的武器:不等式,极限,单调性
奇偶性:$\sharp$ 神秘的数字0和1
- $\bigstar$(考研真题) 拉格朗日缺0(加减法)
- 缺1(乘除法)
- $f(x)>xf(1)$
- $\dfrac{f(x)}{x}>\dfrac{f(1)}{1}$
- 令$F(x)=\dfrac{f(x)}{x}$
有界性的证明
- $|f(x)|<M$
- 用极限的存在性来证明有界性
- 没有极限就用不等式
- ${\textstyle\unicode{x2460}}$ 当$x=0$时, $f(x)=0$
- 当$x \neq 0$时,$f(x)=\dfrac{1}{\dfrac{1}{x}+x}$
- $|f(x)|=\dfrac{1}{\dfrac{1}{|x|}+|x|}$
- 用不等式证明单调性
- 命题:$x_{n+1}=sinx_n<x_n \implies{x_n}$
- $e^x \geq x+1$
ch2.数列极限
题数总结
例1.2.3
解析
总结
例1.2.4
解析
总结
例1.2.6

解析
总结
例1.2.7

解析
总结
ch3.函数极限
题数总结
p47
例1.3.1

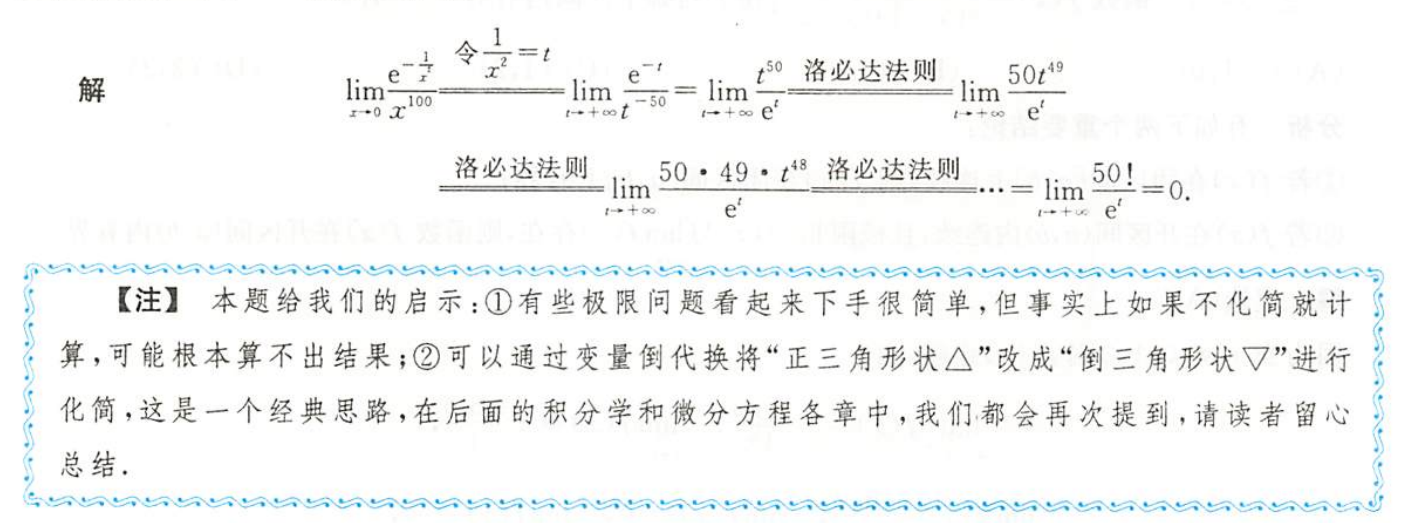
解析

总结
($\bigstar$ 真题)例1.3.2

解析

总结
例1.3.3

解析

总结
例1.3.4

解析

- 七种未定式中的0比0
- 见根号差,用有理化
- 洛必达,等价无穷小的比
总结
例1.3.5

解析

总结
例1.3.6

解析

总结
例1.3.7

注意这道题是$ln x \cdot ln (1-x)$
解析

总结
例1.3.8

解析

总结
例1.3.9

解析

总结
例1.3.10

解析

- 七种未定式中的无穷减无穷
- 中间用等价无穷小是不是太牵强附会了
总结
例1.3.11

解析

总结
例1.3.12

解析

总结
例1.3.13

解析

总结
例1.3.14

解析

总结
例1.3.15

解析

- 分子分母同乘x
- 配一个极限为0
- 我取巧,直接让洛必达可洛来做
总结
例1.3.16

解析

总结
例1.3.17

解析

总结
例1.3.18

解析

总结
例1.3.19

解析

总结
例1.3.20

解析

总结
例1.3.21

解析

总结
例1.3.22

解析
总结
例1.3.23

解析

总结
例1.3.24

解析

总结
ch8.一元函数积分学的概念与计算
注
[1.8.6,1.8.9]都没做,都是证明题,之后重新回来再做先做计算题
本节例题49道,课后题21道,300题14道,一共84道题
尚有题未总结
解析
总结
变限积分求导时x出现在被积函数中

解析

总结
上限无穷大的变限积分收敛不代表原函数趋于无穷的极限为0
解析

总结
例题1.8.1

解析

- 积分中值定理
- $\blacktriangleright$(本来积分中值定理就是闭区间,他怎么变成开区间了,感觉步骤有问题,教材怎么写的)
- 凑导数的定义$\displaystyle \lim_{\Delta x\to 0}\dfrac{\Delta F}{\Delta x}$
思路:
联系 F(x) 和 F$\prime$(x)的方法:积分中值定理
积分可拆性凑出积分中值定理,用定义约掉$\Delta x$
出现F$\prime \prime$(x)的方法,三次罗尔中值定理,两次拉格朗日中值定理,泰勒展开到二阶
题型: 证明题
错因: 超越理解范围
教训:
上课的时候应该把思路记下来
例题1.8.2

解析


思路
肯定是反证法
导数的定义+洛必达
题型:
错因:
教训:
例1.8.3

解析

$\blacktriangleright$(明明求得出原函数啊,-ln|x|,一个分段函数,见1.8.5)
总结
例1.8.4

解析

总结
例1.8.5


解析

- 变限积分的不可导点,对应f(x)的间断点
- F(0)=0
总结
例题1.8.6
证明连续奇函数的一切原函数都是偶函数;连续偶函数的原函数中仅有一个原函数是奇函数
解析
- 注意:-x是怎么复合到变限积分函数中的
- 注意:还原法换的是积分元素
- 过程背下来
题型:
错因:
教训:
(2020)子孙三代奇偶性
设奇函数$f(x)$在($-\infty,+\infty$)有连续导数,则
$\int_0^x[cosf(t)+f’(t)]dt$ 是____函数
解析
题型:
错因:
- 算出来内部是偶函数,忘记还套了一层变限积分,性质还要变一次
教训:
例题1.8.7
解析
- 华罗庚:数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休
- $\blacktriangleright$(?为什么积分上下限交换的话,互相为相反数)
题型:
错因:
教训:
例题1.8.8周期性
解析
- 2021预测题
- 如果原函数,积分函数都是以T为周期的函数,那么原函数在一个周期上的积分必然是0
- 若$f(x) \text{以T为周期}$且奇 $\implies \int_a^xf(t)dt \quad \text{以T为周期}$ 推导(02&t=00:53:31.454)
题型:
错因:
教训:
例题1.8.9
解析
题型:
错因:
教训:
例1.8.10

解析

总结
例1.8.11

解析

总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|
| 忘记加常数C,公式背错,要加绝对值 | | false |
例1.8.12
解析
$\blacktriangleright$(为什么不能用cost代换)
- 必须选一个有反函数(sin单调,有反函数($(-\dfrac{\pi}{2},\dfrac{\pi}{2})$)
- 且取值能覆盖其取值范围的
总结
例1.8.13

解析


- 绝对值可以去掉的原因是$\sqrt{a^2+x^2}+x\text{永远}>0$
- 根据对数运算法则将a提出来
总结
例1.8.14

解析
 ****
****
- 取一个取值范围内的函数
- $\blacktriangleright$(答案是不是有问题,倒数第2,3行)
总结
例1.8.15

解析

- 法一:恒等变形、凑微分法,
- 法二: 恒等变形、凑微分法,换元法,有理函数积分
总结
例1.8.16

解析


总结
例题1.8.17

解析
- 分部积分法,用表格法,轻轻松松
- $\mho$(分部积分法的适用范围)
总结
例1.8.18

解析
总结
例1.8.19

解析


- 法二分部积分表格不再适用,他在分部积分的时候还用了凑微分、
- 用持续用分部积分表格将卡在这步

总结
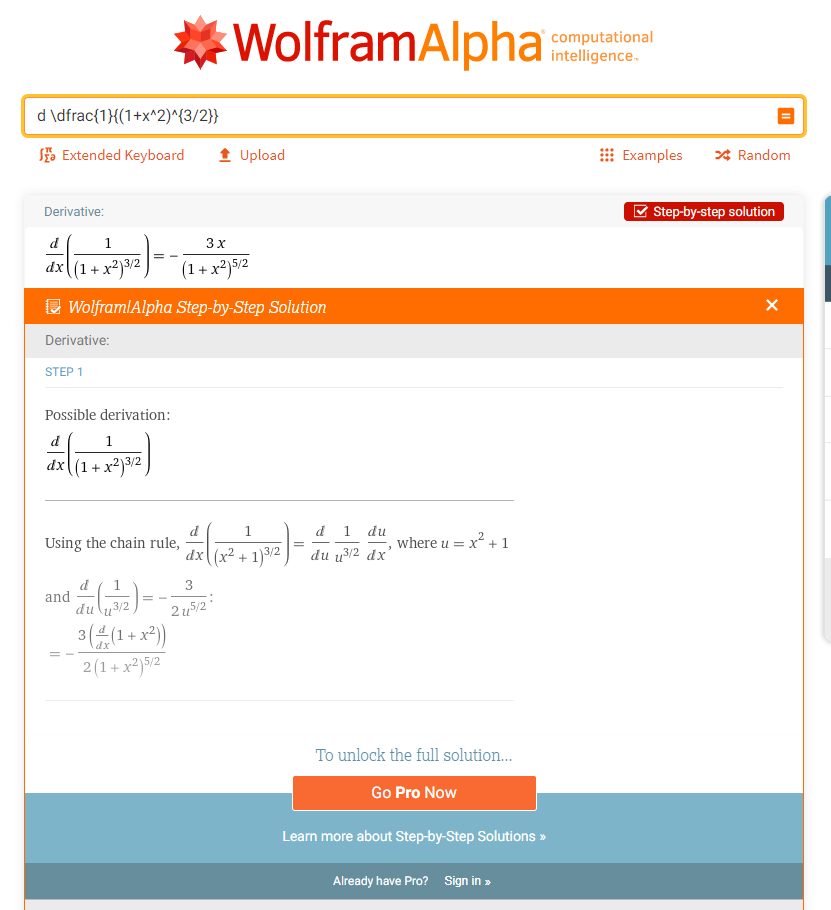
例1.8.20

解析

总结:有理函数一般会直接把根号代换
- 一共五种方法:(基本积分公式,凑微分法,换元法,分部积分,有理函数积分)
- 第一部只有可能是换元和有理函数积分
- 换元法,试了倒代换和三角代换都不行
- 估计是有理函数积分,但是有理函数积分并不熟悉,不知道怎么操作
总结
例题1.8.21

解析


总结
例1.8.22

解析
一看就是有理函数积分
总结
例题1.8.23

解析

计算极限的题
总结
例题1.8.24

解析

- 分子分母不是齐次的一般用夹逼
- 凑定积分的定义轻轻松松
总结
例1.8.25

解析

总结
例1.8.26

解析

总结
例1.8.27

解析

$tanx =t$
总结
例1.8.28

解析

总结
例题1.8.29

解析

总结
例题1.8.30

解析

总结
例1.8.31

解析

总结
例题1.8.32

解析


总结
例题1.8.33

解析

总结
例1.8.34

解析

总结
例1.8.35

解析

总结
例1.8.36

解析


总结
例题1.10.5
解析
题型:
错因:
教训:
(2020)
解析

题型:
错因:
教训:
ch9.一元函数积分学的几何应用
例题1.9.1
直角坐标系下的面积
解析
总结
例题1.9.2
解析
- $\bigstar$
- 参数方程
- 平摆线:车轱辘的车轮的一点的轨迹
- $\flat$ 困难的年份都是大题
- 第二个直接奇偶性,$cos^2x$直接点火公式
总结
例题1.9.3
解析
总结
例1.9.8
解析
总结
(2019)

解析
总结
ch10.积分等式与积分不等式
例1.10.1
解析
- 推广的中值定理
- 积分中值定理是其一个特例
- 柯西中值定理快速证
总结
例1.10.3
解析
总结
例题1.10.4
解析
总结
例题1.10.6
解析
总结
习题1.10.3
解析
- 神秘的数字0和1,除过去比
- 0-x的平均值
- 积分中值定理,直接把积分变成原函数(儿子)
- $\bigstar$(题源)
总结
例题1.10.8
解析
- 用两次拉格朗日中值定理
- 算数平均值<平方平均值
- $\bigstar$
总结
例题1.10.10
解析
- $\bigstar$(题源) 积分法题源
- 分部积分的表格
- 反对幂指三知道具体函数才知道怎么求导,抽象函数看线索
总结
ch11.多元函数微分学
例1.11.2
解析
总结
例题1.11.7
解析
总结
习题1.11.8
解析
总结
例题1.11.3
解析
- 数学的习惯是表达成u,v但是考研的习惯一般是1,2
- 如果具有二阶连续偏导数,那么交换求偏导次序并不影响
总结
例题1.11.10
解析
总结
习题1.11.7
解析
总结
习题1.11.8
解析
- 本节的逆问题
- 注意加的不是常数C是$\varphi(y)$
- 小4分的题(必考题)
总结
ch12.二重积分
二重积分题目说明
例题1.12.1

解析

总结
例1.12.2

解析

总结
例题1.12.3

解析

- 普通对称性
- $\bigstar$(麻雀虽小五章俱全)
- 能拆则拆
- 直角坐标系上的积分
总结
| 题型 | 错因 | 教训 | 视频讲解 |
|---|
| 没有考虑被积函数的正负 | | true |
例1.12.4

解析

思路很清晰,一定是分情况讨论
总结
例题1.12.5

解析

总结
例1.12.6

解析


- 极坐标系换成直角坐标系
- $\blacktriangleright$(题目出错了?) x\text{应该小于}cos \theta$,没错,导数刚好就是阴影部分
- 二重积分别样的凑微分法
总结
例题1.12.7

解析

- $\flat$
- 命题老师往往会帮倒忙,他写成dxdy可能要转换为rdr
- 用$\text{积分下限}1-x \implies x+y=1 \implies rcos\theta + rsin\theta=1$
总结
例题1.12.8

解析
- $\bigstar$
- 常见:有原函数但求不出初等函数形式的原函数
- $\int \dfrac{sinx}{x}dx,\int \dfrac{cosx}{x}dx,\int \dfrac{tan x}{x}dx,\int \dfrac{e^x}{x}dx,sin\dfrac{1}{x},cos\dfrac{1}{x}$
- $\int sin x^2 dx,\int cos x^2 dx,\int tan x^2 dx,$
- $\int e^{ax^2+bx+c}dx (\int e^{x^2} dx,\int e^{-x^2} dx,)$
- $\int \dfrac{dx}{lnx}dx$
- 椭圆函数
- 交换积分次序
- 注意还要配方
- 注意正负,最好让所有的元素都出现在表格中操作
总结
例1.12.9

解析

- $\bigstar$ $\bigstar$ $\bigstar$
- 化一元积分为二重积分,交换积分次序
总结
例1.12.10

解析
总结
例1.12.11

解析

- $\bigstar$ 结果也很重要
- 广义的圆
- 高斯曲线的积分值为$\dfrac{\sqrt{\pi}}{2}$

总结
ch13.常微分方程
例1.13.1
解析
- 变量可分离型
- 写成$\dfrac{dy}{dx}=f(x)g(y)$
- 本来y不能为0,因为y被除到了分母上,所以c不能为0,但是y=0带进去是成立所以c为任意常数
- 丢失的解叫奇解
- 补奇解回来和通解组成全部解
- 考研数学只要求求通解
总结
例1.13.2
解析
- 可化为变量可分离型
- 正三角形的积分上下同乘,变成到倒三角的方便处理
总结
例题1.13.3
解析
总结
习题1.13.3
解析
- $\bigstar$ $\bigstar$ $\bigstar$
- 变成一阶线性微分方程

- $\mho$(分部积分的表格,谁在上面,谁在下面)
总结
例题1.13.7
解析
总结
ch14.无穷级数
例1.14.2
解析
- 根据p级数的概念迅速证明
- 放缩之后无界根据必要条件,必然发散
- 证明发散就放小,证明收敛就放大
总结
例1.14.3
解析
- 调和级数(导数的平均值为另外一个人的倒数)
- 级数对不等式的要求比较高
- $x>ln(1+x)$
总结
例1.14.6
解析
- $\bigstar$(考研的味道)
- 用不等式解决问题
- 大的收敛小的必收敛
总结
例题1.14.4
解析
- 达朗贝尔判别法
- ${(1+\dfrac{1}{n})^n}$是单调增加趋向e
总结
例1.14.5
解析
- 柯西判别法
- sinx-x和幂值函数的处理
- 相当于$\dfrac{1}{n}$次方,约掉一个
总结
例1.14.7
解析
总结
例1.14.8
解析
- $\bigstar$(非常经典的例子)
- 莱布尼茨判别法
总结
例1.14.10
解析
总结
例题1.14.11
解析
- $\bigstar$(考研风格)
- 积累
- 做题当中积累和学习(很像写代码,再写代码中学习和积累)
总结
例题1.14.13
解析
总结
例1.14.14
解析
- $\bigstar$(热门考点)
- 麻雀虽小五张俱全的题
总结
例1.14.15
解析
- 经典的题目
- 需要转为定积分或者变上限积分没不然要确定常数C
- n在分母上,先导后积(视频的先导后积公式的推导也在这里)
- $S(x)=S(x_0)+\int_{x_0}^xS’(t)dt$
- $\blacktriangleright$(为什么只能限定|t|<1)
总结
例1.14.16
解析
总结
例1.14.17
解析
- $\bigstar$(奇数年的考题风格)
- 相当于$\dfrac{1}{1+t^2}$的原因要知道
总结
例1.14.18
解析
总结
ch15.数一专题内容(应用题)
例1.15.1
解析
总结
例题1.15.2
解析
总结
习题1.15.4
解析
总结
习题1.15.5
解析
总结
例1.15.6
解析
总结
例1.15.7
解析
总结
1.15.8
解析
总结
1.15.9
解析
总结
例1.15.11
解析
- 用牛顿定律的公式
- 用到了反对幂指三的表格
- 第二问的级数用公共知识很难求
总结
例1.15.14
解析
- 周期是2
- $\blacktriangleright$(这题目好突兀。。)
总结
ch17.多元函数积分学的基础知识
题目详情
例题9道,习题6道
例1.17.1

解析
一道题复习高中的向量运算

$\overrightarrow{a} \times \overrightarrow{c} \cdot \overrightarrow{c}=0:\overrightarrow{a}\text{和}\overrightarrow{c}\text{叉乘的结果,与其形成的平面的法线方向垂直},\overrightarrow{c}\text{在这个平面上,所以结果为0}$
$(\overrightarrow{a} \times \overrightarrow{b}\cdot \overrightarrow{c})=(\overrightarrow{b} \times \overrightarrow{c}\cdot \overrightarrow{a})$是一个公式,证明如下


向量的坐标运算
- 数量积($\overrightarrow{i}\cdot \overrightarrow{j}=\overrightarrow{i}\cdot \overrightarrow{k}=0$,$\overrightarrow{i}\cdot \overrightarrow{i}=1$)
- 数量积($\overrightarrow{i}\times \overrightarrow{i}=\overrightarrow{j}\times \overrightarrow{j}= \overrightarrow{k} \times \overrightarrow{k} =0$,$a\overrightarrow{i}\times b\overrightarrow{j}=ab \overrightarrow{k}$)

显然亦可用混合积的行列式推导得
总结
例1.17.2
解析
- $\bigstar$ 空间曲面的切平面与法线
- 这道题对发现的方向没有限制,都是一个平面
总结
例1.17.3

解析

- 在哪个面,就消去哪个元
- 舍去不需要的部分(?这个步骤怎么想到的)
- 加上取值范围
总结
例1.17.4

解析

- 旋转曲面的题目
- 技巧:绕着哪个轴转,对应的字母不变
- 强化班讲这个图怎么画
- 注意平方的存在
总结
例1.17.5

解析

总结
例1.17.6

解析

总结
例1.17.7

解析

总结
例1.17.8

解析

总结
例1.17.9

解析

- 旋度
- $\blacktriangleright$(忘了行列式的计算公式)
- 三阶行列式
总结
例1.18.3

解析
总结
例1.18.4
解析
总结
例1.18.17
解析
总结
习1.18.7
解析
总结
ch18.三重积分与曲线曲面积分
题数统计
例1.18.1

解析
- 三重积分的基本方法
- 先1后2法,投影穿线法
- 写的时候写上谁的上限和下限,看的比较清楚
为什么没有面积定理:算错了,其实不是常数,不然是有的
求导公式的逆用积分用错
计算能力不行
总结
例1.18.2

解析

- 普通对称性
- 关于y对称
- 先二后一法
- 因为z相当于常数提走了
- z不在二重积分里面,可以用二重积分的面积性质
总结
例1.18.3

解析

$\mho$(为什么我的方法不对??)

总结
例1.18.4

解析

总结
例1.18.5

解析

总结
例1.18.6
解析
总结
例1.18.7
解析
总结
例1.18.8
解析
- 考研真题
- 普通对称性加轮换对称性
- $\blacktriangleright$(为什么不是x写成y和z的函数)
总结
例1.18.9
解析
总结
例1.18.10
解析
- $\bigstar$ $\bigstar$ $\bigstar$
- 对于对应投影部分的面积可以用上一讲的投影知识,投到哪个面就保留对应的字母
总结
例1.18.11
解析
总结
例1.18.13
解析
- 三种解法
- 第二型曲线积分
- 由对称性很容易得到结果是0
- 还可以用格林公式
格林公式的解法

总结
例1.18.14

解析

- 挖洞法下去回来了,抵消
- 积分与路径无关
- 椭圆的面积
- 永远取分母=一个常数
- $\pi ab$
总结
例1.18.15

解析


- 补面法,高斯公式
- “上侧”证明指定的正方向是上面
- 没有分母一阶偏导数一定连续
如果不用高斯公式怎么做
总结
例1.18.16

解析

总结
例1.18.17

解析


- 斯托克斯,z分量是正数
- 斯托克斯会有二型面积积分的问题
由斯托克斯有求一个平面的法向量即可,这时候直接求题目给的$x+y+z=0$的法向量
$$F=x+y+z \implies \overrightarrow{n}={F’_x,F’_y,F’_z}={1,1,1},F’_z\text{的正负需要额外考虑}$$
我居然是想用高中知识求法向量
总结
习1.18.17
解析
- 斯托克斯,z分量是负数
- 斯托克斯会有二型面积积分的问题
总结

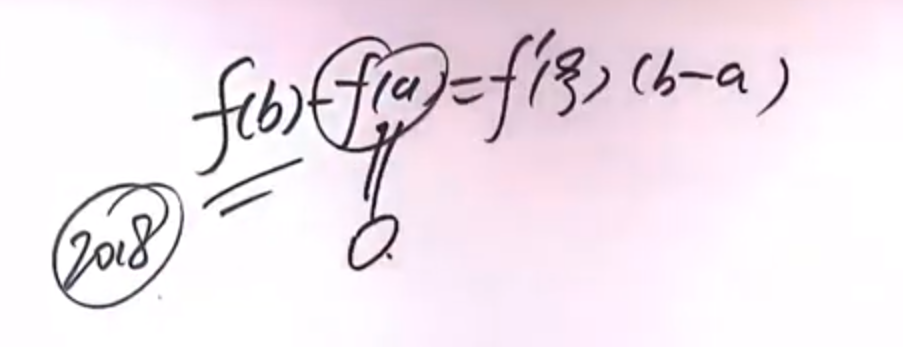
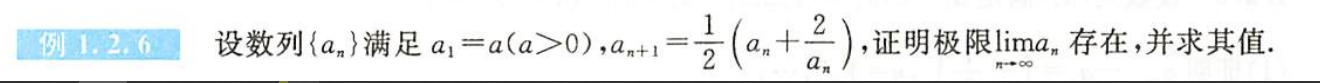
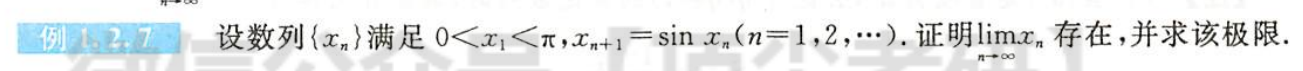
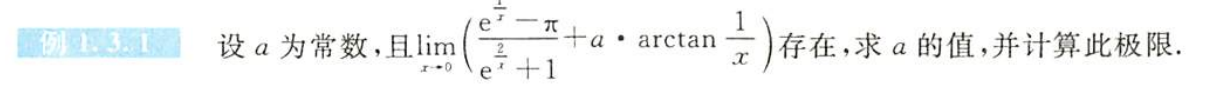




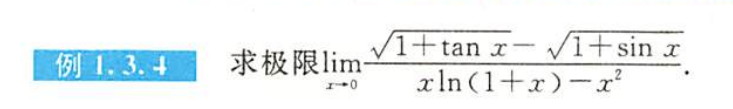

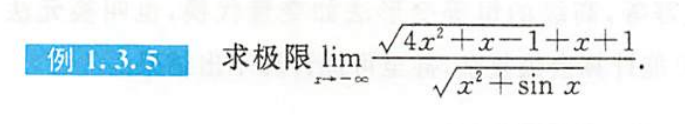

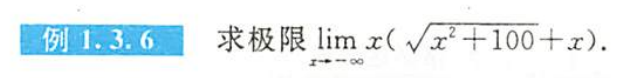


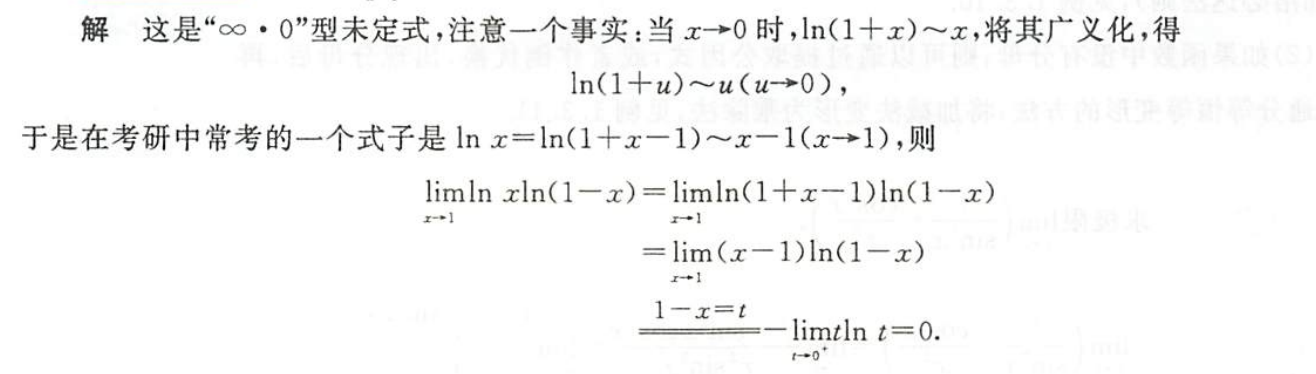
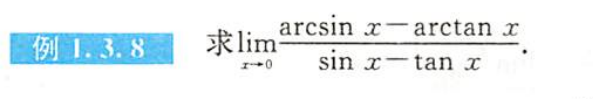

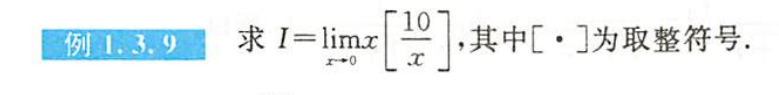

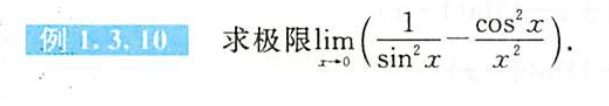
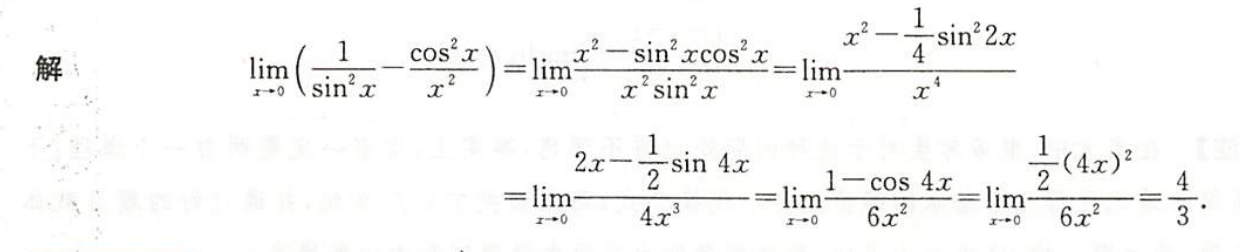

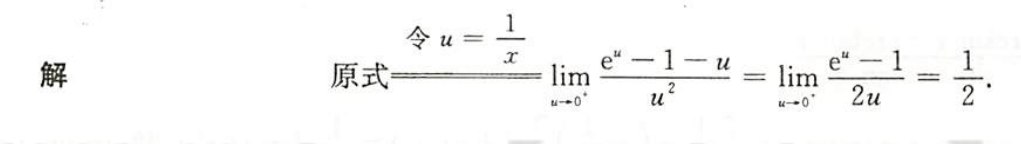
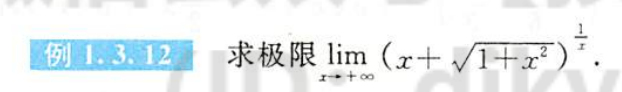



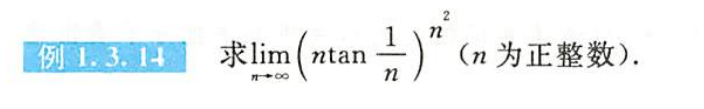
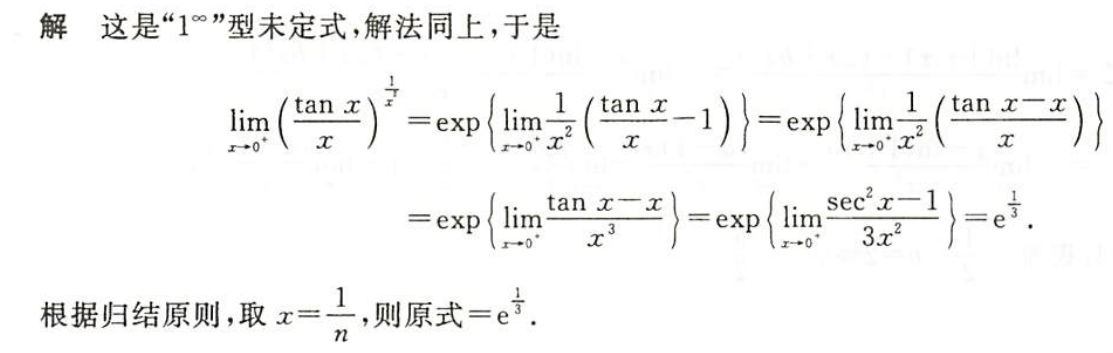


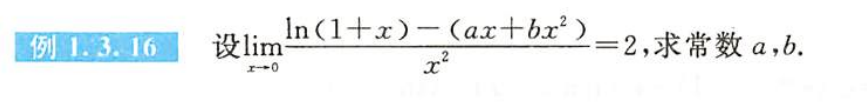
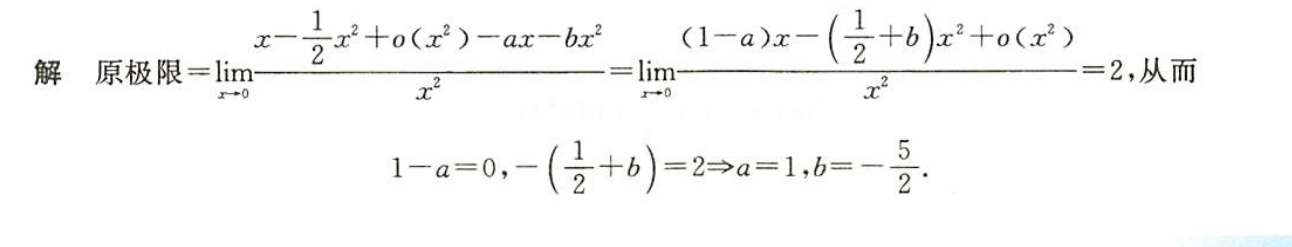




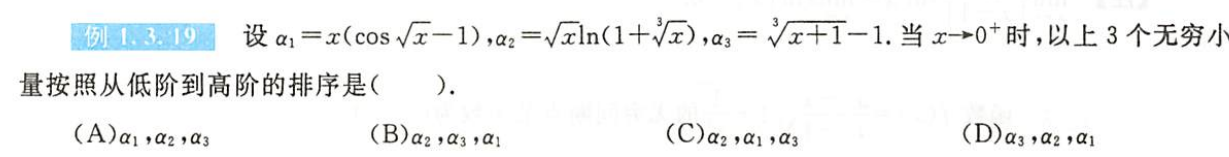

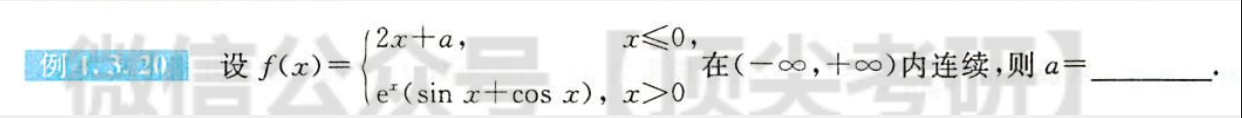
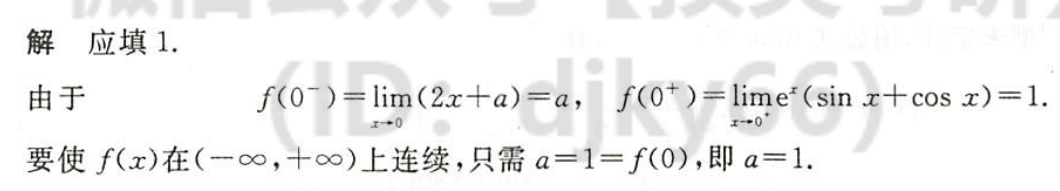
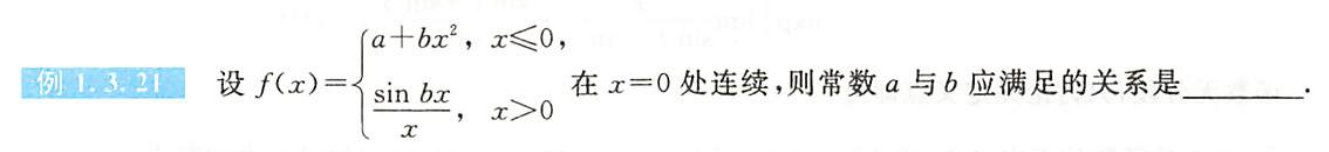
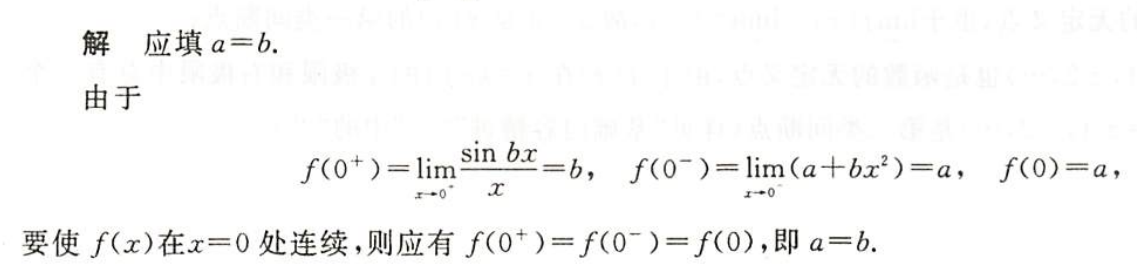






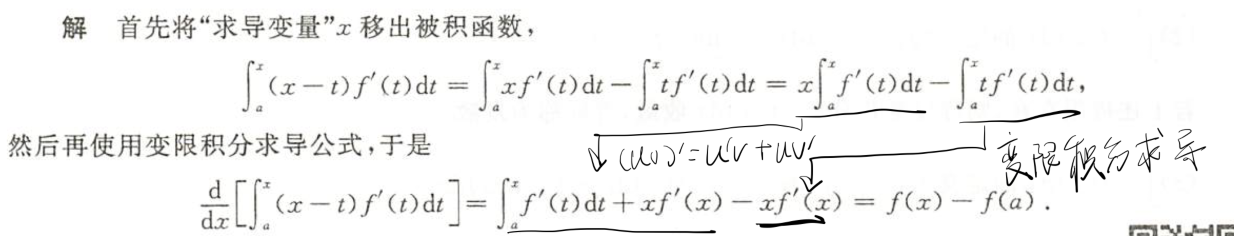








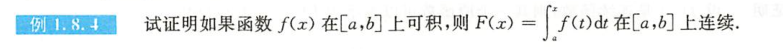


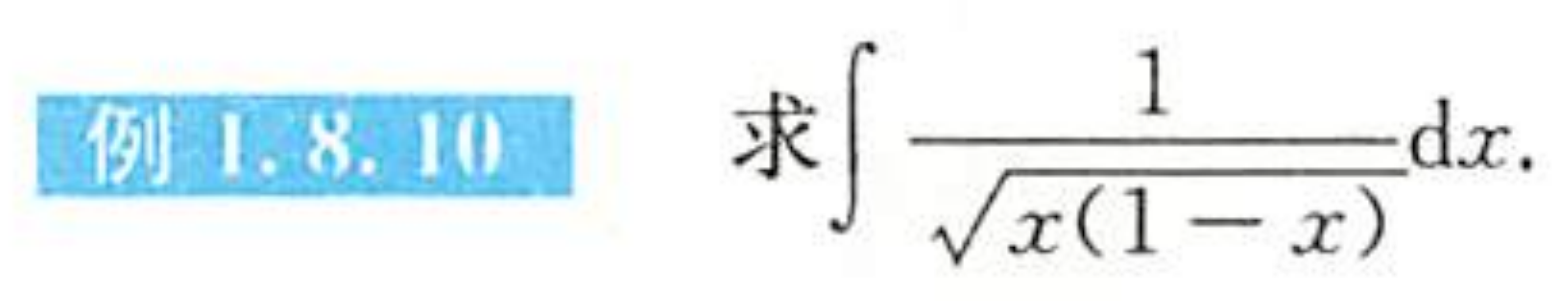
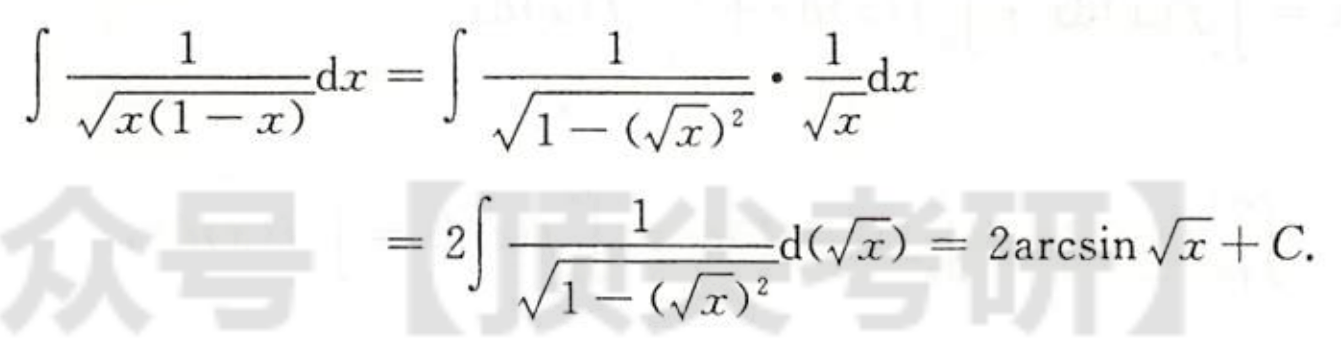
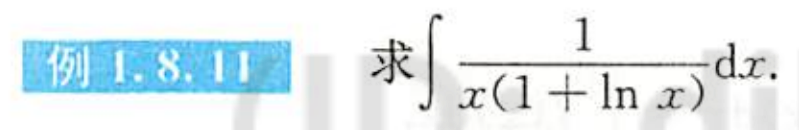
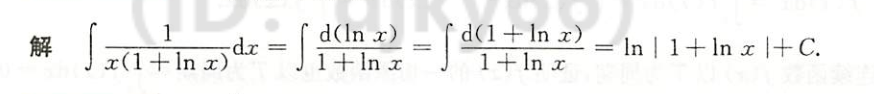
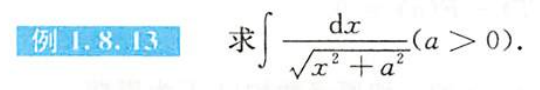
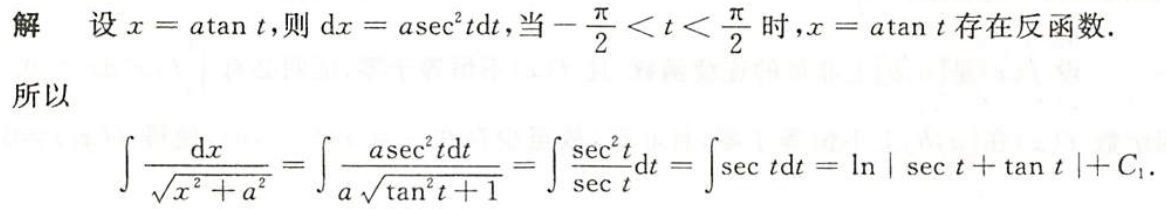
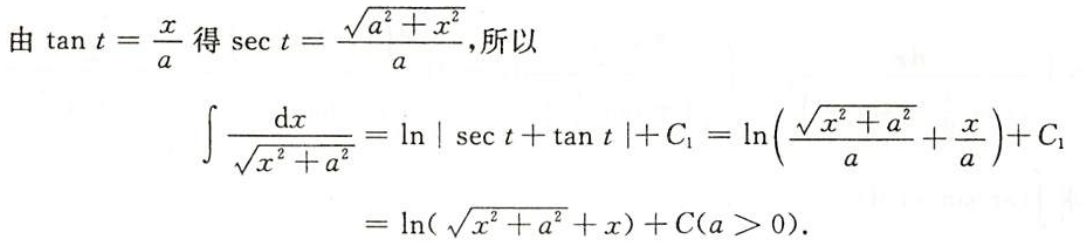
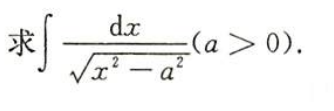
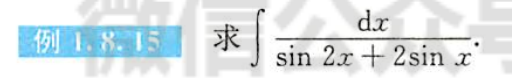
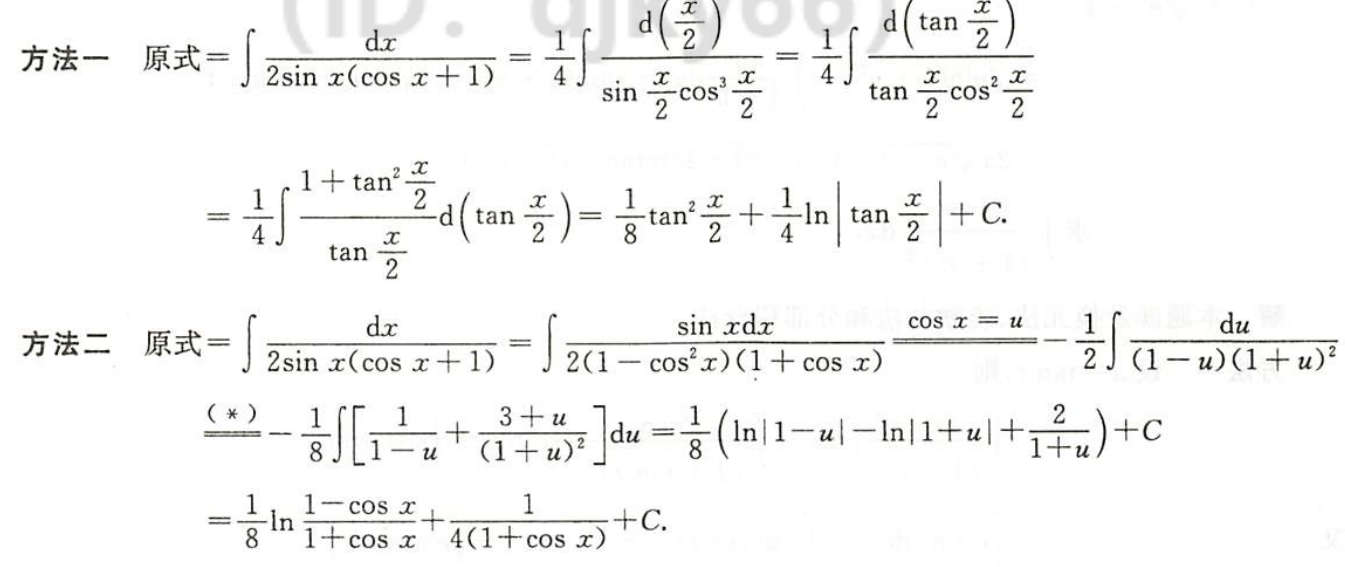


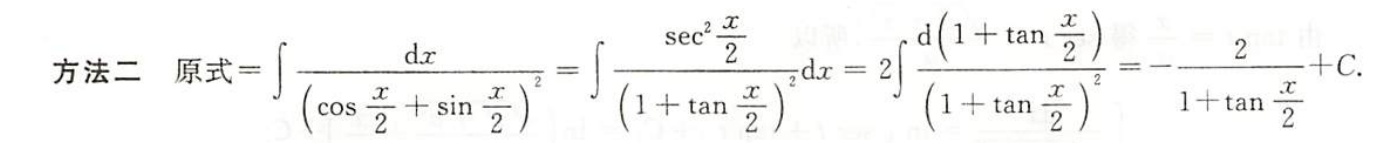
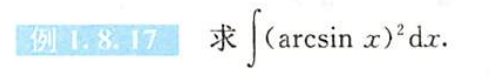

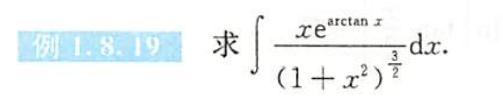
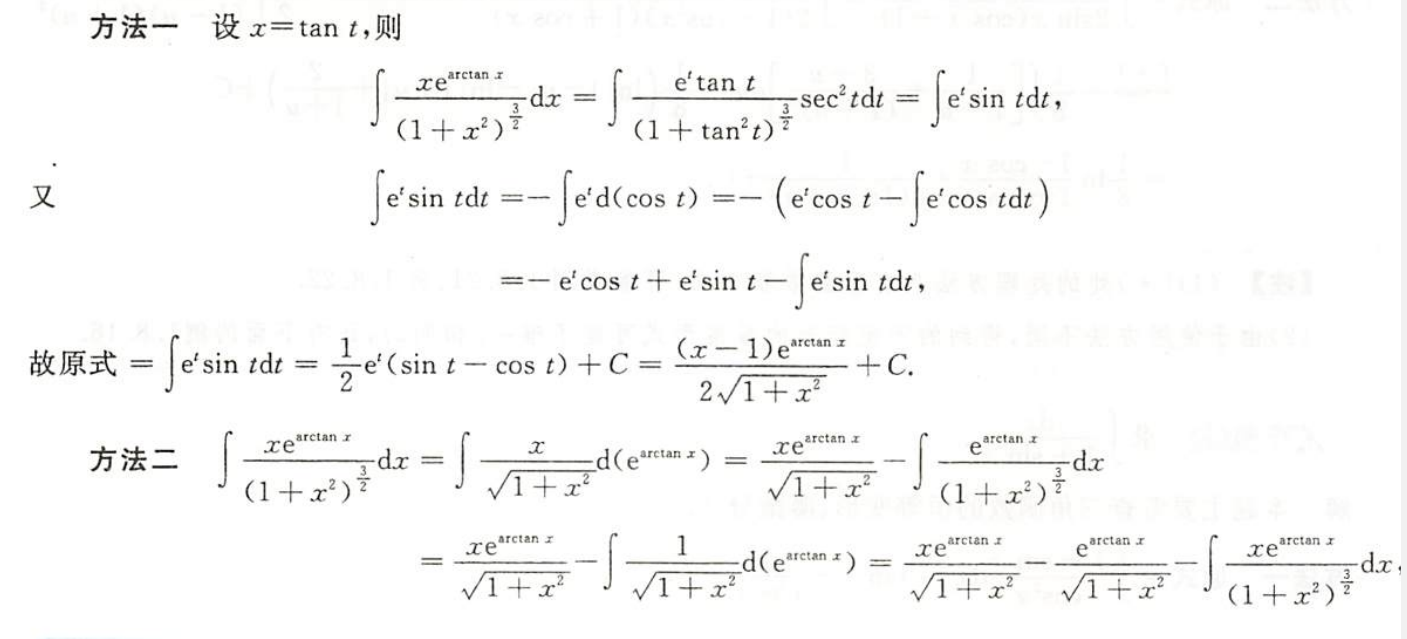
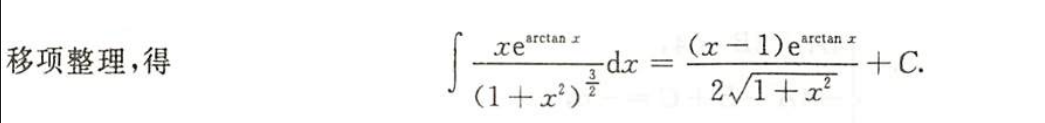


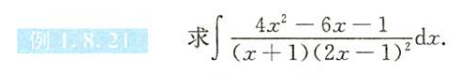


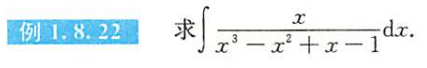
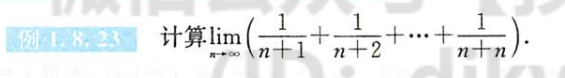

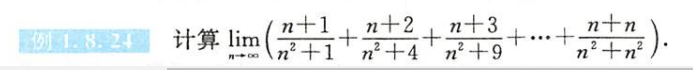

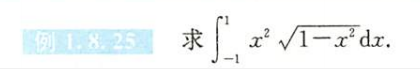





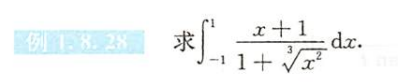


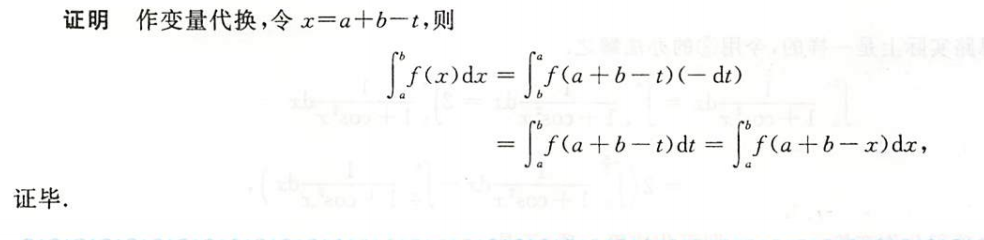


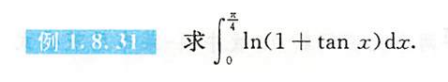
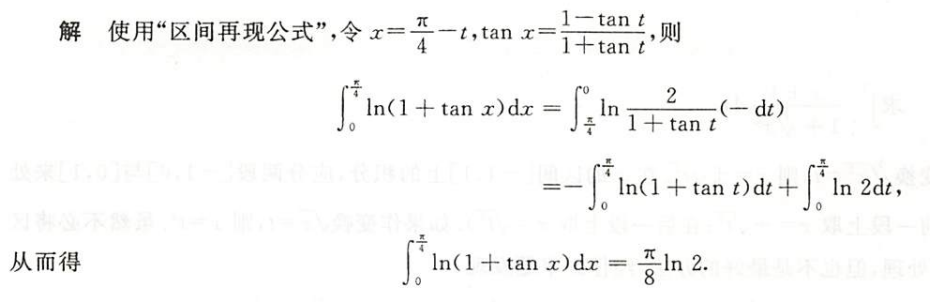
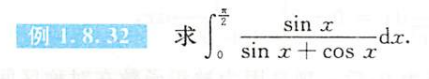


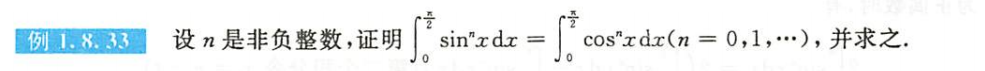





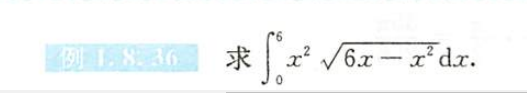
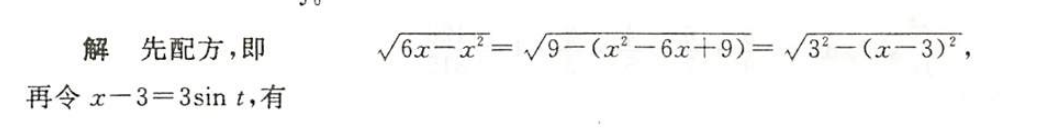
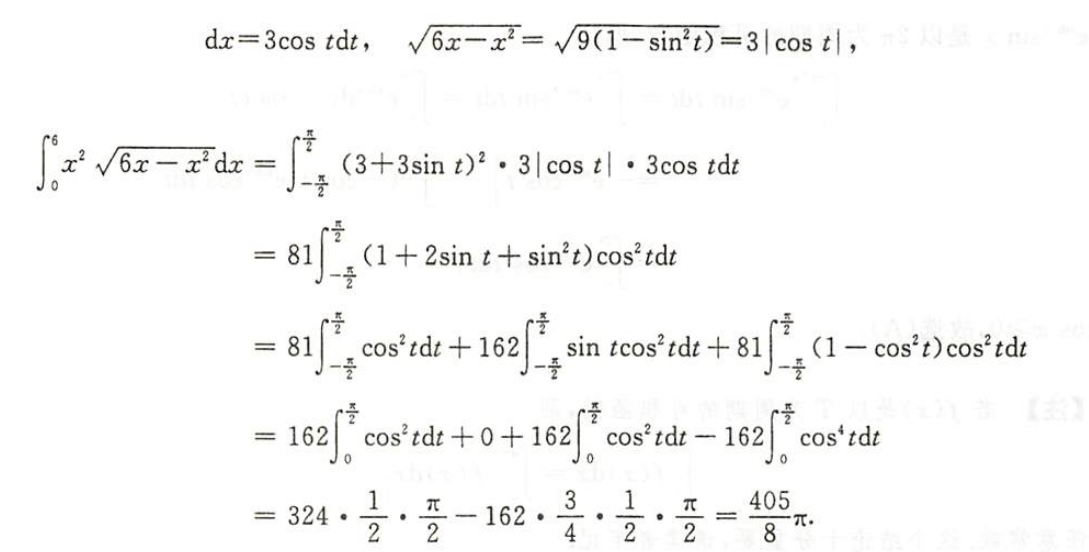
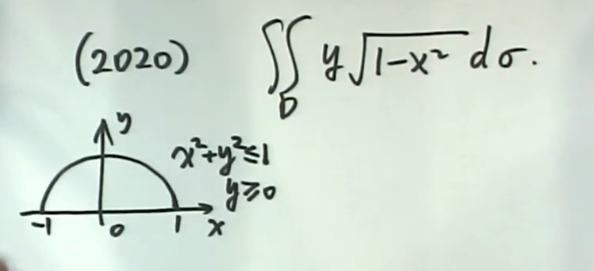
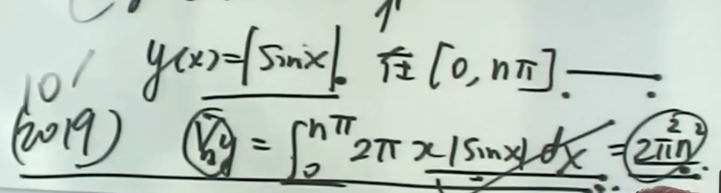
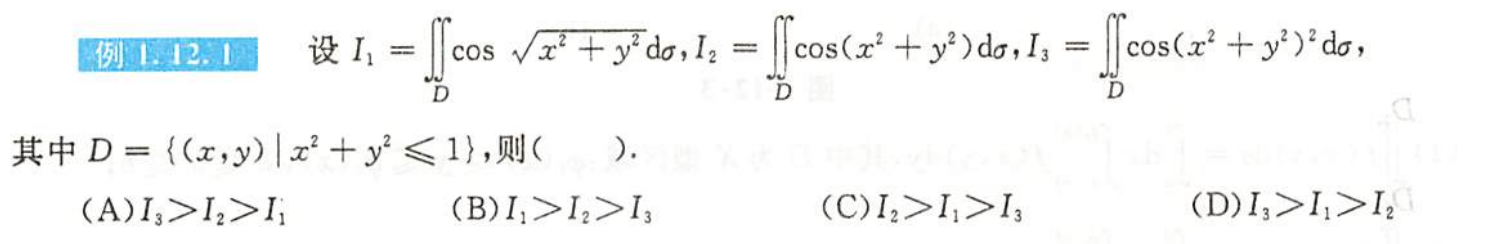


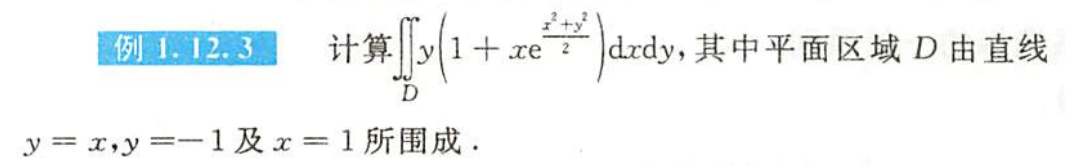

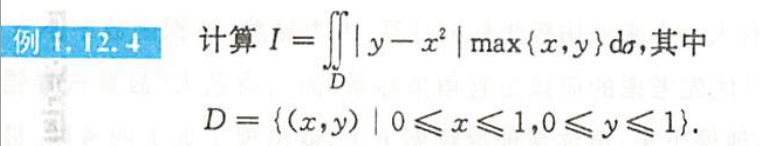

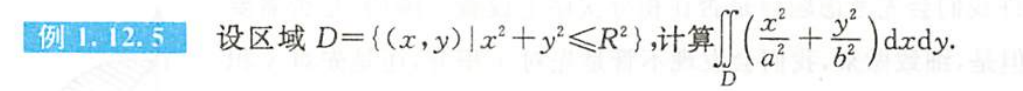

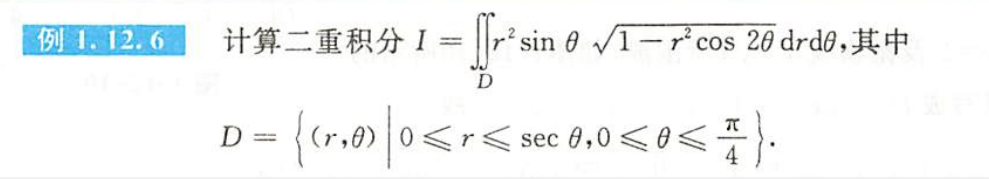


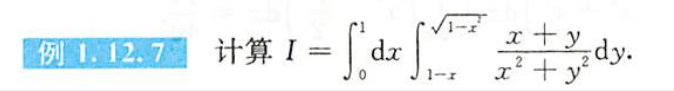

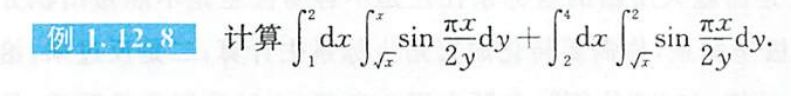
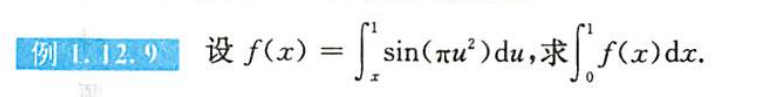
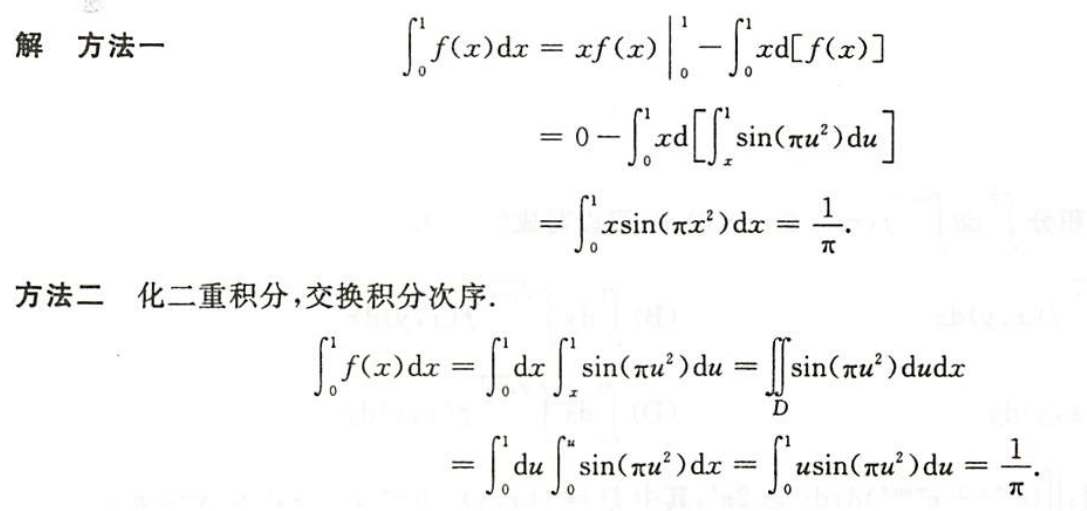

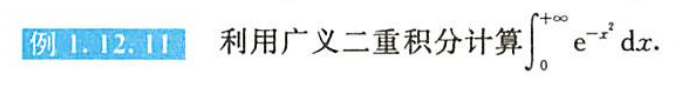



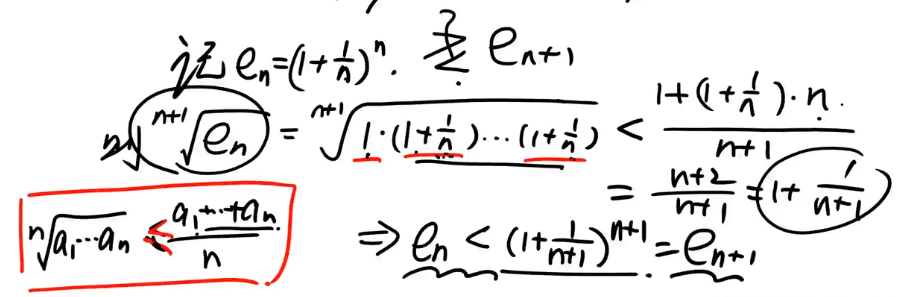
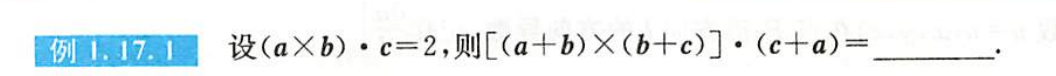
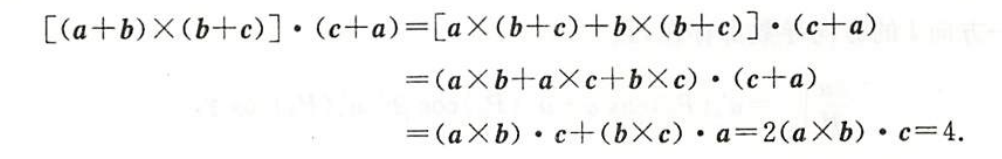


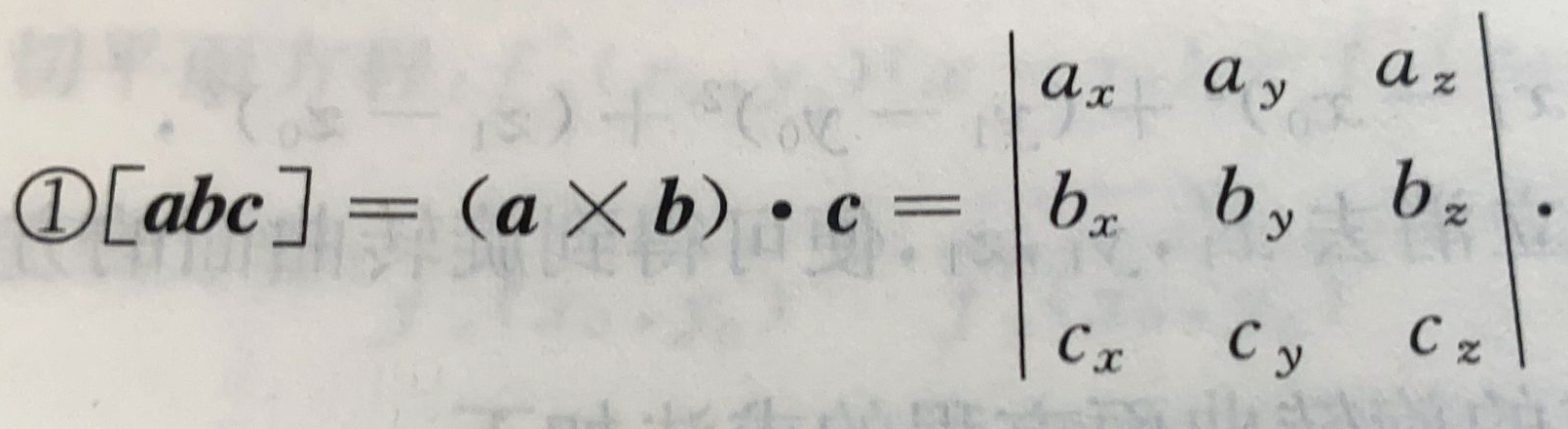
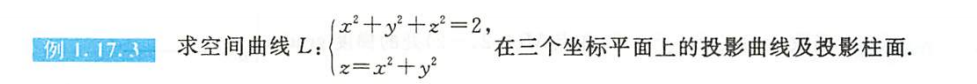

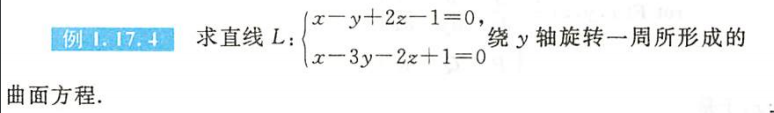

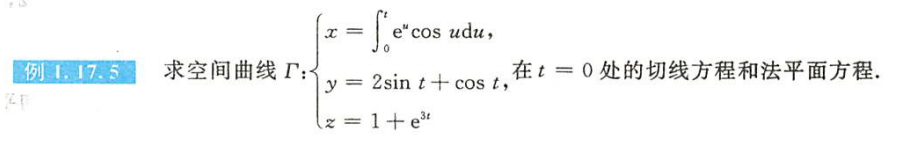
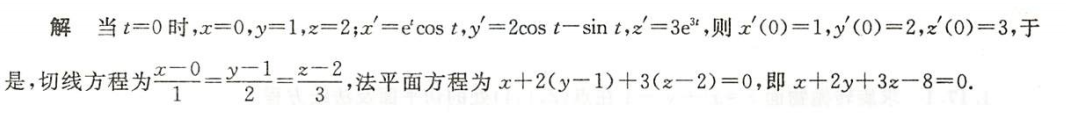

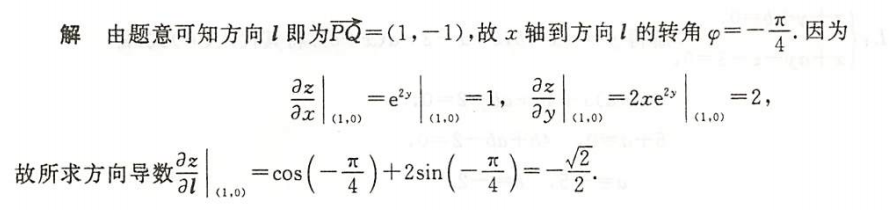
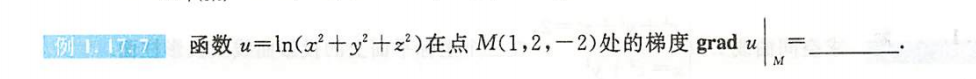
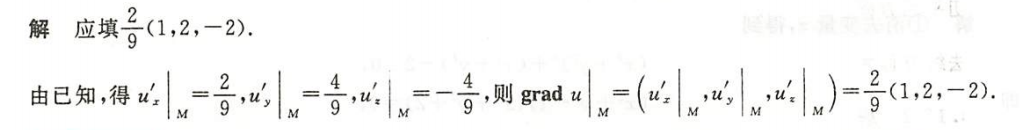
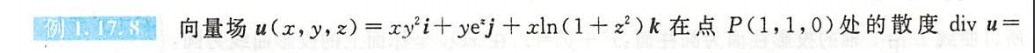
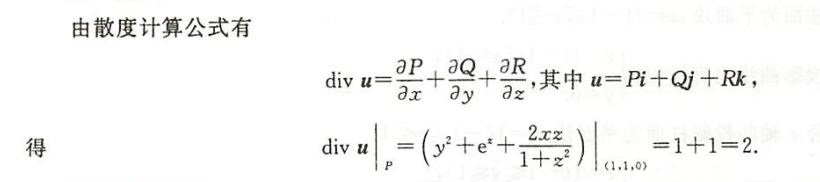
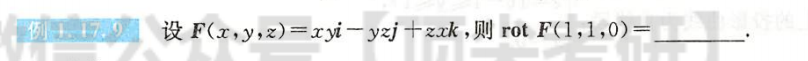

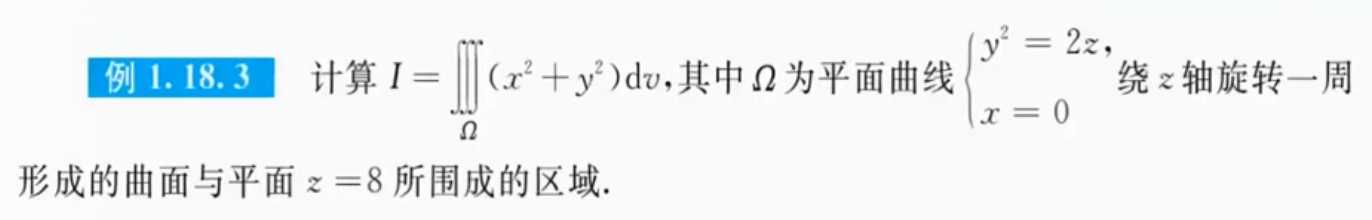
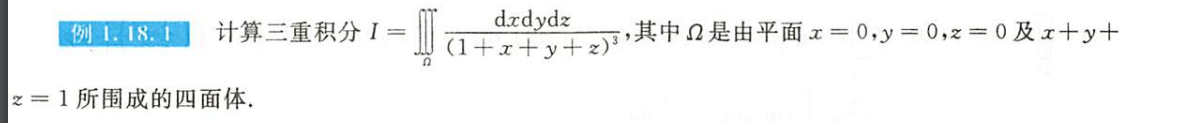


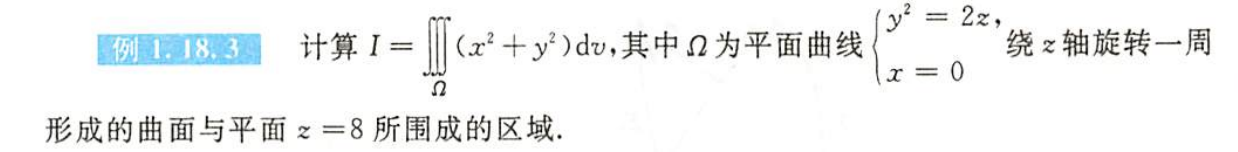

7R4%7EO2PUI42Y.jpg)