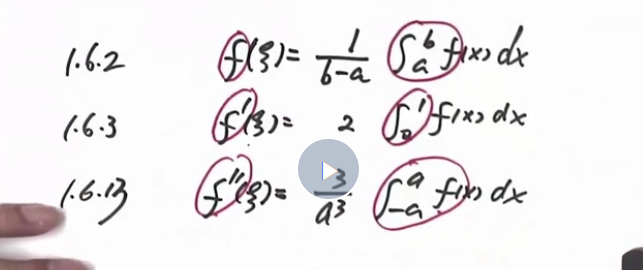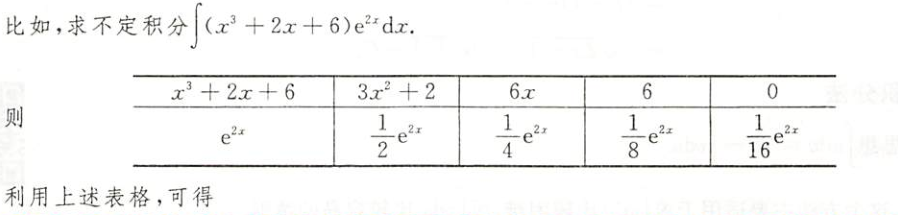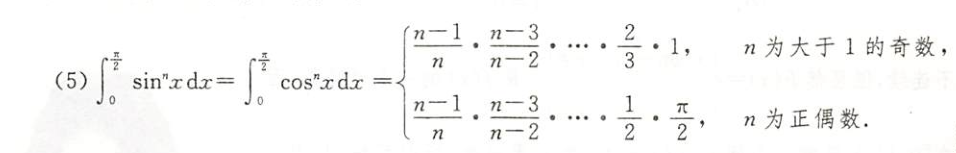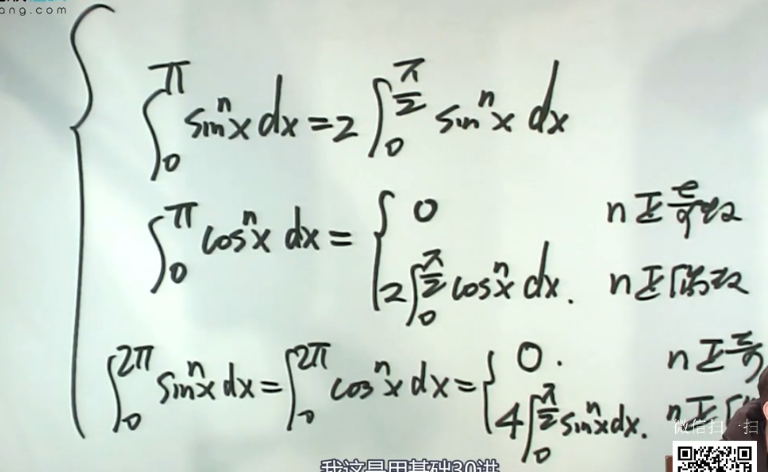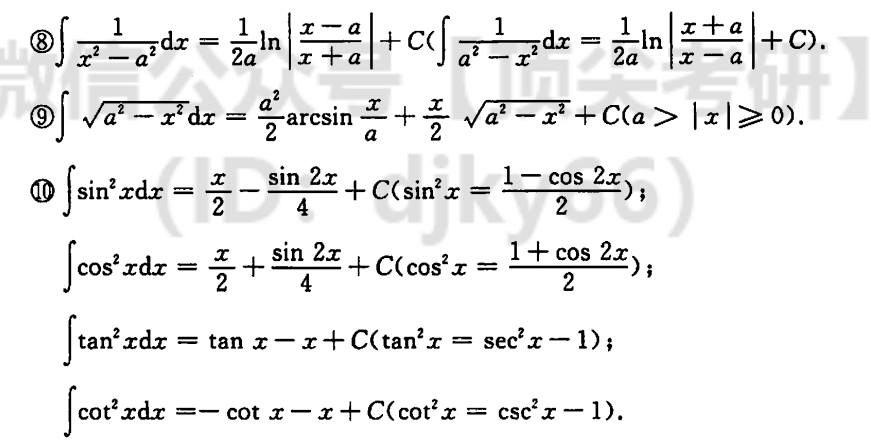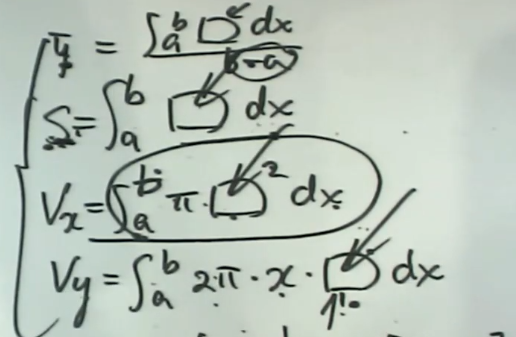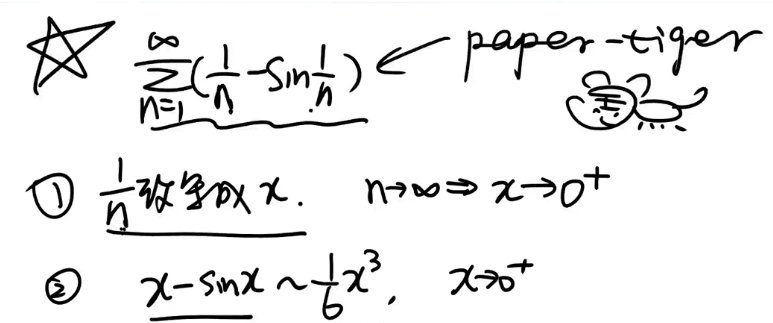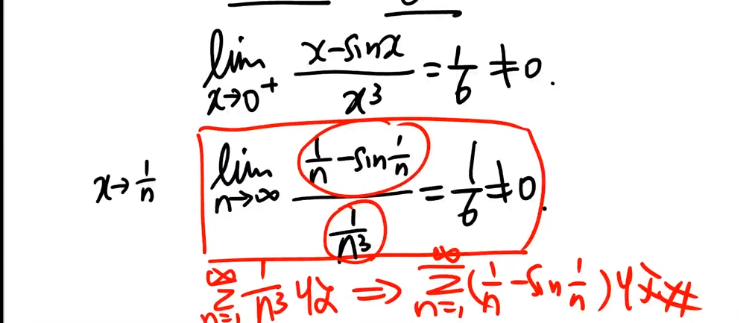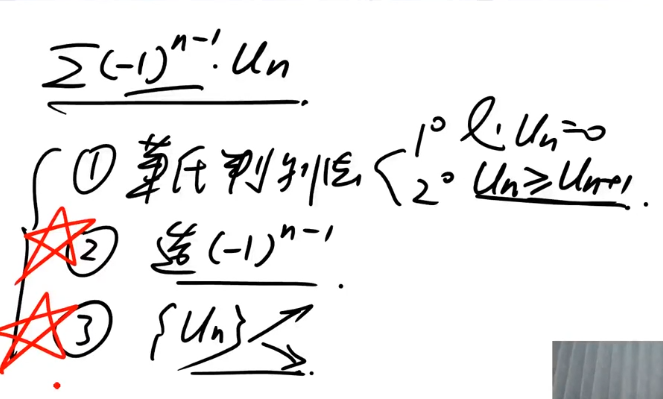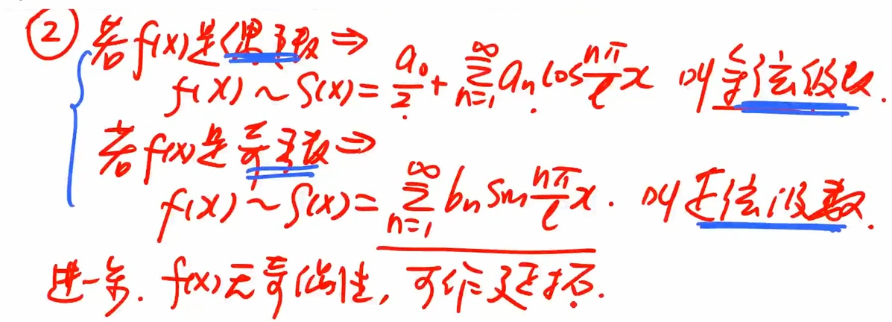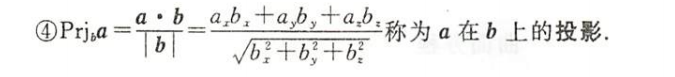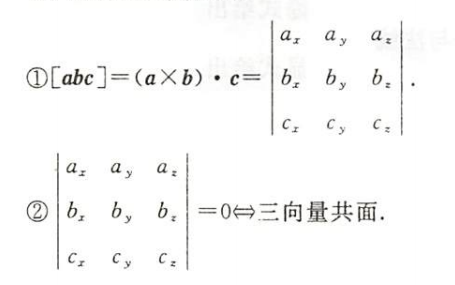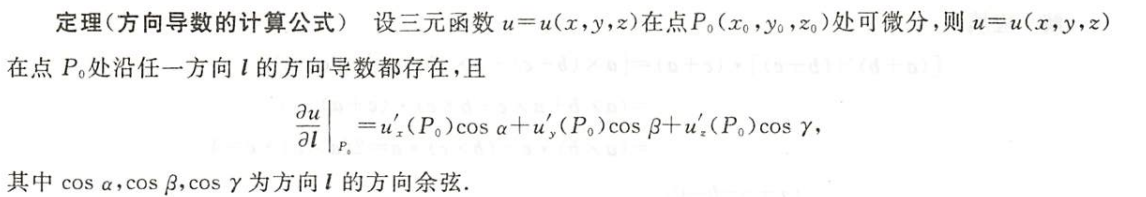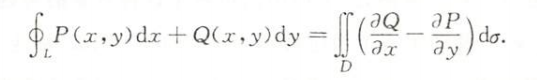30讲高等数学综合

TOC

好好学习

考研数学大纲

• 视频地址
• 术语规范：书本指的是zy2022，课本指的是同济教材

部分结合同济高等数学教材

回答：什么是基础？

定义、定理、性质要清晰

zy2022：2022考研导学

• 考研数学具有稳定性
• 本质和学科素养

历史沿革

莱布尼茨

$\downarrow$

伯努利

$\downarrow$

欧拉

$\downarrow$

拉格朗日

$\downarrow$

柯西

一道例题

• $\dfrac{0}{0}$形：洛必达法则
• $\bigstar$(必出)泰勒公式： 任何可导$f(x) = \sum a_nx^n$,统一成幂函数，统一美
• $\bigtriangledown$ $o(x^3)+o(x^3)=o(x^3)$，这只是一种记号
• $\bigstar$ $\bigstar$ $x-sinx \sim \dfrac{1}{6}x^3(x \to 0)$
  • 打开试卷先找’狗’
  • $sinx \to x^1$
  • $1- cosx \to \dfrac{1}{2}x^2$

复习建议

基础30讲

习题《1000》型A组

《基础习题》200题

36讲

• 高数18讲
• 现代9讲
• 概率9讲

1000bc

zy2022

习题标记含义：
1.4.1：1（高等数学）.4（第四讲）.1 （第一题）

视频锚点

高等数学 ch.1

函数的概念与特性

• 此函数非多值函数

函数$y=f(x)$

反函数$y=f^{-1}(x)$

1. 严格单调函数必有反函数
2. $x=f^{-1}(y)$与$y=f(x)$的图像完全一致。只有把反函数写成$y=f^{-1}(x)$才关于x对称。
   • 可以理解为 $f$ 是一种映射方法，$y=f(x)$ 将x轴的值正向映射到y轴的值, $y=f^{-1}(x)$ 将x轴的值反向映射到y轴的值

复合函数$y=f[g(x)]$

• 掌握复合函数的方法
• 解析
  • 变量广义化
  • 一致单调性
• 值域的解法
  • 画图
  • 配方
  • 求导

$\bigstar$ 四种特性

有界性

• 有界无界必须先指明区间
• 如何证明:找到一个正数$M$使得$|f(x)|\leq M$

单调性

$\mho$(第二点对应的习题)

• 如何证明: $\bigstar$ 求导证明
• 定义法

$\bigstar$ $\clubsuit$ 奇偶性

$\text{设}f(x)\text{是定义在}[-l,l]\text{上的任意函数，则}$

$F_1(x) = f(x) -f(-x) \text{必为奇函数},F_2(x)=f(x)+f(-x) \text{必为偶函数}$

$\text{显然}u(x)=\dfrac{1}{2}[f(x)+f(-x)]\text{是偶函数,} \dfrac{1}{2}[f(x) -f(-x)]\text{是奇函数,}\text{而}$

$f(x) = \dfrac{1}{2}[f(x)+f(-x)] + \dfrac{1}{2}[f(x) -f(-x)]=u(x)+v(x)$

奇函数在0点有定义，$f(0)=0$

偶函数在0点有定义，$f’(0)=0$

$\text{函数}y=f(x)\text{与}y=-f(x)\text{的图形关于x轴对称;函数}y=f(x)\text{与}y=f(-x)\text{的图形关于y轴对称；函数}y=f(x)\text{与}y=-f(-x)\text{的图形关于原点对称}$

函数$y=f(x)$的图形关于直线$x=T$对称的充分必要条件是

$$f(x)=f(2T-x)\text{或}f(x+T)=f(T-x)$$

周期性

$\bigstar$ $\bigstar$ $\bigstar$ $\spadesuit$(p6:必考) 7个重要结论

求导之后奇偶性互换

$\sharp$ 拉格朗日中值有什么用:

用导数的大小控制函数的大小

$\bigstar$ $\bigstar$ $\bigstar$ 函数的图像

$\bigtriangledown$ 用微分法和积分法研究函数的性态和测度

直角坐标系下的图像($f(x,y)=0$)

常见图像

基本初等函数与初等函数

基本初等函数：常数函数+反对幂指三

${\textstyle\unicode{x2460}}$见到$\sqrt{u},\sqrt[3]{u}$,用$u$研究最值

$\bigstar$ ${\textstyle\unicode{x2461}}$见到$|u|$用$u^2$研究最值

${\textstyle\unicode{x2462}}$ 见到$\dfrac{1}{u}$,用$u$即可研究最值，$u>0$

$$\bigstar {\textstyle\unicode{x2463}}\text{见到} u_1 u_2 \cdots u_n = u \text{用} ln u = \displaystyle\sum_{i=1}^n ln u_i$$

• 指数函数

• 对数函数
  $\bigstar$(100%要做第二个变换) 恒等变换$x=e^{ln x},u^v=e^{ln u^v}=e^{v ln u}$

• 三角函数

• 反三角函数

  • $sinx$取$-\dfrac{\pi}{2}$到$\dfrac{\pi}{2}$区间做变换
  • $cos x$取$0$到$\pi$区间做变换
  • $f(x)=arcsin(x)+arccos(x)=\dfrac{\pi}{2}$
    • $f’(x)=\dfrac{1}{\sqrt{1-x^2}}-\dfrac{1}{-\sqrt{1-x^2}} \equiv 0$
    • 拉：$f(b)-f(a)=f’(g)(b-a)$
• $\bigtriangledown$ $xe^x,xln(x),x^x$随手就能画出来
• 取整函数
  • $x-1<[x]<x$
• 常见图像要不假思索的画出来

图像变换

平移变换

• 自变量变换：左加右减

对称变换

• 添负号
• 函数添加绝对值
• $\bigstar$ 自变量加绝对值

伸缩变换

• 自变量kx，横坐标缩小$\dfrac{1}{k}$

$\spadesuit$(p13:极坐标系下的图像) 极坐标系下的图像($g(r,\theta)=0$)

用描点法画常见图像

$\bigstar$ 心形线

• $r=a(1-cos(\theta))$
• 外摆线的一种

玫瑰线

• $r=a\cdot sin(3\theta)$

阿基米德螺线

• $r=a\cdot \theta(a>0.\theta\leq 0)$

伯努利双扭线

• $r^2=2a^2cos(2\theta)$

用直角系观点画极坐标系下图像

• 感觉好像没有想象中的那么流畅？
• 如果r随角度增大是很明显的螺旋线

参数法——参数方程

$$\left( \{ \begin{array}{cc} x = x(t)\\ y=y(t) \end{array} \right)$$

$\bigstar$ 摆线

$$\{ \begin{array}{cc} x = r(t-sin(t))\\ y=r(1-cos(t)) \end{array}$$

• 平摆线(在地平摆动的线)
• 周期是$\pi r$

$\bigstar$ 星形线

$$\{ \begin{array}{cc} x = r\cdot cos^3t\\ y=r\cdot sint^3t \end{array}$$

• 内摆线

$\spadesuit$(p23:1.1.4，p24答案) 对数螺线

$r=ae^{k\theta}$

常用基础知识

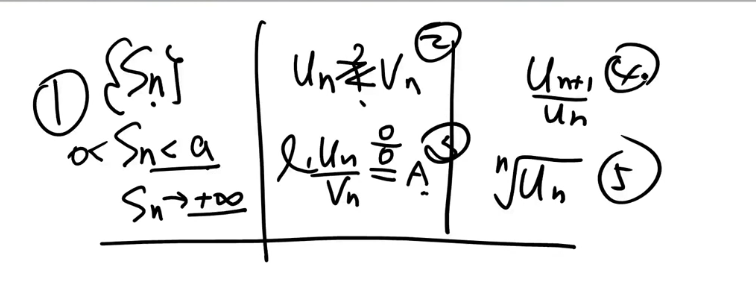
数列

等差数列

首项为$a_1$，公差为$d$(d $\neq$ 0)的数列$a_1,a_1+d,\cdots,a_1+(n-1)d$

${\textstyle\unicode{x2460}}$ 通项公式 $a_n=a_1+(n-1)d$

${\textstyle\unicode{x2461}}$ 前$n$项的和$S_n=\dfrac{n}{2}[2a_1+(n-1)d]=\dfrac{n}{2}(a_1+a_n)$

$\bigstar$ 等比数列

首项为$a_1$,公比为$r(r\neq0)$的数列$a_1,a_1r,a_1r^2,\cdots,a_1r^{n-1}$

${\textstyle\unicode{x2460}}$ 通项公式$a_n=a_1r^{n-1}$

${\textstyle\unicode{x2461}}$ 前$n$项的和(n从1开始数，$\color{red}{\text{记忆}}$读法：首项乘以(1-公比的n次方)，除以1-公比)

$$S_n = \begin{cases} na_1 ,& r=1, \\ \dfrac{a_1(1-r^n)}{1-r} ,& r\neq 1, \end{cases}$$

• 若$|r|<1 \implies \displaystyle\lim_{n \to \infty} \dfrac{1-r^n}{1-r}=\dfrac{1}{1-r}$

一些常见数列前$n$项和

${\textstyle\unicode{x2460}}$ $\displaystyle \sum_{k=1}^n k=1+2+3+\cdot+n=\dfrac{n(n+1)}{2}$

${\textstyle\unicode{x2461}}$ $\displaystyle \sum_{k=1}^n k^2=1^2+2^2+3^2+\cdot+n^2=\dfrac{n(n+1)(2n+1)}{6}$

${\textstyle\unicode{x2462}}$ $\displaystyle \sum_{k=1}^n \dfrac{1}{k(k+1)}=\dfrac{1}{1 \times 2}+ \dfrac{1}{2 \times 3} + \dfrac{1}{3 \times 4} +\cdot+\dfrac{1}{n \times (n+1)}=\dfrac{n}{n+1}$ (列项相消)

三角函数

三角函数的基本关系

• $sec \alpha = \dfrac{1}{cos \alpha}$
• $1+tan^2=sec^2\alpha$
• $csc \alpha = \dfrac{1}{sin \alpha}$
• $cot \alpha = \dfrac{1}{tan \alpha}$

诱导公式

$\bigstar$(换元常用，自己一开始没怎么理解) 8点,奇变偶不变，符号看象限

• $sin(\dfrac{\pi}{2} \pm \alpha) = cos\alpha$
• $cos(\dfrac{\pi}{2} \pm \alpha) = \mp sin\alpha$
• $sin(\pi \pm \alpha) = \mp sin\alpha$
• $cos(\pi \pm \alpha) = - cos\alpha$

重要的公式

倍角公式

• $sin 2\alpha=2sin\alpha cos\alpha$
• $cos2\alpha=cos^2-sin^2=1-2sin^2\alpha=2cos^2\alpha-1$
• $sin 3\alpha = -4sin^2\alpha+3sin\alpha$

$\bigstar$(真题) $\text{当}x\to 0\text{时,}3sin3x-sin3x \backsim cx^k,c=?,k=?$

• 解法1：泰勒展开，幂次最低原则展开
• 解法2：$sin 3\alpha = -4sin^2\alpha+3sin\alpha$

和差公式

$tan(\alpha \pm \beta)=\dfrac{tan\alpha \pm tan \beta}{1 \mp tan\alpha tan\beta}$

• $tan(\dfrac{\pi}{4}+\alpha)$

$sin(\alpha \pm \beta)=sin\alpha cos\beta \pm cos \beta sin \alpha$

万能公式

指数运算法则

$\bigstar$ $\bigstar$ $\bigstar$(多项相乘，相除，乘方，开方) 对数运算法则

• $\spadesuit$(p65:1.4.19) $y=\sqrt[3]{\dfrac{(x+1)(2x-1)^2}{(4-3x)^5}},\text{求}y’$
  • 加绝对值取对数
• 统计学里的极大似然估计法
• 见到$ln(1+\dfrac{1}{x})$ $\spadesuit$(p21:常用不等式(10))
  • 拉格朗日

一元二次方程基础

${\textstyle\unicode{x2460}}$ 一元二次方程$ax^2+bx+c=0(a\neq 0)$

${\textstyle\unicode{x2461}}$根的公式$x_{1,2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

• 讲微分方程的时候会用到加上虚部i, 共轭复根

${\textstyle\unicode{x2462}}$ 根与系数的关系(韦达定理)$x_1+x_2=-\dfrac{b}{a},x_1x_2=\dfrac{c}{a}$

因式分解公式

• $(a+b)^3=a^3+3a^2b+3ab^2+b^3$
  • 系数记忆方法：1331
• $(a-b)^3=a^3-3a^2b+3ab^2-b^3$
• 二项定理$(a+b)^n=\displaystyle \sum_{k=0}^nC_n^ka^{n-k}b^k$
  • 次消彼长
• $a^3+b^3 = (a+b)(a^2-ab+b^2)$

阶乘与双阶乘

• $(2n)!!=2\cdot4\cdot6\cdot \cdots \cdot(2n)=2^n\cdot n!$
• $(2n-1)!!=1\cdot3\cdot5\cdot \cdots \cdot(2n-1)$
  • $\bigstar$ $\bigstar$ $\bigstar$(必考) 华里士公式(点火公式)
  • 如: $\int_0^{\frac{\pi}{2}}sin^{10}xdx=\dfrac{9}{10}\dfrac{7}{8}\dfrac{5}{6}\dfrac{3}{4}\dfrac{1}{2}\dfrac{\pi}{2}$
  • 如: $\int_0^{\frac{\pi}{2}}cos^{9}xdx=\dfrac{8}{9}\dfrac{6}{7}\dfrac{4}{5}\dfrac{2}{3}$

$\bigstar$ $\bigstar$ $\bigstar$ 常用不等式

$\spadesuit$(p？:例1.2.2) 设a,b为实数，则 ${\textstyle\unicode{x2460}}$ $|a\pm b| \leq |a|+|b|$; ${\textstyle\unicode{x2461}}$ $||a|-|b|| \leq |a-b|$ $\spadesuit$(p?:例1.2.2)

• 函数的极限和绝对值极限的关系
• 推广：离散，连续情况
• 绝对值不等式的记忆方法：其实稍微推导一下是很显然的对于2式子只需考虑，左边的最大比右边的最小要小即可(即符号相同，其实左边的差无所谓符号)
• 由此可以归纳出，绝对值有让数字变大的趋势，绝对值的差会让数字变小

${\textstyle\unicode{x2460}}$ $\sqrt{ab}\leq \dfrac{a+b}{2} \leq \sqrt{\dfrac{a^2+b^2}{2}}$ $\spadesuit$(p?:例题1.1.4)

• 几何平均值小于算数平均值

高等数学 ch2.数列极限

p32

数列极限

• 求极限（或证明极限的存在性）

引言

• 极限，是一个”无限趋近的过程“
  • 注意是过程，不是值

定义法解极限题目	要点
	$\spadesuit$(p27:例1.2.1) $\spadesuit$(p29:习题1.2.1)三部曲 ${\textstyle\unicode{x2460}}$ 先写距离$\lvert x_n-a\rvert < \varepsilon$(先写距离，数列通项减去a，加绝对值) ${\textstyle\unicode{x2461}}$ 反解出$n>g(\varepsilon)$ ${\textstyle\unicode{x2462}}$ 取$N=[g(\varepsilon)]+1$

用定义

设$\lbrace x_n \rbrace$为一数列，如果存在常数$a$,对于任意给定的正数$\varepsilon$(无论它多么小),总存在正整数$N$，使得当$n>N$时,不等式$\lvert x_n -a \rvert < \varepsilon$都成立，那么就称常数$a$是数列$\lbrace x_n \rbrace$的极限，或者称数列$\lbrace x_n \rbrace$收敛于$a$,记为

$$\displaystyle \lim_{n \to \infty}x_n =a \quad \text{或} \quad x_n \to a(n \to \infty)$$

---

1. ‘$\varepsilon-N$语言’
2. 数列与子列的关系

$\spadesuit$(p？:例题1.2.2)若原极限存在，则加绝对值的极限也存在

由绝对值不等式$||a|-|b|| \leq |a-b|$

但是注意右不能推左,即若加绝对值的极限也存在,原极限可能不存在

$$\text{除非}A=0，\bigstar \displaystyle\lim_{n \to \infty}a_n=0 \iff \displaystyle \lim_{n \to \infty}|a_n|=0$$

夹逼定理可以用绝对值，省去了一半的功夫

一个命题的逆否命题可以用来帮助判断(德摩根定律)

判断数列是否收敛的两个方法，用逆否命题

• 取一个子数列不收敛
• 取两个子数列没有收敛到一个数

用定义解题总结: 当给定极限为几的时候，要你证明可以尝试要用定义法

$\spadesuit$(p27:收敛数列的性质) 用性质

定理1 唯一性

给出数列${xn}$,若$\displaystyle\lim{n\to \infty}x_n=a$(存在)，则$a$是唯一的

定理2 有界性

若数列${x_n}$极限存在，则数列${x_n}$有界

定理3 $\bigstar$(脱帽法) 保号性

设数列$\lbrace a_n \rbrace$存在极限$a$,且$a>0$(或$a<0$),,则存在正整数$N$，当$n>N$时，有$a_n>0$(或$a_n<0$)

推论 如果数列${an}$从某项起有$a_n\geq 0$,且$\displaystyle\lim{n\to \infty}a_n=a$,则$a\geq 0$

---

(脱帽法)不带等号

$\displaystyle\lim_{n\to \infty}a_n=a>0 \implies a_n>0$

(戴帽法)通项大于0，极限(加上了帽子的限制)也大于0，始终带有一个等号

$$a \geq 0 \impliedby \begin{cases} a_n \geq 0 \\ \text{且} \displaystyle \lim_{n \to \infty} a_n =a \end{cases}$$

• 即使通项严格大于零，极限有可能是0

用数列极限运算法则

数列极限的运算法则如下,即加减乘除的极限等于极限的加减乘除

设$\displaystyle \lim{n \to \infty}x_n=a,\quad \displaystyle \lim{n \to \infty}y_n=b$

$\displaystyle \lim_{n \to \infty}(x_n\pm y_n)=a \pm b$

$\displaystyle \lim_{n \to \infty}x_n y_n=ab$

$\displaystyle \lim_{n \to \infty}( \dfrac{x_n}{y_n} )=\dfrac{a}{b}$

推论

如果$\lim f(x)$存在，而$c$为常数，那么$\lim \lbrack cf(x) \rbrack = c\lim f(x)$

如果$\lim f(x)$存在，而$n$为正整数，那么$\lim \lbrack f(x) \rbrack^n = [\lim f(x)]^n$

---

注意不能拆，反例分析：

$$\displaystyle \lim_{n \to \infty}(a_n + b_n) = 1 \nRightarrow \displaystyle \lim_{n \to \infty} a_n +\displaystyle \lim_{n \to \infty} b_n = 1$$

例如：$a_n=(-1)^n,b_n=-(-1)^n+1$

但是已经存在是可以直接用$\spadesuit$(p？:例题1.2.4)

用数列极限运算法则解题总结：emmm，一般不会单独出吧

$\bigstar$ 用夹逼准则

如果数列${x_n},{y_n},{z_n}$满足

${\textstyle\unicode{x2460}}$ $y_n \leq x_n \leq z_n(n=1,2,3,\cdots)$

${\textstyle\unicode{x2461}}$ $\displaystyle lim{n\to \infty}y_n=a,\quad \displaystyle lim{n\to \infty}z_n=a$

则数列${xn}$的极限存在，且$\displaystyle lim{n\to \infty}x_n=a$

---

夹：夹逼准则不验证等号

逼：’哪里跑’

$\spadesuit$(p28:例题1.2.5)

经典的把分母放大缩小

$\spadesuit$(p？:习题1.2.2)

$\bigstar$(考研真题) $\spadesuit$(p？:习题1.2.3)

只变分母不变分子

用夹逼准则解题：表达式可以很好的放缩

$\bigstar$ $\bigstar$ $\bigstar$(考研数学压轴题的考点) 用单调有界准则

单调有界数列必有极限，即若数列${xn}$单调增加(减少)且有上界(下界),则$\displaystyle \lim{n \to \infty}x_n$存在

---

• 单调有界数列必有极限

证明数列单调的两个方法

• 做差$x_{n+1}-x_n$
• 做比$\dfrac{x_{n+1}}{x_n} \leq 1$(同号)

$\spadesuit$(p？:1.2.6 和1.2.7)

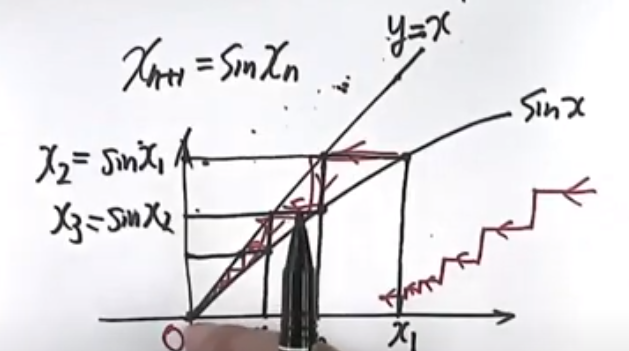
$\bigstar$ 见到递推式 $a_{n+1}=f(a_n)$一般用单调有界准则 $\mho$(还有一些别的方法)

$\blacktriangleright$(为什么还要证明$A\geq \sqrt{2}$))例题1.2.6没怎么看懂，因为求出来有正负两个值

$\bigstar$(真题) $\spadesuit$(p？:1.2.7) 取无数次sin $\spadesuit$(p21: $sinx<x$)
数学分析的思想：用迭代逼近一个数

$\flat$ $\spadesuit$(p？:例1.2.4) $\spadesuit$(p18:裂项相消)

$\bigstar$(求极限的另外一个方法直接计算出来(直接计算算法，考验恒等变化)) $\spadesuit$(p？:例题1.2.6 ) 二阶递推变成1阶递推 ,裂项相消的逆运算

用单调有界准则解题总结:
分三步

• 证明单调：
  • 求导
  • 做差的极限小于0
• 证明有界：
  • 不等式
• 求极限值：
  • 等式两边取极限

适用题型:给递推式

用定积分的定义

如例1.8.23

高等数学 ch3.函数极限与连续性

p39

$\bigstar$(学习方法) 对知识结构的把握，纲举目张

运算法则-无穷小比阶来研究7种未定式计算

函数极限

方法一览

定义

局部有界性

局部保号性

---

强调计算

领域

一维的情况

可以叫区间

• 领域：以$x_0$为中心的任何开区间称为点$x_0$的领域，记作$U(x_0)$
• $\delta$领域：记作$U(x_0,\delta)$
• 去心$\delta$领域：记作$\mathring{U}(x_0,\delta)$

二维的情况

以$p$为圆心，圆内的点就是其领域，可以叫区域

• $\delta$领域：记作$U(p_0,\delta)$

定义

设函数$f(x)$在点$x_0$的某一去心领域内有定义.如果存在常数$A$，对于给定的正数$\varepsilon$(无论它多么小)，总存在正数$\delta$,使得$x$满足不等式$0 \lvert x-x_0 \rvert < \delta$时，对应的函数值$f(x)$都满足不等式

$$\lvert f(x) -A \rvert < \varepsilon$$

那么常数$A$就叫做函数$f(x)$当$x \to x_0$时的极限，记作

$$\lim_{x \to x_0}f(x)=A \text{或} f(x) \to A \quad (\text{当}x \to x_0)$$

可以简单的表述为

$$\lim_{x \to x_0}f(x) = A \iff \forall \varepsilon >0, \exists \delta > 0,\text{当}0< \lvert x - x_0\rvert < \delta \text{时，有} \lvert f(x)-A \rvert < \varepsilon$$

左极限：

$$\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists \delta > 0,\text{当} x_0 - \delta < x <x_0 \text{时，有} \lvert f(x)-A \rvert < \varepsilon$$

右极限：

$$\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists \delta > 0,\text{当} x_0 < x < x_0 - \delta \text{时，有} \lvert f(x)-A \rvert < \varepsilon$$

自变量趋于无穷大的极限：

$$\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists X > 0,\text{当} \lvert x \rvert > X \text{时，有} \lvert f(x)-A \rvert < \varepsilon$$

自变量趋于负无穷大的极限:

$$\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists X > 0,\text{当} x < -X \text{时，有} \lvert f(x)-A \rvert < \varepsilon$$

自变量趋于正无穷大的极限:

$$\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists X > 0,\text{当} x > X \text{时，有} \lvert f(x)-A \rvert < \varepsilon$$

---

‘$\varepsilon-\delta$语言’

‘$\varepsilon-X$语言’,总共四种要整理一下

极限和函数的值没有任何关系

脱帽法

无穷小的阶数是可以计算的

性质

$\bigstar$(真题) $\spadesuit$(p？:例题1.3.1)

• 考虑趋向于$0^+和0^-的两种情况$
• 极限的和等于和的极限的前提 $\mho$(前提是啥来着)

唯一性 $\bigstar$

如果$\lim_{x \to x_0}\text{存在}$,那么这极限唯一

局部有界性 $\bigstar$

如果$\lim_{x \to x_0}f(x)=A,$那么存在常数$M>0$和$\delta>0$,使得当$0< \lvert x - x_0 \rvert < \delta\text{时，有}\lvert f(x) \rvert \leq M$

---

• 有限个有界的函数和差积依然是有界函数，如果是无限个的话就变成了级数
• $\spadesuit$(p6:(5)7行)需要倒背如流，第七个用拉格朗日去证
• 拉格朗日的作用，导数为0和导数为正无穷，导数值决定了函数值(证明)
• $\bigstar$(真题) $\spadesuit$(p？:1.3.2 ) 排除法

局部保号性 $\bigstar$

如果 $\lim_{x \to x_0}f(x)=A,且$A>0$(或$A<0$),那么存在常数$\delta >0$,使得当$0< \lvert x - x_0 \rvert < \delta$是，有$f(x)>0$(或$f(x)<0$)

---

简单的证明

戴帽法 极具区分度，一定要记准确

运算法则

定理1 两个无穷小的和是无穷下

推广：有限个无穷小的和也是无穷小

定理2 有界函数与无穷小的乘积是无穷小

推论1 常数与无穷小的乘积是无穷小

推论2 有限个无穷小的乘积是无穷小

定理3 加减乘除的极限等于极限的加减乘除

如果 $\lim f(x)=A, \lim g(x)=B$那么

(1) $\lim \lbrack f(x) \pm g(x) \rbrack =\lim f(x) \pm \lim g(x)=A \pm B$

(2) $\lim \lbrack f(x) \cdot g(x) \rbrack =\lim f(x) \cdot \lim g(x)=A \cdot B$

(3) 若又有$B \neq 0,\text{则}$

$$\lim \dfrac{f(x)}{g(x)}= \dfrac{\lim f(x)}{\lim g(x)}= \dfrac{A}{B}$$

推论1 如果$\lim f(x)$存在，而$c$为常数，那么$\lim \lbrack cf(x) \rbrack = c\lim f(x)$

推论2 如果$\lim f(x)$存在，而$n$为正整数，那么$\lim \lbrack f(x) \rbrack^n = [\lim f(x)]^n$

定理6(复合函数的极限运算法则)

设函数$y=f\lbrack g(x) \rbrack$是由函数$u=g(x)$与函数$y=f(u)$复合而成,$f\lbrack g(x) \rbrack \text{在点}x0$的某去心领域内有定义，若$\displaystyle \lim{x \to x0}g(x)=u_0, \displaystyle \lim{u \to u_0}f(u)=A\text{,且存在}x \in \mathring{U}(x_0,\delta_0)\text{时,有}g(x) \neq u_0$则

$$\displaystyle \lim_{x \to x_0} f\lbrack g(x) \rbrack =\displaystyle \lim_{u \to u_0}f(u)=A$$

---

如果两个函数的极限存在，那么对应极限的加减乘除等于对饮加减乘除的极限

• 注意除法，分母不能是0

夹逼准则

• 既可以是一个数也可以是无穷大
• 夹逼准则很精彩
• $x-1<[x] \leq x$

洛必达法则

法则一

必须满足下面三个条件

两个函数都趋向于0

${\textstyle\unicode{x2460}}$ 两个函数可导

两个函数相除的极限存在，趋向于0或者无穷大

$$\text{则}\displaystyle \lim_{x \to \cdot} \dfrac{f(x)}{F(x)} \buildrel \rm \dfrac{0}{0} \text{或者} \dfrac{\infty}{\infty}\over{=} \displaystyle \lim_{x \to \cdot} \dfrac{f'(x)}{F'(x)}$$

第三点条件很重要，一个反例

右边存在左边必定存在，反之不然

常识性问题$\displaystyle \int_0^\pi sin(x)dx=2$

$$\displaystyle \lim_{x \to + \infty} \dfrac{\displaystyle \int_a^x |sin(x)|dt}{x} \buildrel \rm \dfrac{\infty}{\infty}\over{=}\displaystyle \lim_{x \to + \infty} \dfrac{|sin(x)|}{1}$$

但是洛必达失效$\mho$(涉及到的知识比较多，之后再讲)

泰勒公式 $\bigstar$ $\bigstar$ $\bigstar$

8个重要函数

公式

8个重要函数

$sin(x)$是奇函数，展开绝对没有偶函数

掌握无穷小的计算规则 $\spadesuit$(p38: 掌握无穷小的计算规则)

$\dfrac{A}{B}$ $\bigstar$(考研真题) $\spadesuit$(p36:考研真题)

展开原则

$A-B$型，展开至系数不相等的$k$次幂

常见的等价变化，$\spadesuit$(p38:常见的等价变化)

强调的两个等价变换

• $x + sin(x)\backsim 2x$
• $x - sin(x)\backsim \dfrac{1}{6}x^3$

归结原则(函数极限与数列极限的关系)

如果极限$\displaystyle \lim{x \to x_0}f(x)$存在,$\lbrace x_n \rbrace$为函数$f(x)$的定义域内任一收敛于$x_0$的数列，且满足:$x_n \neq x_0(n \in N+)$,那么相应的函数值数列$\lbrace f(xn) \rbrace$必收敛,且$\displaystyle \lim{n \to \infty}f(xn)=\displaystyle \lim{x \to x_0}f(x)$

---

海涅定理：联系离散和连续的常识

海涅定理只用不证

右推课本的例子

$\bigstar$(真题) $\spadesuit$(p？:例题1.3.14) 左推

• 幂值函数写成$u^v=e^{vlnu}$
• $ln(1+g(x)) \backsim g(x),g(x) \to 0$
  • $lnu = ln(1+u-1) \to u-1,u \to 1$

无穷小比阶(题型)

• 无穷大和极限都是一个过程
• 不是所有的无穷小都能比阶 $\mho$(反例，书本上的)

七种未定式的计算

$\dfrac{0}{0}\text{0比0} ,\quad$ $\dfrac{\infty}{\infty} \text{无穷比无穷},\quad$ $\infty \cdot 0\text{无穷乘0}$

$\infty - \infty\text{无穷减无穷}$,

$\infty^0\text{无穷的0次方}, \quad0^0\text{0的0次方}, \quad1^{\infty}\text{1的无穷次方}$

5种方法

• 四则运算方法
• 洛必达法则
• 泰勒公式
• 归结原则
• 夹逼准则

第一步：化简

• $e^{f(x)}-e^{g(x)}=e^{g(x)}[e^{f(x)-g(x)}-1] \backsim f(x)-g(x)$
• $e^{sin(x)}-e^{(x)}=sin(x)-x=-\dfrac{1}{6}x^3$

第二步判断类型：7种中的一种

$\dfrac{0}{0}$，$\dfrac{\infty}{\infty}$

• 洛必达
• 泰勒展开

$\spadesuit$(p？:例1.3.3)

• 上面次数高，地面次数低，方便运算
• 倒代换

$\spadesuit$(p？:例1.3.6)

• $\infty \cdot 0$
• $\sqrt{a}-\sqrt{b}$
• 注意负代换

$\bigstar$(题目的结论要记住) $\spadesuit$(p？:例1.3.7)

• 设置分母有原则，简单因式才下放
  • 简单：$x^\alpha ,x^{\beta x}$
  • 复杂：$ln(x),arcsin(x),arctan(x)$

$\spadesuit$(p?:例1.3.8) 泰勒展开

$\infty - \infty$

• 因式分解
• 通分（创造分母通分）
  • 转换成0/0
• 和差化积

$$\infty - \infty = \begin{cases} (1) & \text{有分母,则通分} \cr (2) & \text{没有分母，创造分母,再通分(倒代换)} \end{cases}$$

$\spadesuit$(p？:1.3.10 )

• 有分母则同分

$\spadesuit$(p？:例1.3.11)

• 没有分母，创造分母再通分
• $e^x-1-x \backsim \dfrac{1}{2}x^2(x \to 0)$

$\infty^0,0^0,1^{\infty}$

• 幂指函数

$\spadesuit$(p？:例1.3.12)

• $\infty^0$
• $\bigstar$(必考题) $(ln(x+\sqrt{1+x^2}))’=\dfrac{1}{\sqrt{1+x^2}}$

$\spadesuit$(p?:例1.3.13,例1.3.14 $1^\infty$)

• $lim u^v$ $\buildrel \rm \dfrac{1}{\infty}\over{=}$ $e^{lim v lnu}=e^{lim v(u-1)}$

连续与间断

• 是函数极限的应用
• 连续和间断是逐点的概念
• 考题只看两类点
  • 分段函数的分段点$\spadesuit$(p？:例1.3.20) $\spadesuit$(p？:例1.3.21)
  • $\bigstar$ 函数的无定义点$\spadesuit$(p？:例1.3.22)

$\spadesuit$(p？:例1.3.20)

连续点的定义

• 极限值=函数值，连续

间断点的定义与分类

设函数$f(x)$再点$x_0$的某去心领域内有定义(前提， 极限是一个过程)

• $\color{green}{\text{可去间断点}}$ 、 $\color{green}{\text{跳跃间断点}}$ 是 $\color{red}{\text{第一类间断点}}$
• $\color{green}{\text{无穷间断点}}$ 、 $\color{green}{\text{震荡间断点}}$ 是 $\color{red}{\text{第二类间断点}}$
• $\displaystyle \lim_{x \to 0^+ }xln(x)$
  • $\blacktriangleright$(明明求导的时候x趋向0的速度是1，lnx趋向0的速度是无穷大，为什么其极限还是0)

$\sharp$ 菲赫金哥尔茨微积分教程

可去间断点

也叫可补间断点
两种情况

• 若$\displaystyle \lim_{x\to x_0}f(x) = A \neq f(x_0)$
• $f(x)$无定义

跳跃间断点

极限有两个值，跳跃间断点

无穷间断点

$\displaystyle \lim_{x \to x_0}f(x) = \infty$

• 至少一个为无穷大

震荡间断点

$\displaystyle \lim_{x \to x_0}f(x)$ = 震荡不存在

• $\displaystyle \lim_{x \to x_0}sin \dfrac{1}{x}$

高等数学 ch4.一元函数微分学的概念与计算

• 知识结构：概念，计算，应用

$\mho$(函数可导,导函数必定连续？)

概念

引例

导数的概念

• $\displaystyle \lim_{x \to 0} \dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$
• 角点
• $f(x)=x^{\frac{1}{3}}$在$x=0$处的切线问题
  • 连续不一定可导

$\spadesuit$(p6:7个结论)

• $\spadesuit$(p60:例1.4.1)
  • 用定义
  • -0=+0

$\bigstar$(真题) $\spadesuit$(p61:例1.4.3)

$\bigstar$(真题) $(uv)’=u’v+uv’$

$\mho$(补充完过程)

$$\begin{split} (uv)' &=\displaystyle \lim_{\Delta x \to 0} \dfrac{f(x+\Delta x)-f(x)}{\Delta x} \cr &=\displaystyle \lim_{\Delta x \to 0} \dfrac{u(x+\Delta x)v(x+\Delta x)-u(x)v(x)}{\Delta x} \cr &= \end{split}$$

$\mho$(一点可导一点必连续)

$\flat$(定理证明) 猜题：费马定理，牛顿莱布尼茨公式

$\spadesuit$(p61:例1.4.3)

• $\mho$(重要材料)

错误的选项的方法：举反例

微分的概念

一元微积分一个东西在动，其他都不能动

• 增量$\Delta y=f(x_0+\Delta x)-f(x_0)=A\Delta x + o(\Delta x)$
• 线性主部(微分)+误差

$\spadesuit$(p?:例1.4.7)

导数与微分的计算

$\bigstar$(热点) $\spadesuit$(p62:例1.4.8)

tanx求导的推导

$\bigstar$(结论) $(ln(|x|))’=\dfrac{1}{x}$视绝对值而不见

• 导数除以其自己积分的原函数是$ln(u(x))$

$\spadesuit$(p?:例题1.4.10)

• 可导必连续，连续导数值等于函数值

双曲正弦，双曲余弦

$\spadesuit$(p:例1.4.13)

• 直接链式求导
• 先复合再求导

四则运算

分部积分：交换积分的位置

• $(uv)\prime=\dfrac{u\prime v-uv\prime}{v^2}$

分段函数的导数

• ${\textstyle\unicode{x2460}}$ 在分段点用导数定义法求导数是否存在
  • $\blacktriangleright$(为什么不能用求导公式)[难道是之前解释过的领域才有极限的概念]
• ${\textstyle\unicode{x2461}}$ 非分段点，用导数公式

复合函数的导数与微分形式不变性

• 微分形式不变 $df(\text{狗})=f’(\text{狗})d\text{狗}$
  • 二阶微分形式没有这个性质

反函数的导数

• $\varphi’(y)=\dfrac{1}{f’(x)},\varphi’’(y)=-\dfrac{f’’(x)}{ [ f’(x) ]^3 }$
• $\spadesuit$(p4:反函数) 有反函数的充分条件是单调
• $\spadesuit$(p91:例题1.6.8) $f’(x)$必保号
  • 达布定理(有正有负必有零点)
  • $\blacktriangleright$(？1.6.8导数零点定理和达布定理有关系吗)
• $\spadesuit$(p64:例1.4.15)
• $\clubsuit$ 变限积分函数 $\spadesuit$(p60:10)
  • $S’(x)=\displaystyle \int_{\varphi_1(x)}^{\varphi_2(x)}g(t)dt=g[\varphi_2(x)]\cdot \varphi_2’(x)-g[\varphi_1(x)]\cdot\varphi_1’(x)$
• $\sharp$
  • $dx\cdot dx=dx^2$ 叫微分的幂
  • $2xdx=d(x^2)$叫 幂的微分
  • p62
• $\bigtriangledown$ $yx’$指的是y对x求导，$y{xx}’’$指的是y对x求二阶导，$x_y’$指的是x对y求导
• $\mho$(反函数的工程意义)

参数方程所确定的函数的导数

• $\spadesuit$(p65:例1.4.17) 二阶导

隐函数求导法

$\bigstar$(一天不能停)

• 公式法
  • $F(x,y)=0$,$F’(x,y)=-\dfrac{F’x}{F’y}$
• 两边求导

$\bigstar$(使用性强) 对数求导法

图片详情

$\spadesuit$(p65:例1.4.19)

• $ln$加绝对值求导可以视绝对值不变

$\bigstar$(命题要素) 幂指函数求导法

例题1

例题2

• $\spadesuit$(p66:例题1.4.20)
  • $y=x^x$
  • $\mho$(画图) $xe^{\frac{1}{x}}$

高阶导数

归纳法

图片详情

$\spadesuit$(p66:例1.4.22)

• 直接归纳

$\spadesuit$(p67:例1.4.23)下面的框框

• 用诱导公式

莱布尼茨公式

图片详情

• 牛顿的二项展开

泰勒公式

• 零点展开叫麦克劳林公式
  • 非零点叫泰勒公式

变限积分求导公式

基本求导公式

公式	题目
$(x^a)\prime=ax^{a-1}\text{(a为常数)}$
$(a^x)\prime=a^xlna(a>0,a\neq 1)$
$(e^x)\prime=e^x$
$(log_ax)\prime=\dfrac{1}{xlna}(a>0,a\neq 1)$
$(ln x)\prime=\dfrac{1}{x}$
$(sin x)\prime=cos x$
$(cos x)\prime=-sin x$
$(arcsin x)\prime=\dfrac{1}{\sqrt{1-x^2}}$
$(arccos x)\prime=-\dfrac{1}{\sqrt{1-x^2}}$
$(tan x)\prime=sec^2x$	1
$(cot x)\prime=-csc^2x$
$(arctan x)\prime=\dfrac{1}{1+x^2}$
$(arccot x)\prime=-\dfrac{1}{1+x^2}$
$(sec x)\prime=sec x tan x$
$(csc x)\prime=-csc x cot x$
$[ln(x + \sqrt{x^2+1})]’=\dfrac{1}{\sqrt{x^2+1}}$
$[ln(x + \sqrt{x^2-1})]’=\dfrac{1}{\sqrt{x^2-1}}$

跟 $\color{red}{\text{cos}}$ 相似度高的都会出现 $\color{green}{\text{负号}}$

高等数学 ch5.一元函数微分学的几何应用

三点两性一线

• 三点
  • 极值点
  • 最值点
  • 拐点
• 两性
  • 单调性
  • 凹凸性
• 一线
  • 渐近线

$\spadesuit$(p80:例1.5.11) 有能力画图

极值与最值的概念

• 定义1，2
• 极值是局部的，最值是整体的
• 极值点双侧有定义
• $\spadesuit$(p72:举例子) 最值不到一定是极值，极值不一定是最值
• $\spadesuit$(p72:注三) 间断点可以是极值点

极值

最值

单调性与极值的判别

$\bigstar$(非常漂亮的考题) $\spadesuit$(p77:例1.5.1)(抽象函数)

• $\bigstar$*无数 $\spadesuit$(p86:定理7) 拉格朗日中值定理
• 补充的定理

$\spadesuit$(p77:例1.5.2)(显函数)留到 $\spadesuit$(p?:例题1.5.11)讲

$\spadesuit$(p？:例1.5.3) 隐函数
既然无穷阶可导，直接用定理2更快

$\spadesuit$(p？:例1.5.4) 隐函数

$\spadesuit$(p？:例1.5.6) 参数方程

基础班没有做题型的划分，强化班更为清晰的解题的思路和结构

单调性的判别

$f’(x)>0$则导数单调增

判别值的必要条件

费马定理($\spadesuit$(p?:第六讲证明))

• 一阶可导点是极值点的必要条件
• 是必要不是充要
  • $y=x^3,y’|{x=0}=3x^2|{x=0}=0$不是极值点

判别值的第一充分条件

$f(x)$在$x=x_0$处连续，且在$x_0$的某去心领域$\mathring{U}(x_0,\delta)$内可导
$\mho$(三点)

判别值的第二充分条件

可由判别值的第一充分条件推出

$\bigstar$(真题证明题的思路) 用局部保号性证明

判别值的第三充分条件

取n为2时,即为判别值的第二充分条件

$f(x)$在$x_0$处$n$阶可导，且$f^m(x_0)=0(m=1,2,\cdots,n-1),f^n(x_0) \neq 0(n \geq2)$，则

${\textstyle\unicode{x2460}}$当$n$为偶数且$f^n(x_0) < 0$时，f(x)在$x_0$处取得极大值

${\textstyle\unicode{x2461}}$当$n$为偶数且$f^n(x_0) > 0$时，f(x)在$x_0$处取得极小值

凹凸性与拐点的概念

凹凸性

比较函数值的中点和割线的中点

凹曲线$f(\dfrac{x_1+x_2}{2})<\dfrac{f(x_1)+f(x_2)}{2}$

凸曲线$f(\dfrac{x_1+x_2}{2})>\dfrac{f(x_1)+f(x_2)}{2}$

拐点

连续曲线的凹凸的分界点

注意两段表达

$$\begin{cases} \text{拐点在曲线上，写作}(x_0,f(x_0)) \cr \text{极值点在定义域上，写作}x_0 \end{cases}$$

凹凸性与拐点的判别

图片详情

$\bigstar$(训练解题能力) $\spadesuit$(p？:例1.5.5) 对比 $\spadesuit$(p？:例1.4.8)来看

$\spadesuit$(p？:例1.5.6)

凹凸性判别

判拐点的必要条件

二阶可导是拐点的必要条件

$\sharp$ 单纯->复杂(知道题目背后的陷阱和损招)->单纯

$\bigstar$(回顾) 一个幂函数

$$(x-x_0)^n = \begin{cases} \text{求n阶导} \implies n! \neq 0 & \cr \text{求n+1阶导} \implies 0& \end{cases}$$

判拐点的第一充分条件

判拐点的第二充分条件

判拐点的第三充分条件

渐近线

水平线和斜渐近线在一个方向上不会同时存在

$\spadesuit$(p？:1.5.7)

• 求渐近线的程序
  • ${\textstyle\unicode{x2460}}$ 先找无定义点$x0$，求$\displaystyle \lim{x \to x{0^+},x{0^-},x_{0}}f(x)$是否为$\infty$,若是$\infty$则为铅锤渐近线;
  • ${\textstyle\unicode{x2461}}$ 求$\displaystyle \lim_{x \to +\infty,-\infty,\infty}f(x)$是否存在为A，若为A则存在水平渐近线
  • ${\textstyle\unicode{x2462}}$ 求$\displaystyle \lim_{x \to +\infty,-\infty,\infty}f(x)=\infty$,求$k,b$，是否为非零常数，若是常数则为斜渐近线

铅锤渐近线

看函数的无定义点

水平渐近线

看正无穷和负无穷是否趋向于一个数

斜渐近线

$\displaystyle \lim_{x \to \infty}[f(x)-(kx+b)]=0$

${\textstyle\unicode{x2460}}$ $k= \displaystyle \lim_{x \to \infty}\dfrac{f(x)}{x}$

${\textstyle\unicode{x2461}}$ $b=\lim_{x \to \infty}[f(x)-kx]$

$y=x+sin(x)$没有斜渐近线

$y=x+sin(\dfrac{1}{x})$有斜渐近线$y=x$

$\sharp$ 斜渐近线必须是和x的同阶无穷大

最值或取值范围

是一个全局的概念所以放在最后讲

$\dagger$(1.5.10) 幂值函数

• $\displaystyle \lim_{x \to 0^+}\dfrac{ln(x)}{x},\dfrac{- \infty}{0}=0$
• $x^{\dfrac{1}{x}}$的图像
  • 

闭区间$[a,b]$

这些都是基本功，扎扎实实的做好

$$\text{比较得出最大和最小}\begin{cases} (可疑点)f'(x)= \begin{cases} =0 \cr 不存在 \end{cases} \cr \text{端点}a,b & \end{cases}$$

开区间$(a,b)$

$$\text{比较得出最大和最小}\begin{cases} (可疑点)f'(x)= \begin{cases} =0 \cr 不存在 \end{cases} \cr \displaystyle \lim_{x \to \star}f'(x)= \begin{cases} =A(\text{常数或}\infty)(\text{左}) \cr =B(\text{常数或}\infty)(\text{右}) \end{cases} \end{cases}$$

做函数图像

${\textstyle\unicode{x2460}}$ 先看性质看奇偶性

${\textstyle\unicode{x2461}}$ $f(x)$定义不存在的点,单调性，凹凸性，极值点拐点

$$f(x)=\text{不存在}$$ $$f'(x) = \begin{cases} 0 (\text{驻点}) \cr \text{不存在(不可导点)} & \end{cases}$$ $$f''(x) = \begin{cases} 0 (\text{拐点}) \cr \text{不存在(不可导点)} & \end{cases}$$

${\textstyle\unicode{x2462}}$ 确定渐近线

${\textstyle\unicode{x2463}}$ 做出函数图形

题目

$\bigstar$(题源 ) $\dagger$(1.5.11)

高等数学-ch6.十大定理及其使用

pp.92

十大定理及其使用

• 定理1-4为函数定理
• 定理5-9为导数定理
• 定理10为积分定理
• 对比着看
  • $\dagger$(1.6.1) 离散的平均值定理：平均值定理
  • $\dagger$(1.6.2) 连续的平均值定理：积分中值定理

$\sharp$ 讲课风格：概念-练习-总结（升华）

定理1：有界与最值定理

$m \leq f(x) \leq M$,其中$m$,$M$分别为$f(x)$在$[a,b]$上的最小值与最大值

$\color{green}{\text{意义：}}$ 函数一定在最大值和最小值之间

定理2：介值定理

当$m \leq \mu \leq M$时，存在$\xi \in [a,b]$,使得$f(\xi)=\mu$

---

$\color{green}{\text{意义：}}$ 如果一个数在最大值和最小值之间，位于 $\xi$ 处的点可以取到这个值

• 信号：看到区间给的是闭区间

定理3：平均值定理

当$a<x_1<x_2<\cdots<x_n<b$时，在$[x_1,x_n]$内至少存在一点$\xi$,使$f(\xi)=\dfrac{f(x_1)+f(x_2)+\cdots+f(x_n)}{n}$

---

$\color{green}{\text{意义：}}$ 位于 $\xi$ 处的点为所有数的平均值

• 证明
• 连续型和离散型两种考法
• 看到函数值加加加，就想到除以其个数
  • p93 习题1.6.2

$\bigstar$(真题，12年) $\dagger$(1.6.7)

定理4：零点定理

当$f(a)\cdot f(b)<0$时，存在$\xi \in(a,b)$,使得$f(\xi)=0$

---

$\color{green}{\text{意义：}}$ 函数出现正负变化，位于 $\xi$ 处的点，能取到0

• 由介值定理推出来

$\bigstar$(可能会考证明题) 定理5：费马定理

$$\text{设}f(x)\text{满足在}x_0\text{处}\begin{cases} {\textstyle\unicode{x2460}} \text{可导}, \cr {\textstyle\unicode{x2461}} \text{取极值}, \end{cases} \text{则}f'(x)=0$$

---

• $\bigstar$(${\textstyle\unicode{x2460}}$) 可导+极值(区间内部的最值) $\implies$ $f’(x_0)=0$
  • 一定要快，不要拖泥带水
• $\bigstar$(${\textstyle\unicode{x2461}}$)证明
  • 脱帽法值严格的不等
  • 戴帽法是非严格的不等
• $\bigstar$(${\textstyle\unicode{x2462}}$) $\dagger$(1.6.8)达布定理(也叫导数介值定理)
• ch5讲过
• 端点处无法用费马定理
• 费马定理的应用：当一个人跑到最远处时，他的速度为零;当一个人跑的最快的时候他的加速度为0

$\sharp$ 费马大定理 $x^n+y^n=z^n$大于2没有正整数解，经过300+年威尔斯证出来，为了证明这个创立了7门独立的学科

$\sharp$ 值得一看的书:《费马大定理》

$\bigstar$ 导数零点定理

$\bigstar$(特性)) 只要找到导数异号的两个点，中间一定有导数为0的点

• $\spadesuit$(p58:书页标签) 前面讲过的知识 $f’(x) \neq0 \implies f’(x)$保号
  • 单调函数必有反函数

$\spadesuit$(p90:1.6.8)

设$f(x)$在$[a,b]$上可导，证明当$f’+(a)\cdot f’-(b)<0$时，存在$\xi\in(a,b)$，使得

$$f'(\xi)=0$$

$\clubsuit$ 导数的定义

$\mho$(极限保号，脱帽戴帽法) $\blacktriangleright$(脱帽戴帽法的前提函数连续？)

定理6：罗尔定理

$$\text{设}f(x)\text{满足} \begin{cases} {\textstyle\unicode{x2460}} \text{在}[a,b]上连续, \cr {\textstyle\unicode{x2461}} \text{在}(a,b)\text{内可导，则存在} \xi \in (a,b),\text{使得}f'(\xi)=0\cr {\textstyle\unicode{x2462}} f(a)=f(b), \end{cases}$$

---

• $f(x)=0$有两个根$\implies$ $f’(x)$至少有一个根
• 抓住两个问题：${\textstyle\unicode{x2460}}$找端点值相同，${\textstyle\unicode{x2461}}$找谁($F(x)$)的端点值相同
  • $\spadesuit$(p89:如何构造辅助函数)
    • 逆用乘积求导公式
      • $\dagger$(1.6.4) $f(x)f’(x) \implies F(x)=f^2(x)$
      • $[f’(x)]^2 \implies F(x)=f(x)f’’(x)$
      • $[f’(x) + f(x)\varphi’(x)]e^{\varphi(x)} \implies F(x)=f(x)e^{\varphi(x)}$

费马定理关键是找极值，罗尔定理找端点值相同，都能推出$f’(\xi)=0$

罗尔vs拉格朗日：罗尔证明导数为0，拉格朗日得到导数为一个数，拉格朗日可以推罗尔：斜线变直

zy觉得很显然？没怎么看懂
$\dagger$(1.6.5) $f’(\xi)+df(\xi)=0$

$\dagger$(1.6.6) $f’(\xi)-\lambda[f(\xi)-\xi]=1$

• $\bigstar$(标准题)第二问遇到了困难，第一问是锦囊

$\dagger$(1.6.7) 两次罗尔定理

• $\bigstar$(把罗尔定理用到了极致)
• 
• 可以直接用积分中值定理证明(必须用注里面的方法，因为原定理是闭区间)

证明题见到积分的思路

$$\text{证明题，见到} \int_a^bf(x)dx= \begin{cases} {\textstyle\unicode{x2460}} \text{积分中值定理} f(\xi)(b-a) & \cr {\textstyle\unicode{x2461}} \text{令} F(x)=\int_a^xf(t)dt& \end{cases}$$

$\sharp$ $\blacktriangleright$(什么是解题技巧，什么是基本东西) 不能光讲解题技巧忽略了基本的东西，(考题第一题，证明费马定理完了)

$\dagger$(习题1.6.3)$f’(\xi)=(1-\dfrac{1}{3})f(\xi)$

定理7：拉格朗日中值定理

$$\text{设}f(x)\text{满足} \begin{cases} {\textstyle\unicode{x2460}} \text{在}[a,b]上连续, \cr {\textstyle\unicode{x2461}} \text{在}(a,b)\text{内可导} \end{cases} \text{使得}$$ $$f(b)-f(a)=f'(\xi)(b-a)$$ $$\text{或者写成}$$ $$f'(\xi)=\dfrac{f(b)-f(a)}{b-a}$$

---

• 几何意义：割线与切线平行
• 作用上：$f(b)-f(a)=f’(\xi)(b-a)$
• 常用的:$f(x)-f(x_0)=f’(\xi)(x-x_0)$
• 见到$f-f$想到拉格朗日
  • $e^x-1=e^x-e^0=e^\xi\cdot x$
• 联系f与$f’$, 立刻想到拉格朗日

$\dagger$(1.6.9)

$\dagger$(1.6.11)

• 用一次拉格朗日是小题
• 此题用两次是大题
• 不同的两个数要用$\tau$将区间切分

$\flat$(思路预测)

$$\begin{cases} {\textstyle\unicode{x2460}} \text{方向：}\text{ 思路(考研)(smart 巧)} \begin{cases} \cancel{\text{易}}\text{只在一个点上刷题没有意义} \cr \cancel{\text{难}}\text{中规中矩} \end{cases} \cr {\textstyle\unicode{x2461}} \text{做题：} \text{做题的数量(但也不用太多，思路正确的题目)} \uparrow \end{cases}$$

定理8：柯西中值定理

$$\text{设}f(x),g(x)\text{满足} \begin{cases} {\textstyle\unicode{x2460}} \text{在}[a,b]上连续, \cr {\textstyle\unicode{x2461}} \text{在}(a,b)\text{内可导,则存在}\xi \in(a,b),\text{使得} \cr {\textstyle\unicode{x2462}} g'(x) \neq 0 \end{cases}$$ $$\dfrac{f(b)-f(a)}{g(b)-g(a)} = \dfrac{f'(\xi)}{g'(\xi)}$$

---

• ${\textstyle\unicode{x2460}}$ 两次拉格朗日相除证柯西是错误的
  • 不知道两个$\xi$是否相等
• ${\textstyle\unicode{x2461}}$ 取$g(x)=x$拉格朗日是柯西的特例
  • 柯$\implies$拉$\implies$罗尔
• ${\textstyle\unicode{x2462}}$ ${\textstyle\unicode{x2462}}$ 怎么考
  • 一个抽象($f(x)$),一个具体($g(x)$)
  • $\dagger$(1.6.12)

一个数不为零往往是在分母上

证明$g’(x) \neq 0$一般用反证法

$\bigstar$(热点，极为重要) 定理9：泰勒公式

$\bigstar$(真题) $\dagger$(1.6.13)

• $\xi$是端点的函数不能往外面提
• $f(x)\leftrightarrowd f(x) \leftrightarrow f’(x) \leftrightarrow f’’(x)$
  • 
• 总结上面习题得到的知识结构：$\dagger$(1.6.3)
• 
• 习题1.6.5 导数介值定理也是用费马定理证
  • 在区间内可导就可以取这个区间内的所有值(要么连续，要么震荡间断点)

带拉格朗日余项的n阶泰勒公式

设$f(x)$在点$x_0$的某个领域内$n+1$阶导数存在，则对该领域内的任意点$x$,有

$f(x)=f(x_0)+f’(x_0)(x-x_0)+\cdots+\dfrac{1}{n!}f^{(n)}(x_0)(x-x_0)^n+\dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}$

其中$\xi$介于$x,x_0$之间

---

• 最高导数是几就念几阶
• $x_0=0$是麦克劳林展开
  • $\spadesuit$(p87:注2几个重要函数的麦克劳林展开)
  • $\spadesuit$(p73:4) 用二阶配亚诺余项的麦克劳林展开证明
• 在一个区间处的

带配亚诺余项的n阶泰勒公式

设$f(x)$在点$x_0$处n阶可导，则存在$x_0$的一个领域，对于该领域内的任意点，有

$f(x)=f(x_0)+f’(x_0)(x-x_0)+\dfrac{1}{2!}f’’(x_0)(x-x_0)^2+\cdots+\dfrac{1}{n!}f^{(n)}(x_0)(x-x_0)^n+o((x-x_0)^n)$

---

• 在一个点处的，局部的，极限的计算题

定理10：积分中值定理

设$f(x)$在$[a,b]$上连续，存在$\xi \in [a,b]$,使得

$$\int_a^bf(x)dx=f(\xi)(b-a)$$

---

• $\spadesuit$(p143:注3)

高等数学-ch7 零点问题与微分不等式

零点问题与微分不等式

• 零点问题也叫方程的根的问题

$\sharp$ 讲课风格：概念-练习-总结（升华）

$\sharp$ 做考卷高级境界：评价考题的好坏

• 怎么出的
• 还能怎么出

零点问题

• 有难度的是含参数的问题
  • $\dagger$(1.7.4) 和 $\dagger$(1.7.6)
    • 导数中不含参，在结果中讨论参数(曲线随着参数上下移动)
  • $\dagger$(1.7.7)
    • 导数中含参，过程中讨论参数，结果中不需要讨论

零点定理(证存在性)

设$f(x)$在$[a,b]$上连续，且$f(a)f(b)<b$,则$f(x)=0$在$(a,b)$内至少有一个根

• $[\text{注}]$推广的罗尔定理：若$f(x)$在$(a,b)$内连续，$\displaystyle \lim{x \to a^+}f(x)=\alpha$,$\displaystyle \lim{x \to b^-}f(x)=\beta$，且$\alpha \cdot \beta < 0$,则$f(x)=0$在$(a,b)$内至少有一个根，这里$a,b,\alpha,\beta$可以是有限数，也可以是无穷大

单调性(证唯一性)

若$f(x)$在$(a,b)$内单调，则$f(x)=0$在$(a,b)$内至多有一个根，这里$a,b$可以是有限数，也可以是无穷大

• 单调性的判断$f’(x)$存在且$\neq$ 0

罗尔原话

若$f^{n}(x)=0$至多有$k$个根，则$f(x)=0$至多有$k+n$个根

• 生活语言中的有两个是数学语言的有且仅有两个，数学语言的有两个是指至少有两个
• 此定理一般出选择题
• $\dagger$(1.7.2)

实系数奇次方程至少有一个根

$\dagger$(1.7.3)

微分不等式

$\dagger$(1.7.8)

• 主流：证明函数的单调性，然后比较大小

$\dagger$(1.7.9)

• 用了凹凸性

$\dagger$(1.7.10)

• $f’(x)=0,f^{\prime \prime}>0 \implies \text{极小值点}$ $\mho$(这个之前讲过，但是去查笔记没有查到)

$\dagger$(1.7.13)

$\bigstar$(结论特别重要) $\dagger$(1.7.14)

用函数性态证明不等式

性态指(单调性，凹凸性，最值)

若有$f’(x) \geq 0,a<x<b$, 则有$f(a) \leq f(x) \leq f(b)$

若有 $f^{\prime\prime}(x) \geq 0,a<x<b$，则有$f^{\prime}(a) \leq f’(x) \leq f’(b)$

${\textstyle\unicode{x2460}}$ 当$f’(a)>0$时，$f’(x)>0 \implies f(x)$单调增加

${\textstyle\unicode{x2461}}$ 当$f’(b) <0$时,$f’(x) < 0 \implies f(x)$单调减少

设$f(x)$在$I$内连续，且有唯一的极值点$x_0$,则

$$\begin{cases} \text{当}x_0 \text{为极大值时} f(x_0) \geq f(x) \cr \text{当}x_0 \text{为极大值时} f(x_0)\geq f(x)& \end{cases} \forall x \in I$$

若有$f^{\prime\prime}(x)>0,a<x<b,f(a)=f(b)=0$,则有$f(x)<0$

$\blacktriangleright$(？去查了ch5的笔记没有看到二阶导数与凹凸性的关系，确实是有讲过，但是没有记下来) 二阶导数有凹凸性

用常数变化量证明不等式

如果欲证的不等式中都是常数，则可以将其中一个或者几个常数变量化，再利用上面所述的导数工具去证明

用中值定理证明不等式

主要用拉格朗日中值定理或者泰勒公式

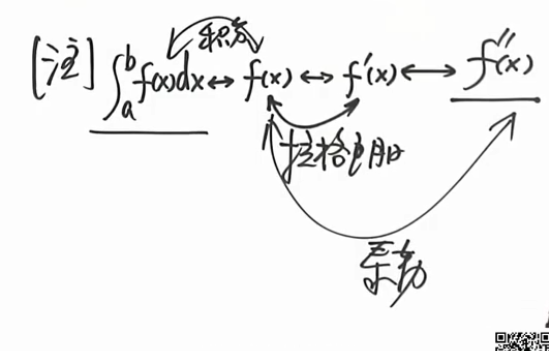
一元函数积分学的概念与计算

02是第二个视频t是时间

• 祖孙三代:积分，原函数，导数
  • $\int_a^x e^{t^2}dt \leftarrow e^{x^2} \rightarrow e^{x^2} \cdot 2x$
  • 考研常考：$\int_0^x e^{t^2}dt$,0做下限，按照函数奇偶性(todo)，原函数是偶函数只有其0下限的变限积分是奇函数,证明($\dagger$(1.8.6))
  • $\flat$(02 t=00:35:37.362) 周期性

2021.4.30 后面傅里叶的时候讲到$int_a^x f(x)dt$ 就不带常数没听懂

概念

不定积分

原函数与不定积分

设函数$f(x)$定义在某区间$I$上,若存在可导函数$F(x)$，对于该区间上任意一点都有$F’(x)=f(x)$成立，则称 $F(x)$是$f(x)$在区间$I$上的一个原函数,称$\int f(x)dx=F(x)+C$为$f(x)$在区间$I$上的不定积分,$C$为任意常数

原函数存在定理

(1) 连续函数$f(x)$必有原函数$F(x)$

(2) 含有第一类间断点、无穷间断点的函数$f(x)$在包含该间断点的区间内必没有原函数$F(x)$

• 含有震荡间断点的函数有原函数
• 导数介值定理可证
• $\bigstar$(结构性知识总结) 考研中的五种点
  • 连续点
  • 跳跃点
  • 可去间断点
  • 无穷间断点
  • 震荡点

定积分

• 定积分是个数,变限积分是函数

定积分的概念

$$\int_a^b f(x)dx=\displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=1}^nf(a+\dfrac{b-a}{n}i)\dfrac{b-a}{n}$$ $$\spadesuit\text{(p125:重点)} \text{取}a=0,b=1,\displaystyle \lim_{n \to \infty} \sum_{i=1}^nf(\dfrac{i}{n})\dfrac{1}{n}=\int_0^1f(x)dx$$

• 用定积分的定义解决题目的方法
  • ${\textstyle\unicode{x2460}}$ 先提出$\dfrac{1}{n}$
  • ${\textstyle\unicode{x2461}}$凑出$\dfrac{i}{n}$
  • 写出$\int_0^1f(x)dx$

$\bigstar$(结构性知识总结)基础30讲学基本的方法，推导，强化训练解决怪物的各种变形和形式，基础班相当于塞尔达的普通模式，强化班相当于塞尔达的大师模式(题目综合性强(怪物的组合更加综合)，血量变厚(综合，复杂))

定积分存在定理

$\blacktriangleright$(这些充分条件是交的关系还是并的关系:2021.4.30感觉是并的关系，充分条件本身就是小范围的条件，每一个点的则也能够看出来)

(1) 定积分存在的充分条件

${\textstyle\unicode{x2460}} \text{若} f(x)\text{在}[a,b]\text{上连续,则}\int_a^b f(x)dx\text{存在}$

${\textstyle\unicode{x2461}} \text{若} f(x)\text{在}[a,b]\text{上单调,则}\int_a^b f(x)dx\text{存在}$

${\textstyle\unicode{x2462}} \text{若} f(x)\text{在}[a,b]\text{上有界,且只有有限个间断点,则}\int_a^b f(x)dx\text{存在}$

(2) 定积分存在的必要条件

可积函数必有界，即若定积分$\int_a^b$ 存在,则$f(x)\text{在}[a,b]\text{上必有界}$

定积分的性质

假设积分均存在

性质1(求区间长度)

$\text{假设}a<b,\text{则}\int_a^bdx=b-a=L,\text{其中}L\text{为}\text{区间}[a,b]\text{的长度}$

性质2(积分的线性性质)

$\text{设}k_1,k_2\text{为常数,则}\int_a^b[k_1f(x) \pm k_2g(x)]dx=k_1\int_a^bf(x)dx\pm k_2\int_a^b g(x)dx$

性质3(积分的可加(拆)性)

$\text{无论}a,b,c\text{的大小如何,总有}\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx$

性质4(积分的保号性)

$\text{若在区间}[a,b]\text{上}f(x)\leq g(x)\text{,则有}\int_a^bf(x)dx\leq \int_a^bg(x)dx$

特殊地，有$|\int_a^bf(x)dx|\leq\int_a^b|f(x)|dx$(积分的绝对值小于等于绝对值的积分)

性质5(估值定理)

$\text{设}M,m\text{分别是}f(x)\text{在}[a,b]\text{上的最大值和最小值，}L\text{为区间}[a,b]\text{的长度,则有}mL\leq\int_a^bf(x)dx\leq ML$

$\bigstar$ $\bigstar$ $\bigstar$ 性质6(中值定理) $\text{设}f(x)\text{在闭区间}[a,b]\text{上连续，则在}[a,b]\text{上至少存在一点}\xi\text{,使得}\int_a^bf(x)dx=f(\xi)(b-a)$

• 拉格朗日证:令$F(x)=\int_a^xf(t)dt$

变限积分

变限积分的概念

• 变限积分就是定积分的推广
• 变限积分 $\int_a^xf(t)dt=F(x)$,$F(x)\text{就是}f(t)\text{的一个原函数}$(证明)

变限积分的性质

(1) $\text{函数}f(x)\text{在}[a,b]\text{上可积,则函数}F(x)=\int_a^xf(x)dx\text{在}[a,b]上连续$

(2) $\text{函数}f(x)\text{在}[a,b]\text{上连续,则函数}F(x)=\int_a^xf(x)dx\text{在}[a,b]上可导$

只要变限积分存在，变限积分就必定是连续的

如果函数$f(x)\text{在}[a,b]\text{上连续，则函数}F(x)=\int_a^xf(t)dt\text{在}[a,b]\text{上可导,且}F\prime(x)=f(x)$(证明)

变限积分的求导公式

$$F\prime(x)=\dfrac{d}{dx}[\int_{\varphi_1(x)}^{\varphi_2(x)}f(t)dt] = f[\varphi_2(x)]\varphi\prime_2(x) - f[\varphi_1(x)]\varphi\prime_1(x)$$

【注】︰我们称上面公式中的x为“求导变量”,t为“积分变量”.“求导变量”x只出现在积分的上、下限时才能使用变限积分求导公式,若“求导变量”x出现在被积函数中,必须通过恒等变形(比如变量代换等),将其移出被积函数,才能使用变限积分求导公式.

反常积分

• 区间长度无限
• 或者有无穷大的值

反常积分概念的通俗理解

• 将b和$\infty$带到积分上去算，算出来收敛，算不出来发散

$\mho$(例子的求和极限没看懂)

$$\int_a^{+\infty}f(x)dx\text{收敛不一定能推出}\displaystyle \lim_{x \to +\infty}=0$$

(上限无穷大的变限积分收敛不代表原函数趋于无穷的极限为0)

无穷区间上反常积分的概念与敛散性

• 在反常积分中，一般把“$\infty$”和使得函数极限为无穷的点(瑕点)统称为奇点.

无界函数的反常积分的概念与敛散性

如果函数f(x)在点a的一个邻域内无界，那么点a称为函数f(x)的 $\color{green}{\text{瑕点}}$

判敛

$\bigstar$ 计算

• $\bigstar$(知识结构)考研数学三大计算
  • 极限
  • 求导
  • 求积

基本积分公式

• 换元三换
  • 积分元素
  • 积分上下限
  • 被积函数

凑微分法

(1) 基本思想 $\int f[g(x)]g’(x)dx=\int f[g(x)]dg(x)=\int f(u)du$

也叫第一类换元法

• 题目：(1，2)

换元法

(1) 基本思想 $\int f[g(x)]g’(x)dx=\int f[g(x)]dg(x)=\int f(u)du$

• 举重若轻
• 倒代换，高次放上面，不稳定容易动
  • 倒代换的适用范围

(2)思维结构

• $\mho$(记得讲过换元法的技巧，比如见到x^2怎么换元什么的，补充一下)

  分部积分法

  (1) 基本思想 $\int udv=uv-\int vdu$
• 积分简单当v，求导简单那当u
• 反对幂指三(越左越$u$，越右越$v$)
  • v被积分，u被求导
  • 这个顺序刚好对应表格法的上下顺序，越左越上，越右越下

$\sharp$ 自己简化课本的知识让自己理解

$\spadesuit$(p112:注) 分部积分的推广公式，分部积分表格

有理函数积分

$\bigstar$(考前可能会忘掉)

直接用特殊值法求值

定积分的计算

用牛顿莱布尼茨公式，能带值代值，不能带值取极限

如果是找原函数的话，就是在考不定积分的能力，反之研究性质 $\spadesuit$(p114:注)

• 注4重点：区间在重现公式(别样换元法)
  • $f(x)+f(a+b-x)$
• 注5年年考：点火公式
  • 
  • 
  • 三个重要的结论

定积分的换元积分法

定积分的分部积分法

基本积分表

公式	题目
$\int x^kdx=\dfrac{1}{k+1}x^{k+1}+C,k\neq-1$
$\int \dfrac{1}{x^2}dx=-\dfrac{1}{x}+C$
$\int \dfrac{1}{\sqrt{x}}dx=2\sqrt{x}+C$
$\int \dfrac{1}{x}dx=ln\lvert x\rvert+C$
$\int e^xdx=e^x+C$
$\int a^xdx=\dfrac{a^x}{ln a}+C,(a >0 \text{且} a \neq 1)$
$\int e^xdx=e^x+C$
$\int sinxdx=-cosx+C$
$\int cos xdx=sin x+C$
$\int tan xdx=-ln\lvert cos x \rvert+C$
$\int cot xdx=ln\lvert sin x \rvert+C$
$\int\dfrac{dx}{cosx}=\int secxdx=ln\lvert secx+tanx \rvert+C$	1
$\int\dfrac{dx}{sinx}=\int cscxdx=ln\lvert cscx-cotx \rvert+C$
$\int sec^2xdx=tanx+C$
$\int csc^2xdx=-cotx+C$
$\int secxtanxdx=secx+C$
$\int cscxcotxdx=-cscx+C$
$\int \dfrac{1}{1+x^2}dx=arctanx+C$
$\int \dfrac{1}{a^2+x^2}dx=\dfrac{1}{a}arctan\dfrac{x}{a}+C$
$\int\dfrac{1}{\sqrt{1-x^2}}dx=arcsinx+C$
$\int\dfrac{1}{\sqrt{a^2-x^2}}dx=arcsin\dfrac{2}{a}+C$
$\int\dfrac{1}{\sqrt{x^2+a^2}}dx=ln(x+\sqrt{x^2+a^2})+C(\text{常见}a=1)$
$\int\dfrac{1}{\sqrt{x^2-a^2}}dx=ln\lvert x+\sqrt{x^2+a^2} \rvert+C(\lvert x\rvert>\lvert a \rvert)$
$\int\dfrac{1}{x^2-a^2}dx=\dfrac{1}{2a}ln\lvert \dfrac{x-a}{x+a} \rvert+C(\int \dfrac{1}{a^2-x^2}dx=\dfrac{1}{2a}ln\dfrac{\lvert x+a \rvert}{\lvert x-a \rvert}+C)$
$\int\sqrt{a^2-x^2}dx=\dfrac{a^2}{2}arcsin\dfrac{x}{a}+\dfrac{x}{2}\sqrt{a^2-x^2}+C$
$\int sin^2xdx=\dfrac{x}{2}-\dfrac{sin 2x}{4}+C(sin^2x=\dfrac{1-cos2x}{2})$
$\int sin^2xdx=\dfrac{x}{2}+\dfrac{sin 2x}{4}+C(cos^2x=\dfrac{1+cos2x}{2})$
$\int tan^2xdx=tanx-x+C(tan^2x=sec^2x-1)$
$\int cot^2xdx=-cotx-x+C(cot^2x=csc^2x-1)$

$\mho$(华理士公式(点火公式)也要补充在这里面)

$${\textstyle\unicode{x2461}} \int\dfrac{1}{x}dx=ln|x|+C$$

• 题目：(1)

$${\textstyle\unicode{x2465}} \begin{cases} \int \dfrac{1}{\sqrt{1-x^2}}dx = arcsin x + C , & \cr \int \dfrac{1}{\sqrt{a-x^2}}dx = arcsin \dfrac{x}{a} + C(a>0) . & \end{cases}$$

• 题目：(1，)

$${\textstyle\unicode{x2468}} \int\sqrt{a^2-x^2}dx=\dfrac{a^2}{2}arcsin\dfrac{x}{a}+\dfrac{x}{2}\sqrt{a^2-x^2}+C$$

• 题目：(1:推导)

一元函数积分学的几何应用

• 知识结构导学的时候提出一共7个考点
• 核心思想微元法
• 知识结构
  • 直角坐标系
  • 参数方程
  • 极坐标系

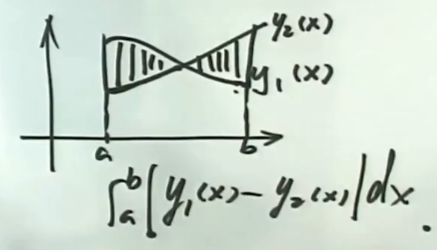
平面图形的面积

(1) 曲线$y=y_1(x)\text{与}y=y_2(x)\text{及}x=a,x=b(a < b)$所围成的平面图形的面积

$$S=\int_a^b |y_1(x)-y_2(x)|dx$$

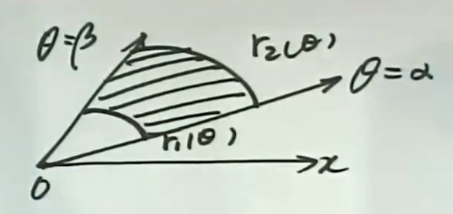
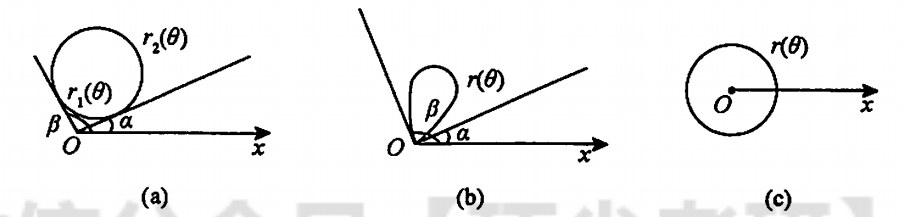
(2) 曲线$r=r_1(\theta)\text{与}r=r_2(\theta)\text{与两射线}\theta=\alpha\text{与}\theta=\beta(0 < \beta - \alpha \leq 2\pi)$所围成的曲边扇形的面积

$$S = \dfrac{1}{2}\int_\alpha^\beta|r_1^2(\theta)-r_2^2(\theta)|d\theta$$

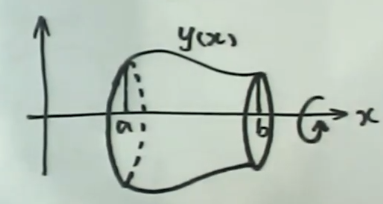
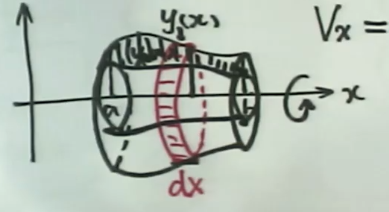
旋转体的体积

(2)曲线$y=y(x)\text{与}x=a,x=b(a<b)\text{及}x$轴围成的曲边梯形绕x轴旋转一周得到旋转体的体积

$$V=\int_a^b\pi y^2(x)dx$$

(2)曲线$y=y_1(x) \geq 0\text{与}y=y_2(x) \geq 0 \text{及}x=a,x=b(a < b)\text{所围成的平面图形绕}x$轴旋转一周所得到的旋转体的体积

$$V=\pi \int_a^b|y_1^2(x)-y_2^2(x)|dx$$

(3) 曲线$y=y(x)\text{与}x=a,x=b(0 \leq a < b)\text{及}x\text{轴围成的平面图形绕}y$轴旋转一周所得到的旋转体的体积

$$V_y=2\pi \int_a^bx|y(x)|dx$$

(4) 曲线$y=y_1(x)\text{与}y=y_2(x)\text{及}x=a,x=b(0\leq a \leq b)$所围成的图形绕$y$轴旋转一周所得到的旋转体的体积

$$V=2\pi\int_a^bx|y_1(x)-y_2(x)|dx$$

$\bigstar$ 函数的平均值

$\text{设}x\in[a,b],\text{函数}y(x)\text{在}[a,b]\text{上的平均值为}\bar{y}=\dfrac{1}{b-a}\int_a^by(x)dx$

$\bigstar$ 积分等式与积分不等式

• ch6 + ch10 是完整的中值定理问题

积分等式

用中值定理

用夹逼准则

• 信号:看到$\displaystyle \lim_{n \to \infty}\int_a^b$求极限的肯定是夹逼准则(算不出来才取极限)
• 记住一定是先积分再求极限

用积分法

积分不等式

用函数单调性

• 适用于$f(x)$连续的情况(必然有爸)

用拉格朗日中值定理

• 一般用于一阶导数
• $\bigstar$(注)可导必连续指的是函数可导函数必连续，导完之后不一定连续

用泰勒公式

• 一般用于二阶导以上

用积分法

多元函数微分学

基本概念

• $\clubsuit$ 一般考5分

平面点集的基本概念

• 不会考题
• $\mho$(面积分的时候还有别的概念)
• 聚点：里面的点和边界的点

极限

连续

不连续就不连续，不存在跳跃间断点之类的

$\bigstar$ $\bigstar$ $\bigstar$ 偏导数

可微

• 全微分:$y\Delta x+x\Delta y$
• 全增量:$\Delta z = A\Delta x+B\Delta o(\rho) = \dfrac{\partial z}{\partial x}\Delta x+ \dfrac{ \partial z}{\partial y}\Delta y= \dfrac{\partial z}{\partial x}d x+ \dfrac{ \partial z}{\partial y}d y$

$\mho$(p161) 判断函数一点是否可微的步骤

偏导数的连续性

$\mho$(p161) 判断函数一点是否连续的步骤

多元函数微分法则

• 计算10分-11分

链式求导法则

图片详情

• 一般是对显函数来讲
• 复合结构图
  • 就像走路一样
• 如果具有二阶连续偏导数，那么交换求偏导次序并不影响

隐函数存在定理(公式法)

• $\dfrac{dy}{dx} = - \dfrac{F_x’}{F_y’}$
• 全导数
  • 只有一个自变量，中间有中间变量，用最初的因变量与最终的自变量求导
• 分母不能为0
• 记忆方法：上下交换，填负号
• 一般来说显函数用链式，隐函数用公式(或者全微分不变性)
• x，y，z相当于中间变量是独立的

多元函数的极值与最值

• $\bigstar$(重要考点)

概念

无条件极值

(1) 二元函数取极值的必要条件(类比一元函数)

(2) 二元函数取极值的充分条件

• 原理：需要知道二次型的正定问题($\mho$(原理 ))

无条件极值的例题

隐函数

显函数

条件极值与拉格朗日乘数法

• 计算不出来的时候可以猜答案

图片详情

例题

• 2021真题
• 多元函数微分学条件极值(拉格朗日乘数法)求解技巧总结
• ~~二元函数构造只需 $\lambda$ ,三元函数构造需要 $\lambda$ 和 $\mu$ ~~，约束条件有多少个，就加多少个系数

闭区域边界上的最值

闭区域上的最值

二重积分

• 分值分布
• 5分+11分大题

概念、性质与对称性

几何背景

性质

性质1(求区域面积)

性质2(可积函数必有界)

性质3(积分的线性性质)

性质4(积分的可加性)

性质5(积分的保号性)

性质6(二重积分的估值定理)

性质7(二重积分的中值定理)

$\bigstar$(5分) 对称性

普通对称性

图片详情

轮换对称性

图片详情

• $x$和$y$对调之后，区域D不变
• 积分值与字母无关(谁动了我的面包)
• 轮换是指字母对换，对称是指区域不变
• 直角坐标系才能用

计算

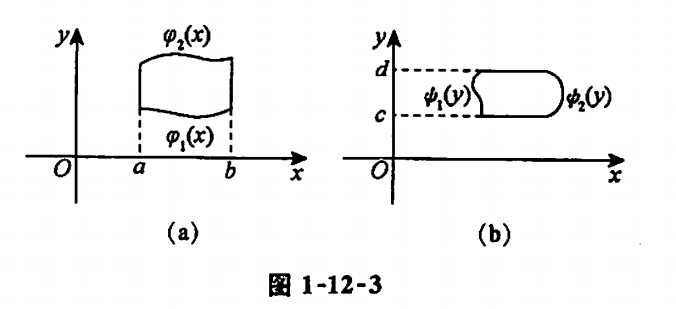
直角坐标系

后积先定限,限内画条线,先交写下限，后交写上限

(1) X型区域(上下型)(a图)

• 可以理解为限内的线在X轴上运动，所以叫X型区域,后积X

$$\displaystyle \iint_Df(x,y)d\sigma = \int_a^bdx\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy,\text{其中}D\text{为}X\text{型区域:}\varphi_1(x)\leq y\leq\varphi_2(x),a\leq x\leq b$$

(2) Y型区域(左右型)(b图)

• 可以理解为限内的线在Y轴上运动，所以叫Y型区域,后积Y

$$\displaystyle \iint_Df(x,y)d\sigma = \int_c^ddx\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)dx,\text{其中}D\text{为}Y\text{型区域:}\psi_1(y)\leq x\leq\psi_2(y),c\leq y\leq d$$

极坐标系

(1)极点O在区域D外部(a图)

$$\displaystyle \iint_Df(x,y)d\sigma = \int_\alpha^\beta d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(rcos\theta,rsin\theta)rdr$$

(2)极点О在区域D边界上(b图)

$$\displaystyle \iint_Df(x,y)d\sigma = \int_\alpha^\beta d\theta\int_0^{r(\theta)}f(rcos\theta,rsin\theta)rdr$$

(3)极点O在区域D内部(c图)

$$\displaystyle \iint_Df(x,y)d\sigma = \int_0^{2\pi}d\theta\int_0^{r(\theta)}f(rcos\theta,rsin\theta)rdr$$

在极坐标系下,几乎所有的计算都是先积$r$,后积$\theta$,所以一般不讨论积分次序的交换问题

极坐标系与直角坐标系的选择的一般原则

• ${\textstyle\unicode{x2460}}$ 看被积函数的形式:$f(x^2+y^2),f(\dfrac{y}{x}),f(\dfrac{x}{y})$
• ${\textstyle\unicode{x2461}}$ 积分区域是否是圆(主要看 ${\textstyle\unicode{x2460}}$ )

极直互化

• 极坐标系和极坐标系的互换
• 上下限反解xy

$$\begin{cases} x=r cos\theta , & \cr y=r sin\theta , & \end{cases}$$

积分次序

• 先积分x还是y

用二重积分处理一元积分的问题

• 特色

常微分方程

pp.191

可以看作是微积分的应用

$\bigstar$(反复多次看)

常微分方程的概念

用概念解题(5分)

• 例题1.13.11(考纲没有明确提，但是考研题里面有)
• 习题1.13.7(由微分方程,隐含了y任意阶可导)
  • 洛必达能不能用，用了再说？。？

解题过程中，解完之后校验答案是否正确

微分方程

含有 $\color{green}{\text{未知函数}}$ 及其 $\color{green}{\text{导数}}$ (或者微分)的方程称为微分方程,一般写成

$$F(x,y,y\prime,\cdots,y^{(n)})=0\text{或}y^{(n)}=f(x,y,y\prime,\cdots,y^{n-1})$$

最高阶导数不能缺

偏微分方程见上一讲的笔记

常微分方程

未知函数是 $\color{green}{\text{一元函数}}$ 的微分方程称为常微分方程，如$y\prime\prime\prime-y\prime\prime+6y=0,ydx-(x+\sqrt{x^2+y^2})dy=0$

微分方程的阶

方程中未知函数 $\color{green}{\text{导数的最高阶数}}$ 称为微分方程的阶,如:$y\prime\prime\prime-y\prime\prime+6y=0$就是三阶微分方程

微分方程的解

将函数带入微分方程，使方程称为恒等式，则该函数称为微分方程的解

微分方程的解是一个函数

微分方程的通解

• $\bigstar$(考研要求)
• 微分方程的解中含有的独立常数的个数等于微分方程的阶数

初始条件与特解

• 确定通解中常数的条件就是初始条件

一阶微分方程的求解

按类型识别，对号入座

变量可分离型

能写成 $y\prime = f(x)g(y)$形式的方程，解法为

$$\dfrac{dy}{dx}=f(x)g(y) \implies \int \dfrac{dy}{g(y)}=\int f(x)dx$$ $$\text{例如} \dfrac{dy}{dx}=e^{x-y}=e^x\cdot e^{-y} \implies \int e^ydy = \int e^xdx= \begin{cases} e^y=e^x+C\text{隐式解}, \cr y=ln(e^x+C)(显式解) \end{cases}$$

解决除过去丢解的方法：不用解决，大纲只要求通解，不要求求全部解

可化为变量可分离型

(1) 形如$\dfrac{y}{dx}=f(ax+by+c)$的方程，其中常数a,b全都不为零，其解法为令$u=ax+by+c$,则$\dfrac{u}{dx}=a+b\dfrac{dy}{dx}$，代入原方程得$\dfrac{du}{dx}a+bf(u)$，见例1.13.2

(2) 齐次型微分方程

• $\dfrac{y}{x}=\varphi(\dfrac{y}{x})$
• $\dfrac{x}{y}=\varphi(\dfrac{x}{y})$

一阶线性微分方程

$y\prime + p(x)y=q(x)$通解为

$y=e^{-\int p(x)dx}[\int e^{\int p(x)dx}\cdot q(x)dx+C]$

求解出来$\int p(x)dx=ln|\varphi(x)|$,可不加绝对值

一阶线性微分方程的通解的例题

伯努利方程

$y’+p(x)y=q(x)y^n(n \neq 0,1)$的方程，其中$p(x),q(x)$为已知的连续函数，具体解法为

(1) 先变形为$y^{-n} \cdot y\prime + p(x)y^{1-n}=q(x)$

(2)令$z=y^(1-n),\text{得}\dfrac{dz}{dx}=(1-n)y^{-n}\dfrac{dy}{dx},\text{则}\dfrac{1}{1-n} \cdot \dfrac{dz}{dx}+p(x)z=q(x)$

伯努利方程的例题

二阶可降阶微分方程的求解

$y\prime\prime=f(x,y\prime)$型

不显含y

求解方法

例题

$y\prime\prime=f(y,y\prime)$型

不显含x

求解方法

例题

高阶线性微分方程的求解

概念

二阶变系数线性微分方程：不考

只考二阶常系数线性微分方程

图片详情

解的结构(以二阶为例)

图片详情

二阶常系数齐次线性微分方程的通解

$\bigstar$

图片详情

其中： $\alpha=-\dfrac{p}{2},\qquad \beta=\dfrac{\sqrt{4q-p^2}}{2}$

二阶常系数非齐次线性微分方程的特解

$\bigstar$(考研大纲有独特的方法)

$\color{green}{\text{一句话：}}$ 先解齐次，将特解带入

图片详情

例1.13.8

例1.13.9 $\color{red}{\text{}}$

n阶常系数线性微分方程的解

$\mho$(基础阶段不说强化班再提)

图片详情

无穷级数

• 主要是三类问题：判敛，求和，展开
• 可以和前面的不等式和数列极限配合着来看，把对应不等式的题目标记到对应知识点的旁边 $\mho$

常数项级数

常数项级数的概念与性质

引言

概念及其敛散性

给定一个无穷数列，将其各项用加号连起来得到的记号$\displaystyle \sum_{n=1}^{\infty}u_n$叫做无穷级数

${\textstyle\unicode{x2460}}$ 写$S_n$

${\textstyle\unicode{x2461}}$ 求$\displaystyle \lim_{n \to \infty}S_n$

性质

性质1 收敛级数的线性性质:两个级数收敛，求和必然收敛

性质2 改变级数任意有限项，不会改变该级数的敛散性

$\bigstar$ $\bigstar$ $\bigstar$ 性质3 如果级数收敛，通项必然趋于0

级数的敛散性的判别方法

• 4分或10分
• 5+1判别
• 两个概念（绝对收敛，条件收敛）

正项级数及其敛散性判别

一共五种方法

5+1(莱布尼茨)判别法

三个好朋友

• p级数：p206注2
  • 
• $\bigstar$ 广义p级数$\displaystyle \sum_{n=2}^{\infty}\dfrac{1}{n(lnn)^p}$,跟p级数的敛散性一致
• 等比级数 $\displaystyle \sum_{n=1}^\infty aq^{n-1} ,$

  收敛原则

  充分必要条件是它的部分和数列${S_n}$有界

比较判别法

两个正项级数，若大的收敛，则小的必收敛；若小的发散，则大的必发散

$\bigstar$ 比较判别法的极限形式

比阶

例子(讲了无数遍的等价无穷小替换)：

将每一项看成x

比值判别法(也叫达朗贝尔判别法)

• $\bigstar$

后一项比前一项，的比值大于1发散，小于1收敛

用来解决形如 $a^n,n!,n^n$

根值判别法(也叫柯西判别法)

• 比较适合形如$a^n,n^n$,但是$n!$不考虑

  交错级数及其敛散性判别

  若级数正负相间出现，称这样的级数为交错级数

不能出现有0的项

莱布尼茨判别法

单调不增，且通项趋向于0，级数收敛

任意项级数及其敛散性判别

若级数各项可正，可负，可为零，称这样的级数为任意项级数

任意项=正向+交错级数

给任意项级数的每一项加上绝对值，写成$\displaystyle \sum{n=1}|u_n|$,这样，就使得$|u_n| \geq 0$,成了正项级数，它叫作原级数$\displaystyle \sum{n=1}^\infty$的绝对值级数

绝对收敛

条件收敛

本来是收敛的，加了绝对值就不收敛了

收敛级数的性质

性质4 收敛级数的项任意加括号后所得的新级数仍收敛,且其和不变.

性质5﹑若原级数绝对收敛,不论将其各项如何重新排列,所得的新级数也绝对收敛,且其和不变.(这个性质就是在说:绝对收敛的级数具有可交换性,此性质是德国数学家狄利克雷给出的.)

抽象级数的收敛问题 $\spadesuit$(p209:例1.14.11的注)

幂级数

幂级数及其收敛域

概念

图片详情

(1)函数项级数

(2)幂级数

(3)收敛点与发散点

(4) 收敛域

阿贝尔定理

当幂级数$\displaystyle \sum{n=0}^\infty a_nx^n\text{在点}x=x_1(x_1 \neq 0)\text{处收敛时，对于满足}|x|<|x_1|\text{的一切}x,\text{幂级数绝对收敛};\text{当幂级数}\displaystyle \sum{n=0}^\infty a_nx^n \text{在点}x=x_2(x_2 \neq 0)\text{处发散时，对于满足}|x|>|x_2|\text{的一切}x,\text{幂级数发散}$

但在对应的R点需要带进去用到之前的知识解决（端点处一定要单独讨论）

收敛域的求法

${\textstyle\unicode{x2460}}$ 求比值

${\textstyle\unicode{x2461}}$ 单独确定

$\bigstar$ $\spadesuit$(p210:原文) 求收敛域的统一方法【高数18讲（上面的课本方法缺项解决不了）】：$\sum u_n(x)$

${\textstyle\unicode{x2460}}\text{记}|u_n(x)| \geq 0$

${\textstyle\unicode{x2461}}\text{用}\displaystyle \lim{n \to \infty} \dfrac{|u{n+1}|(x)}{|u{n}|(x)}=\rho\text{或}\displaystyle \lim{n \to \infty}\sqrt{|u_n(x)|}=\rho,\text{令} \rho < 1 \implies x \in(a,b)$(收敛区间)

${\textstyle\unicode{x2462}}$单独讨论x=a，x=b的收敛性 $\implies$ 收敛域

$\bigstar$ $\mho$ $\spadesuit$(p210:具体内容) 抽象问题

• 条件收敛的情况是重要考点

幂级数求和函数

• 求和11分

概念

注：通过看书，发现只在收敛域上讨论和函数，所以x取值范围代表收敛域

运算法则

$\spadesuit$(p203:具体内容) 两个级数的下标相同，次数相同才能相加

• 通项、下标一起变
• 只变下标，不变通项
• 只变通项，不变下标

性质

重要展开式

图片详情

函数展开成幂级数

• 展开10分

概念

求法

直接法

间接法

数一专题内容(应用题)

一元函数微分学

• 没什么难点基本上都是套公式
• 投入产出比很高

物理应用

导数的物理意义，速度和加速度

相关变化率

• $\bigstar$ 5分 或 10分，必考无疑

几何应用

一元函数积分学应用

物理应用

相关变化率

• $\bigstar$ $\dfrac{dA}{dB}=\dfrac{dA}{dC}\cdot\dfrac{dC}{dB}$

几何应用

• 曲率公式：$k=\dfrac{|y\prime\prime|}{[1+(y\prime)^2]^{\frac{3}{2}}}$
• 曲率半径(曲率的倒数)：$R=\dfrac{1}{k}=\dfrac{[1+(y\prime)^2]^{\frac{3}{2}}}{|y\prime\prime|}(y\prime\prime\neq0)$

一元函数积分学应用

物理应用

变力沿直线做功

抽水做功

$\bigstar$ 一直在猜会出这种题

水压力(静水压力)

• 2020
• 主要确定平板的宽度，
• $\blacktriangleright$(为什么只跟宽度有关系)

几何应用

“平面上的曲边梯形”的形心坐标公式

$\bar{x} = \dfrac{\int_a^bxf(x)dx}{\int_a^bf(x)dx}$

• $\blacktriangleright$ 推导过程，0到f(x)的积分为什么是f(x) :积分带进去就是了

$\bar{y} = \dfrac{1}{2}\dfrac{\int_a^bf^2(x)dx}{\int_a^bf(x)dx}$

平面曲线弧长

旋转曲面的表面积

平行截面为已知的立体体积

微分方程的物理应用

牛顿第二定律

• 表达式里可以不出现t
  • $a=v\cdot\dfrac{dv}{dx}$

变化率问题

• $\bigstar$ $\dfrac{dA}{dB}$
• $\bigstar$ $\bigstar$ $\bigstar$ 传染病模型

欧拉方程

• 跟常系数微分方程作比较

傅里叶级数

• 送分题
• 展开为三角函数
  • 对比展开为幂函数

${\textstyle\unicode{x2461}}$ 奇偶延拓

• 如果函数是偶函数，展开为余弦级数
• 如果函数是奇函数，展开为正弦级数
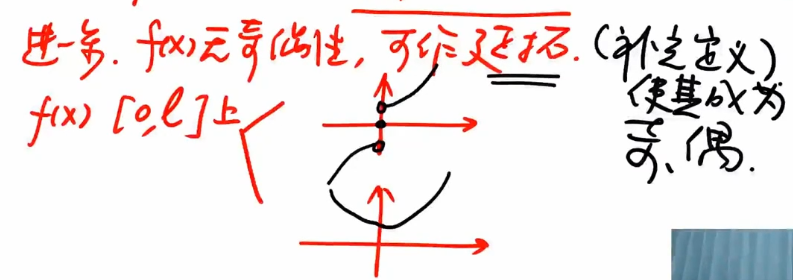
• 无奇偶性，可以作延拓(相当于补充定义)

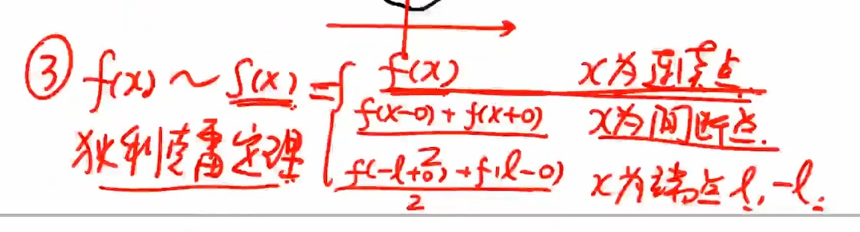
${\textstyle\unicode{x2462}}$ 迪利克雷收敛性定理

• 连续函数才相等，

多元函数积分学的基础知识

服务于第18讲

切一刀，转一周，投下来

向量代数

向量及其表达形式

向量的运算与应用

点积为零，垂直关系

数量积及其应用

向量积及其应用

混合积及其应用

向量的方向角和方向余弦

空间平面与直线

平面方程

一般式

点法式

三点式

截距式

直线方程

一般式

点向式

参数式

两点式

位置关系

距离

直线的关系

平面的关系

直线与平面的关系

空间曲线与曲面

空间曲线

一般式

参数方程

空间曲线在坐标面上的投影

• $\bigstar$ $\bigstar$ $\bigstar$
• 往哪个面投，就消去哪个字母

任意面，任意直线的投影：平面束

空间曲线与曲面

曲面方程

二次曲面

曲面名称	方程	图形
椭球面	$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2}=1$ $\bigstar$ 注意球面:$x^2=y^2=z^2=a^2$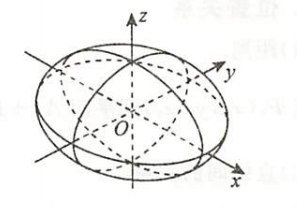
单叶双曲面	$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2}=1$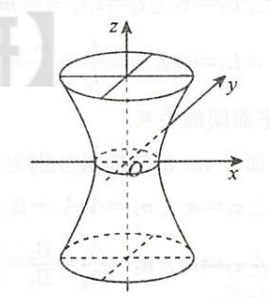
双叶双曲面	$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2}=1$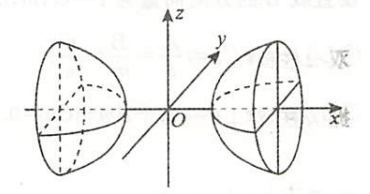
椭圆抛物面	$\dfrac{x^2}{2p}+\dfrac{y^2}{2q}=z(p,q>0)$ $\bigstar$ 注意旋转抛物面:$x^2+y^2=z$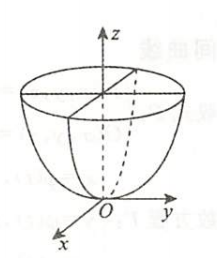
椭圆锥面	$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = \dfrac{z^2}{c^2}$ $\bigstar$ 注意锥面:$z=\sqrt{x^2+y^2}$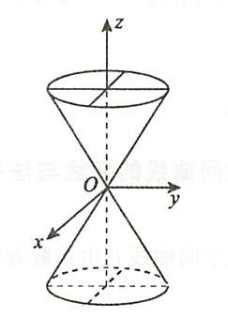
双曲抛物面(马鞍面)1	$-\dfrac{x^2}{2p}+\dfrac{y^2}{2q}=z(p,q>0)$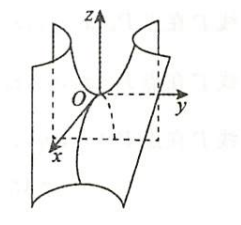
双曲抛物面(马鞍面)2	$\bigstar$非常有趣 $z=xy$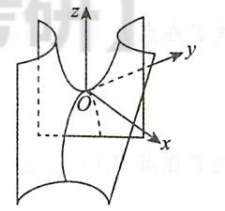

柱面

旋转曲面

• $\bigstar$ $\bigstar$
• 口诀

$$\begin{cases} {\textstyle\unicode{x2460}} \text{绕着谁转谁不变(绕z转，z不变)} , & \cr {\textstyle\unicode{x2461}} \text{另一个字母写成另两个字母的}\sqrt{\text{平方和}}, & \end{cases}$$

多元函数微分学的几何应用

空间曲线的切线与法平面

• 4分

参数方程给出

交面式方程给出

空间曲面的切平面与法线

• $\bigstar$ $\bigstar$ $\bigstar$

隐式给出

显式给出

场论初步

方向导数

• 在之前学的知识里面，偏导数也只是x轴，y轴，z轴方向上的变化率，并不涉及到任意方向上的变化率

梯度

方向导数与梯度的关系

散度

• $\sharp$ 解释再多最后也只是考一个公式
• 在一个点的发散程度
• 一道题就能解决问题，无非就是凑公式往里面套

选度

• 一道题就能解决问题，无非就是凑公式往里面套

三重积分与曲线曲面积分

• 集高等数学与一身

三重积分

三重积分的概念、性质与对称性

概念

• 可以用密度与质量去理解

性质

性质1(求空间区域的体积)

性质2(可积函数必有界)

性质3(积分的线性性质)

性质4(积分的可加性)

性质5(积分的保号性)

性质6(三重积分的估值定理)

性质7(三重积分的中值定理)

$\bigstar$ 对称性

普通对称性

图片详情

轮换对称性

图片详情

三重积分的计算

基础方法

直角坐标系

先一后二

别称(先$z$后$xy$法，也叫投影穿线法)

适用场合：$\Omega$有下曲面$z=z_1(x,y)$、上曲面$z=z_2(x,y)$.无侧面或侧面为柱面

计算方法：

$$\iiint_\Omega f(x,y,z)dv=\iint_{D_{xy}}d\sigma \int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dz$$

步骤口诀

• 后积先定限
• 限内画条线
• 先交写下限
• 后交写上限

先二后一

别称(先$xy$后$z$法，也叫定限截面法)

适用场合：$\Omega$是旋转体，其旋转曲面方程为$\Sigma:z=z(x,y)$

计算方法：

$$\iiint_\Omega f(x,y,z)dv=\int_a^bdz \iint_{D_z}f(x,y,z)d\sigma$$

步骤口诀

• 后积先定限
• 限内截个面

柱面坐标系

• 定积分+极坐标系下的二重积分(先二后一法)

在直角坐标系的先一后二法中，若$\iint{D{xy}}适用于极坐标系，$

$$\text{则}\begin{cases} x = rcos\theta , & \cr y = rsin\theta , & \cr \end{cases} \text{便有}$$ $$\iiint_\Omega f(x,y,z)dxdydz = \iiint_\Omega f(rcos \theta,r sin\theta,z)rdrd\theta dz$$

球面坐标系

适用场合

• 被积函数中含$f(x^2+y^2+z^2)\text{、}f(x^2,y^2)$

计算方法

$$\text{令}\begin{cases} x=rsin(\varphi)cos\theta, & \cr y=rsin(\varphi)sin\theta, & \cr z=rcos(\varphi), & \end{cases}$$

计算公式

$$\iiint_\Omega f(x,y,z)dxdydz = \iiint_\Omega f(rsin(\varphi)cos\theta,rsin(\varphi)sin\theta,rcos(\varphi))r^2sin(\varphi)d\theta d \varphi dr$$

技术方法

对称性

形心公式的逆用

第一型曲线积分

概念、性质与对称性

概念

• 定积分定义在“直线段”上，第一型曲线积分定义在“曲线段”上

性质

性质 8 (求空间曲线的长度)

性质9 (可积函数必有界)

性质10 (积分的线性性质)

性质11 (积分的可加性)

性质12(积分的保号性)

性质13(第一型曲线积分的估值定理)

性质14(第一型曲线积分的中值定理)

对称性

普通对称性

图片详情

轮换对称性

图片详情

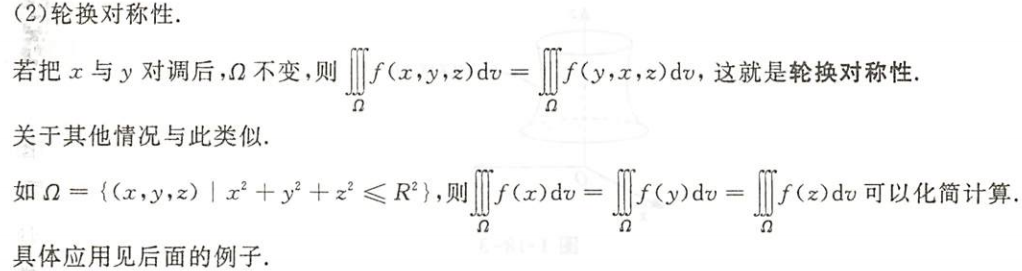
计算

基础方法-化为定积分

空间形式

${\textstyle\unicode{x2460}}$ 参数式

空间形式的计算公式

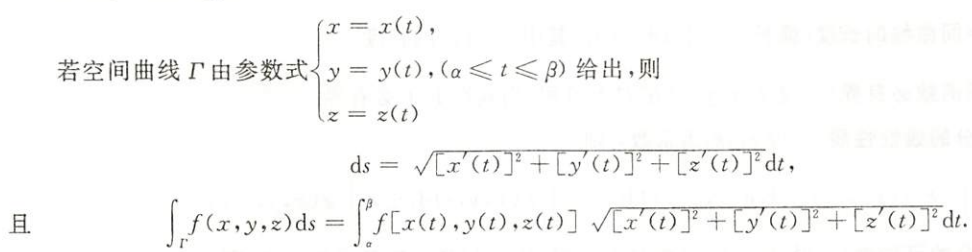
平面情形

${\textstyle\unicode{x2460}}$ 显式

${\textstyle\unicode{x2460}}$ 参数式

${\textstyle\unicode{x2460}}$ 极坐标形式

平面情形的计算方法

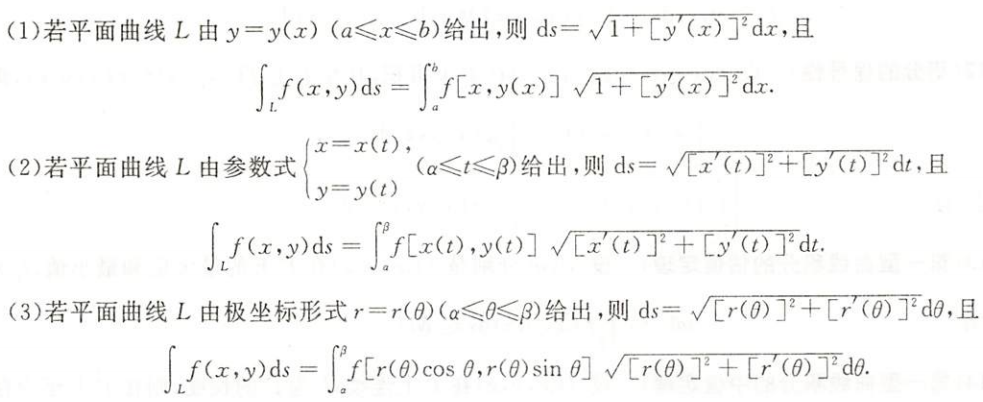
技术方法

边界方程代入被积函数

对称性

形心公式的逆用

图片详情

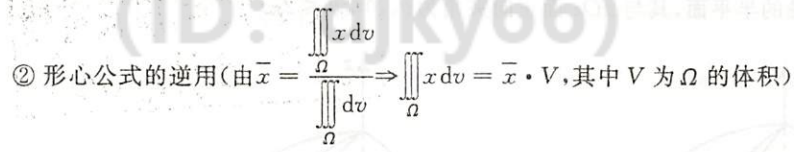
第一型曲面积分

跟二重积分对比

概念性质与对称性

概念

性质

对称性

普通对称性

轮换对称性

计算

基础方法-化为二重积分

基础方法-化为二重积分

技术方法

边界方程代入被积函数

对称性

形心公式的逆用

应用

重积分与第一型线面积分的应用

一个体系:二重、三重、一线、一面

几何量

平面区域

图片详情

面积

空间区域

体积

图片详情

空间曲线

弧长

图片详情

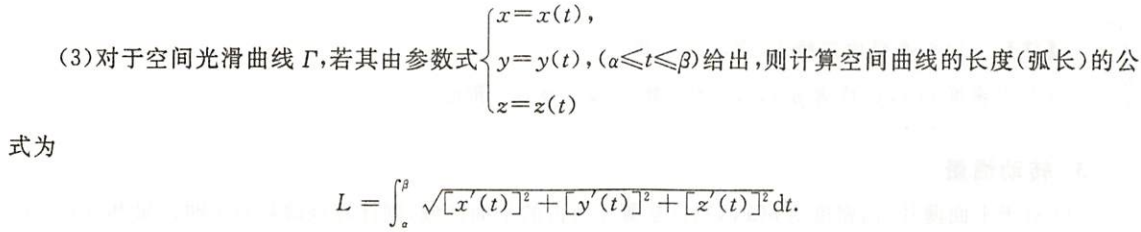
空间曲面

面积

图片详情

重心(质心)与形心

• 密度是常数的时候，重心就是形心

形心公式的逆用

平面薄片

图片详情

空间物体

• $\bigstar$ 喜欢用三重积分考重心

图片详情

空间曲线

图片详情

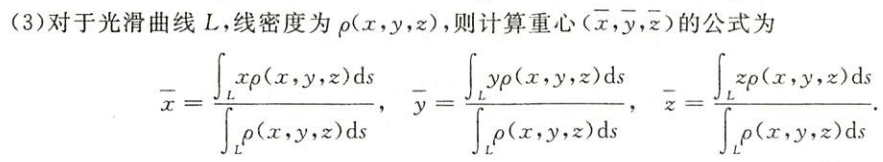
空间曲面

图片详情

转动惯量

• 从未考过，未来会考

平面薄片

图片详情

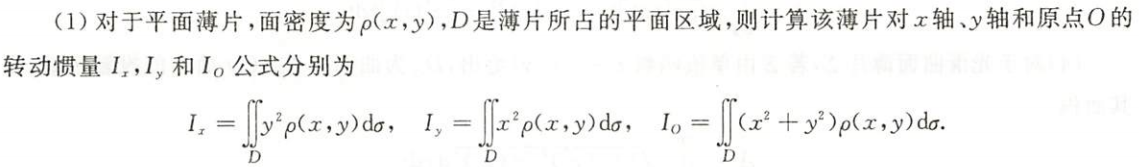
空间物体

图片详情

空间曲线

图片详情

空间曲面

图片详情

引力

平面薄片

图片详情

空间物体

图片详情

空间曲线

图片详情

空间曲面

图片详情

第二型曲线积分

• 既有长度也有方向
• 变力沿着曲线做功

对称性问题

第二型曲线积分的概念与性质

场的概念

图片详情

变力沿曲线做功

图片详情

第二型曲线积分的概念

图片详情

第二型曲线积分的性质

图片详情

平面第二型曲线积分的计算

基础方法-化为定积分

图片详情

格林公式法

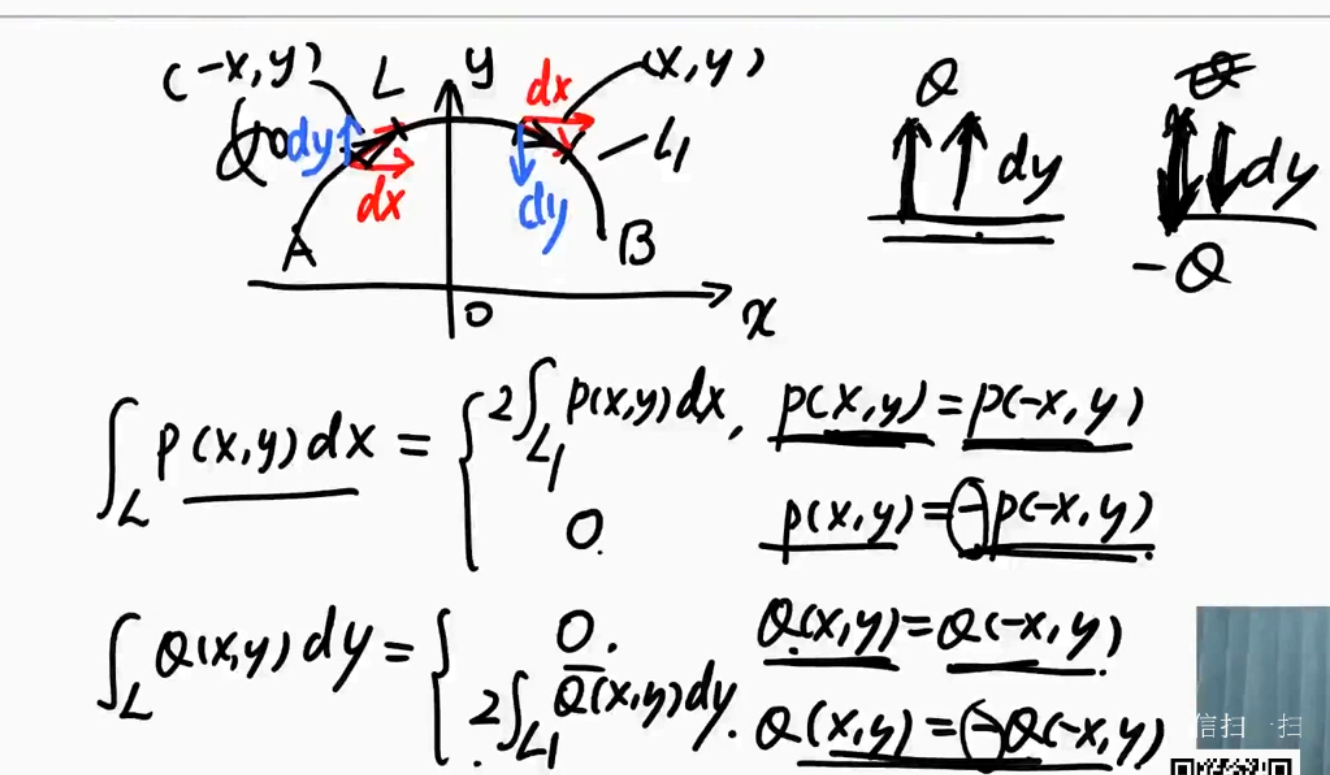
• $\bigstar$ $\bigstar$ $\bigstar$
• 公式的使用一定保证D是封闭区域（L是封闭曲线）
• 左手在D内，为L的正向，记为$L^+$(反向要添负号)
• $P\text{、}Q$有一阶连续偏导数
• 形心公式的逆用

第二型曲面积分

• 研究通量的概念
• 流出为正，流入为负
• 跟投影的轴锐角为正，钝角为负
• 海域找源头

外法向（题目告知）

第二型曲面积分的概念与性质

向量场的通量

图片详情

第二型曲面积分的概念

图片详情

$$\iint_{\Sigma}P(x,y,z)dydz + Q(x,y,z)dzdx + R(x,y,z)dxdy$$

第二型曲面积分的性质

图片详情

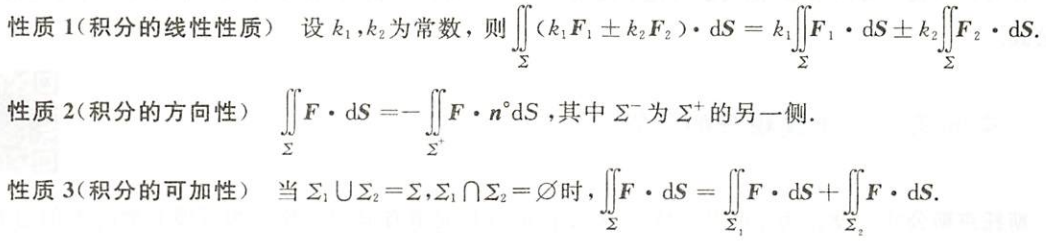
性质1(积分的线性性质)

性质2(积分的方向性)

性质3(积分的可加性)

第二型曲面积分的计算

基本方法-化为二重积分

拆成三个积分，分别投影到相应的坐标面上，化为二重积分计算，然后再相加,以$R(x,y,z)dxdy$为例子

(1) 将$\Sigma$投影到某一平面(比如$xOy$面)上$\implies$投影区域为$D$(比如$D_{xy}$)

(2) 将$z=z(x,y)$或者$F(x,y,z)=0$代入$R(x,y,z)$

(3) 将$dxdy$写成“$\pm dxdy$”,其中$\Sigma$方向向上(即法向量与z轴夹角为锐角)时取“+”,否则取“—”.

这就把第二型曲面积分化为了二重积分,得到

$$\iint_{\Sigma}R(x,y,z)dxdy=\pm \iint_{D_{xy}}R(x,y,z(x,y))dxdy$$

同样需要指出的是，投影时$\Sigma$上的任何两点的投影点不能重合

图片详情

高斯公式法

• ${\textstyle\unicode{x2460}} \Sigma$封闭曲面(封闭的区域$\Omega$)
• ${\textstyle\unicode{x2461}} \Omega$取外侧
• ${\textstyle\unicode{x2462}} P,Q,R$具有一阶连续偏导数

$$\unicode{x222F}_\Sigma Pdydz + Qdzdx + Rdxdy = \iiint_\Omega (\dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z})dv$$

需要掌握“补面法”和“挖去法”

例题1

例题2

空间第二型曲线积分的计算

斯托克斯公式

• 选平面最简单

$$\unicode{x222E}_l Pdx+Qdy+Rdz = \iint_\Sigma \begin{vmatrix} cos\alpha & cos \beta & cos \gamma \cr \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial }{\partial z} \cr P & Q & R \end{vmatrix} dS$$

基本求导公式

公式	题目
$(x^a)\prime=ax^{a-1}\text{(a为常数)}$
$(a^x)\prime=a^xlna(a>0,a\neq 1)$
$(e^x)\prime=e^x$
$(log_ax)\prime=\dfrac{1}{xlna}(a>0,a\neq 1)$
$(ln x)\prime=\dfrac{1}{x}$
$(sin x)\prime=cos x$
$(cos x)\prime=-sin x$
$(arcsin x)\prime=\dfrac{1}{\sqrt{1-x^2}}$
$(arccos x)\prime=-\dfrac{1}{\sqrt{1-x^2}}$
$(tan x)\prime=sec^2x$	1
$(cot x)\prime=-csc^2x$
$(arctan x)\prime=\dfrac{1}{1+x^2}$
$(arccot x)\prime=-\dfrac{1}{1+x^2}$
$(sec x)\prime=sec x tan x$
$(csc x)\prime=-csc x cot x$
$[ln(x + \sqrt{x^2+1})]’=\dfrac{1}{\sqrt{x^2+1}}$
$[ln(x + \sqrt{x^2-1})]’=\dfrac{1}{\sqrt{x^2-1}}$

跟 $\color{red}{\text{cos}}$ 相似度高的都会出现 $\color{green}{\text{负号}}$

基本积分表

公式	题目
$\int x^kdx=\dfrac{1}{k+1}x^{k+1}+C,k\neq-1$
$\int \dfrac{1}{x^2}dx=-\dfrac{1}{x}+C$
$\int \dfrac{1}{\sqrt{x}}dx=2\sqrt{x}+C$
$\int \dfrac{1}{x}dx=ln\lvert x\rvert+C$
$\int e^xdx=e^x+C$
$\int a^xdx=\dfrac{a^x}{ln a}+C,(a >0 \text{且} a \neq 1)$
$\int e^xdx=e^x+C$
$\int sinxdx=-cosx+C$
$\int cos xdx=sin x+C$
$\int tan xdx=-ln\lvert cos x \rvert+C$
$\int cot xdx=ln\lvert sin x \rvert+C$
$\int\dfrac{dx}{cosx}=\int secxdx=ln\lvert secx+tanx \rvert+C$	1
$\int\dfrac{dx}{sinx}=\int cscxdx=ln\lvert cscx-cotx \rvert+C$
$\int sec^2xdx=tanx+C$
$\int csc^2xdx=-cotx+C$
$\int secxtanxdx=secx+C$
$\int cscxcotxdx=-cscx+C$
$\int \dfrac{1}{1+x^2}dx=arctanx+C$
$\int \dfrac{1}{a^2+x^2}dx=\dfrac{1}{a}arctan\dfrac{x}{a}+C$
$\int\dfrac{1}{\sqrt{1-x^2}}dx=arcsinx+C$
$\int\dfrac{1}{\sqrt{a^2-x^2}}dx=arcsin\dfrac{x}{a}+C$
$\int\dfrac{1}{\sqrt{x^2+a^2}}dx=ln(x+\sqrt{x^2+a^2})+C(\text{常见}a=1)$
$\int\dfrac{1}{\sqrt{x^2-a^2}}dx=ln\lvert x+\sqrt{x^2-a^2} \rvert+C(\lvert x\rvert>\lvert a \rvert)$
$\int\dfrac{1}{x^2-a^2}dx=\dfrac{1}{2a}ln\lvert \dfrac{x-a}{x+a} \rvert+C(\int \dfrac{1}{a^2-x^2}dx=\dfrac{1}{2a}ln \lvert \dfrac{x+a}{x-a} \rvert +C)$
$\int\sqrt{a^2-x^2}dx=\dfrac{a^2}{2}arcsin\dfrac{x}{a}+\dfrac{x}{2}\sqrt{a^2-x^2}+C$
$\int sin^2xdx=\dfrac{x}{2}-\dfrac{sin 2x}{4}+C(sin^2x=\dfrac{1-cos2x}{2})$
$\int cos^2xdx=\dfrac{x}{2}+\dfrac{sin 2x}{4}+C(cos^2x=\dfrac{1+cos2x}{2})$
$\int tan^2xdx=tanx-x+C(tan^2x=sec^2x-1)$
$\int cot^2xdx=-cotx-x+C(cot^2x=csc^2x-1)$

华里士公式（点火公式）

• 
• 

常用不等式

可以从图像和意义去理解，比如绝对值相当于距离,几何平均值和算数平均值可以画图

$$\text{(1) 设a,b为实数，则} {\textstyle\unicode{x2460}} |a \pm b| \leq |a|+|b|; \quad {\textstyle\unicode{x2461}} ||a|-|b|| \leq |a-b|$$

将 ${\textstyle\unicode{x2460}}$ 式子推广为:

离散情况:设$a_1,a_2,\cdots,a_n$为实数，则

$$|a_1\pm a_2 \pm \cdots \pm a_n| \leq |a_1| + |a_2| + \cdots + |a_n|$$

连续情况：设$f(x)$在$ [ a,b ] (a < b)$上可积，则

$$|\int_a^bf(x)dx| \leq \int_a^b|f(x)|dx$$ $$(2) {\textstyle\unicode{x2460}} \dfrac{2}{\frac{1}{a}+\frac{1}{b}} \leq \sqrt{ab} \leq \dfrac{a+b}{2} \leq \sqrt{\dfrac{a^2+b^2}{2}}(a,b>0);\quad \text{(调和平均数≤几何平均数≤算术平均数≤平方平均数)}$$ $${\textstyle\unicode{x2461}} \dfrac{2}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} \leq \sqrt[3]{abc}\leq \sqrt{\dfrac{a^2+b^2+c^2}{3}}(a,b,c>0);$$ $$\text{(3) 设a > b > 0,则} \begin{cases} \text{当}n>0时,a^n > b^n, & \cr \text{当}n<0时,a^n < b^n, & \end{cases}$$ $$\text{(4)若}0<a<x<b,0<c<y<d.\text{则} \dfrac{c}{b} < \dfrac{y}{x} < \dfrac{d}{a}$$ $$\text{(5)} sinx<x<tanx(0 <x<\dfrac{\pi}{2})$$ $$(6) sinx<x(x>0)$$ $$(7) arctanx \leq x \leq arcsinx(0 \leq x \leq 1)$$ $$(8)e^x \geq x+1(\forall x)$$ $$(9) x-1 \geq ln x(x>0)$$ $$(10) \dfrac{1}{x+1} <ln(1+\dfrac{1}{x})<\dfrac{1}{x}(x>0)$$

图片详情

因式分解公式

$(a+b)^2=a^2+2ab+b^2, \qquad (a-b)^2=a^2-2ab+b^2,$

$(a+b)^2=a^3+3a^2b+3ab^2+b^3, \qquad (a-b)^2=a^2-2ab+b^2,$

$(a+b)^3=a^3+3a^2b+3ab^2+b^3, \qquad (a-b)^3=a^3-3a^2b-3ab^2+b^3,$

$a^2-b^2=(a+b)(a-b), \qquad a^3-b^3=(a-b)(a^2+ab+b^2),$

$a^3+b^3=(a+b)(a^2-ab+b^2)$

$a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+\cdots+ab^{n-2}+b^{n-1})(n是正整数)$

$n\text{是正偶数时},a^n-b^n=(a+b)(a^{n-1}-a^{n-2}b + \cdots + ab^{n-2}-b^{n-1})$

$n\text{是正奇数时},a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b + \cdots - ab^{n-2}+b^{n-1})$

$\text{二项式定理}(a+b)^n=\displaystyle \sum_{k=0}^n C_n^ka^{n-k}b^k$

p27

n次的二项展开有n+1项，杨辉三角推系数

常用的等价无穷小

当$x\to 0$时，常用的等价无穷小有

$sin x \backsim x,\qquad tanx \backsim x,\qquad arcsinx \backsim x,\qquad 1-cosx \backsim \dfrac{1}{2}x^2,$

$arctan x \backsim x,\qquad ln(1+x) \backsim x,\qquad e^x-1 \backsim x,$

$a^x -1 \backsim xlna, \qquad (1+x)^a-1 \backsim ax,$

特别的，当$x\to x_0$时，若$f(x) \to 0,g(x) \to 0,\text{则}e^{f(x)}-e^{g(x)} \backsim f(x)-g(x)$

重要函数的泰勒展开

p43

注意$x\to0$

$sin x = x - \dfrac{x^3}{3!}+o(x^3), \qquad \qquad arcsin x = x + \dfrac{x^3}{3!}+o(x^3),$

$tanx =x + \dfrac{x^3}{3}+o(x^3),\qquad \qquad arctan x = x - \dfrac{x^3}{3}+o(x^3),$

$ln(1+x) =x-\dfrac{x^2}{2}+\dfrac{x^3}{3}+o(x^3),$

$e^x = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + o(x^3), \qquad (1+x)^\alpha =1+\alpha x +\dfrac{\alpha(\alpha-1)}{2!}x^2+o(x^2)$

$cosx =1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}+o(x^4),$

---

初等函数的幂级数展开式

图片详情

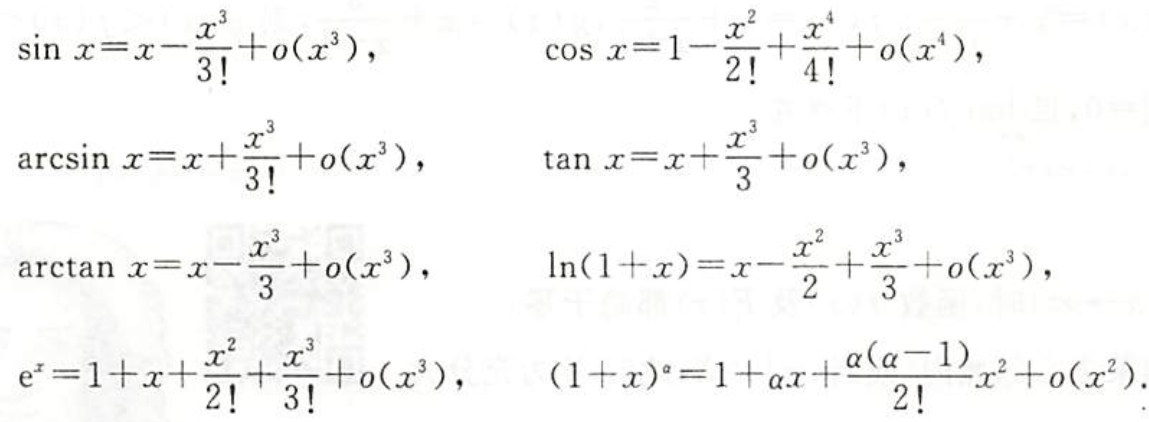
记忆方法(每一行都是一对)：

• 去了 正切 分母都是幂阶乘,
• 正弦正切你负我正真相称,
• 余弦对数2把兄弟做(除了这两货，其他都没有2的系数)

规律：

• sin，arcsin，tan，arctan，ln都是从1次开始
  • sin tan 系都是1，3
  • ln系是1，2，3
• 自然指数，幂函数，余弦函数都是0次开始
  • 自然指数是0，1，2，3
  • 幂函数是0，1，2
• 余弦函数是
  • 0，2，4

倒背如流，背系数(方法：在做题中背)