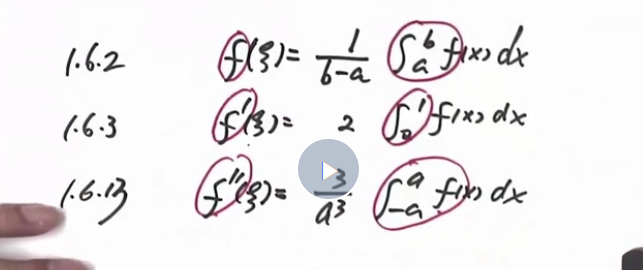zy2022
高等数学
高等数学-ch6.十大定理及其使用
pp.92
十大定理及其使用
- 定理1-4为函数定理
- 定理5-9为导数定理
- 定理10为积分定理
- 对比着看
- $\dagger$(1.6.1) 离散的平均值定理:平均值定理
- $\dagger$(1.6.2) 连续的平均值定理:积分中值定理
$\sharp$ 讲课风格:概念-练习-总结(升华)
定理1:有界与最值定理
$m \leq f(x) \leq M$,其中$m$,$M$分别为$f(x)$在$[a,b]$上的最小值与最大值
$\color{green}{\text{意义:}}$ 函数一定在最大值和最小值之间
定理2:介值定理
当$m \leq \mu \leq M$时,存在$\xi \in [a,b]$,使得$f(\xi)=\mu$
$\color{green}{\text{意义:}}$ 如果一个数在最大值和最小值之间,位于 $\xi$ 处的点可以取到这个值
- 信号:看到区间给的是闭区间
定理3:平均值定理
当$a<x_1<x_2<\cdots<x_n<b$时,在$[x_1,x_n]$内至少存在一点$\xi$,使$f(\xi)=\dfrac{f(x_1)+f(x_2)+\cdots+f(x_n)}{n}$
$\color{green}{\text{意义:}}$ 位于 $\xi$ 处的点为所有数的平均值
- 证明
- 连续型和离散型两种考法
- 看到函数值加加加,就想到除以其个数
- p93 习题1.6.2
$\bigstar$(真题,12年) $\dagger$(1.6.7)
定理4:零点定理
当$f(a)\cdot f(b)<0$时,存在$\xi \in(a,b)$,使得$f(\xi)=0$
$\color{green}{\text{意义:}}$ 函数出现正负变化,位于 $\xi$ 处的点,能取到0
- 由介值定理推出来
$\bigstar$(可能会考证明题) 定理5:费马定理
$$
\text{设}f(x)\text{满足在}x_0\text{处}\begin{cases}
{\textstyle\unicode{x2460}} \text{可导}, \cr
{\textstyle\unicode{x2461}} \text{取极值},
\end{cases}
\text{则}f’(x)=0
$$
- $\bigstar$(${\textstyle\unicode{x2460}}$) 可导+极值(区间内部的最值) $\implies$ $f’(x_0)=0$
- 一定要快,不要拖泥带水
- $\bigstar$(${\textstyle\unicode{x2461}}$)证明
- 脱帽法值严格的不等
- 戴帽法是非严格的不等
- $\bigstar$(${\textstyle\unicode{x2462}}$) $\dagger$(1.6.8)达布定理(也叫导数介值定理)
- ch5讲过
- 端点处无法用费马定理
- 费马定理的应用:当一个人跑到最远处时,他的速度为零;当一个人跑的最快的时候他的加速度为0
$\sharp$ 费马大定理 $x^n+y^n=z^n$大于2没有正整数解,经过300+年威尔斯证出来,为了证明这个创立了7门独立的学科
$\sharp$ 值得一看的书:《费马大定理》
$\bigstar$ 导数零点定理
$\bigstar$(特性)) 只要找到导数异号的两个点,中间一定有导数为0的点
- $\spadesuit$(p58:书页标签) 前面讲过的知识 $f’(x) \neq0 \implies f’(x)$保号
- 单调函数必有反函数
$\spadesuit$(p90:1.6.8)
设$f(x)$在$[a,b]$上可导,证明当$f’+(a)\cdot f’-(b)<0$时,存在$\xi\in(a,b)$,使得
$$
f’(\xi)=0
$$
$\clubsuit$ 导数的定义
$\mho$(极限保号,脱帽戴帽法) $\blacktriangleright$(脱帽戴帽法的前提函数连续?)
定理6:罗尔定理
$$
\text{设}f(x)\text{满足} \begin{cases}
{\textstyle\unicode{x2460}} \text{在}[a,b]上连续, \cr
{\textstyle\unicode{x2461}} \text{在}(a,b)\text{内可导,则存在} \xi \in (a,b),\text{使得}f’(\xi)=0\cr
{\textstyle\unicode{x2462}} f(a)=f(b),
\end{cases}
$$
- $f(x)=0$有两个根$\implies$ $f’(x)$至少有一个根
- 抓住两个问题:${\textstyle\unicode{x2460}}$找端点值相同,${\textstyle\unicode{x2461}}$找谁($F(x)$)的端点值相同
- $\spadesuit$(p89:如何构造辅助函数)
- 逆用乘积求导公式
- $\dagger$(1.6.4) $f(x)f’(x) \implies F(x)=f^2(x)$
- $[f’(x)]^2 \implies F(x)=f(x)f’’(x)$
- $[f’(x) + f(x)\varphi’(x)]e^{\varphi(x)} \implies F(x)=f(x)e^{\varphi(x)}$
- 逆用乘积求导公式
- $\spadesuit$(p89:如何构造辅助函数)
费马定理关键是找极值,罗尔定理找端点值相同,都能推出$f’(\xi)=0$
罗尔vs拉格朗日:罗尔证明导数为0,拉格朗日得到导数为一个数,拉格朗日可以推罗尔:斜线变直
zy觉得很显然?没怎么看懂
$\dagger$(1.6.5) $f’(\xi)+df(\xi)=0$
$\dagger$(1.6.6) $f’(\xi)-\lambda[f(\xi)-\xi]=1$
- $\bigstar$(标准题)第二问遇到了困难,第一问是锦囊
$\dagger$(1.6.7) 两次罗尔定理
- $\bigstar$(把罗尔定理用到了极致)
- 可以直接用积分中值定理证明(必须用注里面的方法,因为原定理是闭区间)
证明题见到积分的思路
$$
\text{证明题,见到} \int_a^bf(x)dx= \begin{cases}
{\textstyle\unicode{x2460}} \text{积分中值定理} f(\xi)(b-a) & \cr
{\textstyle\unicode{x2461}} \text{令} F(x)=\int_a^xf(t)dt&
\end{cases}
$$
$\sharp$ $\blacktriangleright$(什么是解题技巧,什么是基本东西) 不能光讲解题技巧忽略了基本的东西,(考题第一题,证明费马定理完了)
$\dagger$(习题1.6.3)$f’(\xi)=(1-\dfrac{1}{3})f(\xi)$
定理7:拉格朗日中值定理
$$
\text{设}f(x)\text{满足} \begin{cases}
{\textstyle\unicode{x2460}} \text{在}[a,b]上连续, \cr
{\textstyle\unicode{x2461}} \text{在}(a,b)\text{内可导}
\end{cases}
\text{使得}
$$
$$f(b)-f(a)=f’(\xi)(b-a)$$
$$\text{或者写成}$$
$$f’(\xi)=\dfrac{f(b)-f(a)}{b-a}$$
- 几何意义:割线与切线平行
- 作用上:$f(b)-f(a)=f’(\xi)(b-a)$
- 常用的:$f(x)-f(x_0)=f’(\xi)(x-x_0)$
- 见到$f-f$想到拉格朗日
- $e^x-1=e^x-e^0=e^\xi\cdot x$
- 联系f与$f’$, 立刻想到拉格朗日
$\dagger$(1.6.9)
$\dagger$(1.6.11)
- 用一次拉格朗日是小题
- 此题用两次是大题
- 不同的两个数要用$\tau$将区间切分
$\flat$(思路预测)
$$
\begin{cases}
{\textstyle\unicode{x2460}} \text{方向:}\text{ 思路(考研)(smart 巧)}
\begin{cases}
\cancel{\text{易}}\text{只在一个点上刷题没有意义} \cr
\cancel{\text{难}}\text{中规中矩}
\end{cases}
\cr
{\textstyle\unicode{x2461}} \text{做题:} \text{做题的数量(但也不用太多,思路正确的题目)} \uparrow
\end{cases}
$$
定理8:柯西中值定理
$$
\text{设}f(x),g(x)\text{满足} \begin{cases}
{\textstyle\unicode{x2460}} \text{在}[a,b]上连续, \cr
{\textstyle\unicode{x2461}} \text{在}(a,b)\text{内可导,则存在}\xi \in(a,b),\text{使得} \cr
{\textstyle\unicode{x2462}} g’(x) \neq 0
\end{cases}
$$
$$
\dfrac{f(b)-f(a)}{g(b)-g(a)} = \dfrac{f’(\xi)}{g’(\xi)}
$$
- ${\textstyle\unicode{x2460}}$ 两次拉格朗日相除证柯西是错误的
- 不知道两个$\xi$是否相等
- ${\textstyle\unicode{x2461}}$ 取$g(x)=x$拉格朗日是柯西的特例
- 柯$\implies$拉$\implies$罗尔
- ${\textstyle\unicode{x2462}}$ ${\textstyle\unicode{x2462}}$ 怎么考
- 一个抽象($f(x)$),一个具体($g(x)$)
- $\dagger$(1.6.12)
一个数不为零往往是在分母上
证明$g’(x) \neq 0$一般用反证法
$\bigstar$(热点,极为重要) 定理9:泰勒公式
$\bigstar$(真题) $\dagger$(1.6.13)
- $\xi$是端点的函数不能往外面提
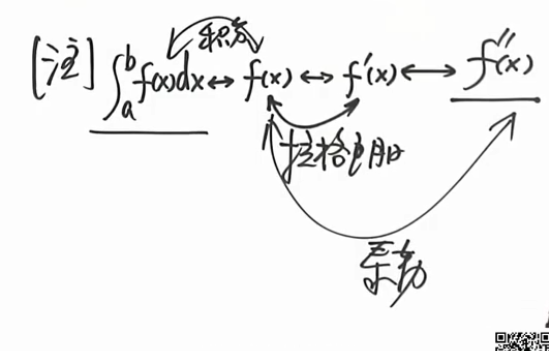
- $f(x)\leftrightarrowd f(x) \leftrightarrow f’(x) \leftrightarrow f’’(x)$
- 总结上面习题得到的知识结构:$\dagger$(1.6.3)
- 习题1.6.5 导数介值定理也是用费马定理证
- 在区间内可导就可以取这个区间内的所有值(要么连续,要么震荡间断点)
带拉格朗日余项的n阶泰勒公式
设$f(x)$在点$x_0$的某个领域内$n+1$阶导数存在,则对该领域内的任意点$x$,有
$f(x)=f(x_0)+f’(x_0)(x-x_0)+\cdots+\dfrac{1}{n!}f^{(n)}(x_0)(x-x_0)^n+\dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}$
其中$\xi$介于$x,x_0$之间
- 最高导数是几就念几阶
- $x_0=0$是麦克劳林展开
- $\spadesuit$(p87:注2几个重要函数的麦克劳林展开)
- $\spadesuit$(p73:4) 用二阶配亚诺余项的麦克劳林展开证明
- 在一个区间处的
带配亚诺余项的n阶泰勒公式
设$f(x)$在点$x_0$处n阶可导,则存在$x_0$的一个领域,对于该领域内的任意点,有
$f(x)=f(x_0)+f’(x_0)(x-x_0)+\dfrac{1}{2!}f’’(x_0)(x-x_0)^2+\cdots+\dfrac{1}{n!}f^{(n)}(x_0)(x-x_0)^n+o((x-x_0)^n)$
- 在一个点处的,局部的,极限的计算题
定理10:积分中值定理
设$f(x)$在$[a,b]$上连续,存在$\xi \in [a,b]$,使得
$$
\int_a^bf(x)dx=f(\xi)(b-a)
$$
- $\spadesuit$(p143:注3)