好好学习
- 视频地址
- 术语规范:书本指的是zy2022,课本指的是同济教材
部分结合同济高等数学教材
回答:什么是基础?
定义、定理、性质要清晰
zy2022:2022考研导学
- 考研数学具有稳定性
- 本质和学科素养
历史沿革
莱布尼茨
$\downarrow$
伯努利
$\downarrow$
欧拉
$\downarrow$
拉格朗日
$\downarrow$
柯西
一道例题
- $\dfrac{0}{0}$形:洛必达法则
- $\bigstar$(必出)泰勒公式: 任何可导$f(x) = \sum a_nx^n$,统一成幂函数,统一美
- $\bigtriangledown$ $o(x^3)+o(x^3)=o(x^3)$,这只是一种记号
- $\bigstar$ $\bigstar$ $x-sinx \sim \dfrac{1}{6}x^3(x \to 0)$
- 打开试卷先找’狗’
- $sinx \to x^1$
- $1- cosx \to \dfrac{1}{2}x^2$
复习建议
基础30讲
习题《1000》型A组
《基础习题》200题
36讲
- 高数18讲
- 现代9讲
- 概率9讲
1000bc
zy2022
习题标记含义:
1.4.1:1(高等数学).4(第四讲).1 (第一题)
高等数学 ch.1
函数的概念与特性
- 此函数非多值函数
函数$y=f(x)$
反函数$y=f^{-1}(x)$
- 严格单调函数必有反函数
- $x=f^{-1}(y)$与$y=f(x)$的图像完全一致。只有把反函数写成$y=f^{-1}(x)$才关于x对称。
- 可以理解为 $f$ 是一种映射方法,$y=f(x)$ 将x轴的值正向映射到y轴的值, $y=f^{-1}(x)$ 将x轴的值反向映射到y轴的值
复合函数$y=f[g(x)]$
- 掌握复合函数的方法
- 解析
- 变量广义化
- 一致单调性
- 值域的解法
- 画图
- 配方
- 求导
$\bigstar$ 四种特性
有界性
- 有界无界必须先指明区间
- 如何证明:找到一个正数$M$使得$|f(x)|\leq M$
单调性
$\mho$(第二点对应的习题)
- 如何证明: $\bigstar$ 求导证明
- 定义法
$\bigstar$ $\clubsuit$ 奇偶性
$\text{设}f(x)\text{是定义在}[-l,l]\text{上的任意函数,则}$
$F_1(x) = f(x) -f(-x) \text{必为奇函数},F_2(x)=f(x)+f(-x) \text{必为偶函数}$
$\text{显然}u(x)=\dfrac{1}{2}[f(x)+f(-x)]\text{是偶函数,} \dfrac{1}{2}[f(x) -f(-x)]\text{是奇函数,}\text{而}$
$f(x) = \dfrac{1}{2}[f(x)+f(-x)] + \dfrac{1}{2}[f(x) -f(-x)]=u(x)+v(x)$
奇函数在0点有定义,$f(0)=0$
偶函数在0点有定义,$f’(0)=0$
$\text{函数}y=f(x)\text{与}y=-f(x)\text{的图形关于x轴对称;函数}y=f(x)\text{与}y=f(-x)\text{的图形关于y轴对称;函数}y=f(x)\text{与}y=-f(-x)\text{的图形关于原点对称}$
函数$y=f(x)$的图形关于直线$x=T$对称的充分必要条件是
$$
f(x)=f(2T-x)\text{或}f(x+T)=f(T-x)
$$
周期性
$\bigstar$ $\bigstar$ $\bigstar$ $\spadesuit$(p6:必考) 7个重要结论
求导之后奇偶性互换
$\sharp$ 拉格朗日中值有什么用:
用导数的大小控制函数的大小
$\bigstar$ $\bigstar$ $\bigstar$ 函数的图像
$\bigtriangledown$ 用微分法和积分法研究函数的性态和测度
直角坐标系下的图像($f(x,y)=0$)
常见图像
基本初等函数与初等函数
基本初等函数:常数函数+反对幂指三
${\textstyle\unicode{x2460}}$见到$\sqrt{u},\sqrt[3]{u}$,用$u$研究最值
$\bigstar$ ${\textstyle\unicode{x2461}}$见到$|u|$用$u^2$研究最值
${\textstyle\unicode{x2462}}$ 见到$\dfrac{1}{u}$,用$u$即可研究最值,$u>0$
$$\bigstar {\textstyle\unicode{x2463}}\text{见到} u_1 u_2 \cdots u_n = u \text{用} ln u = \displaystyle\sum_{i=1}^n ln u_i$$
指数函数
对数函数
$\bigstar$(100%要做第二个变换) 恒等变换$x=e^{ln x},u^v=e^{ln u^v}=e^{v ln u}$三角函数
反三角函数
- $sinx$取$-\dfrac{\pi}{2}$到$\dfrac{\pi}{2}$区间做变换
- $cos x$取$0$到$\pi$区间做变换
- $f(x)=arcsin(x)+arccos(x)=\dfrac{\pi}{2}$
- $f’(x)=\dfrac{1}{\sqrt{1-x^2}}-\dfrac{1}{-\sqrt{1-x^2}} \equiv 0$
- 拉:$f(b)-f(a)=f’(g)(b-a)$
$\bigtriangledown$ $xe^x,xln(x),x^x$随手就能画出来
取整函数
- $x-1<[x]<x$
常见图像要不假思索的画出来
图像变换
平移变换
- 自变量变换:左加右减
对称变换
- 添负号
- 函数添加绝对值
- $\bigstar$ 自变量加绝对值
伸缩变换
- 自变量kx,横坐标缩小$\dfrac{1}{k}$
$\spadesuit$(p13:极坐标系下的图像) 极坐标系下的图像($g(r,\theta)=0$)
用描点法画常见图像
$\bigstar$ 心形线
- $r=a(1-cos(\theta))$
- 外摆线的一种
玫瑰线
- $r=a\cdot sin(3\theta)$
阿基米德螺线
- $r=a\cdot \theta(a>0.\theta\leq 0)$
伯努利双扭线
- $r^2=2a^2cos(2\theta)$
用直角系观点画极坐标系下图像
- 感觉好像没有想象中的那么流畅?
- 如果r随角度增大是很明显的螺旋线
参数法——参数方程
$$\left( { \begin{array}{cc} x = x(t)\ y=y(t) \end{array} \right)$$
$\bigstar$ 摆线
$${ \begin{array}{cc} x = r(t-sin(t))\ y=r(1-cos(t)) \end{array} $$
- 平摆线(在地平摆动的线)
- 周期是$\pi r$
$\bigstar$ 星形线
$${ \begin{array}{cc} x = r\cdot cos^3t\ y=r\cdot sint^3t \end{array} $$
- 内摆线
$\spadesuit$(p23:1.1.4,p24答案) 对数螺线
$r=ae^{k\theta}$
常用基础知识
数列
等差数列
首项为$a_1$,公差为$d$(d $\neq$ 0)的数列$a_1,a_1+d,\cdots,a_1+(n-1)d$
${\textstyle\unicode{x2460}}$ 通项公式 $a_n=a_1+(n-1)d$
${\textstyle\unicode{x2461}}$ 前$n$项的和$S_n=\dfrac{n}{2}[2a_1+(n-1)d]=\dfrac{n}{2}(a_1+a_n)$
$\bigstar$ 等比数列
首项为$a_1$,公比为$r(r\neq0)$的数列$a_1,a_1r,a_1r^2,\cdots,a_1r^{n-1}$
${\textstyle\unicode{x2460}}$ 通项公式$a_n=a_1r^{n-1}$
${\textstyle\unicode{x2461}}$ 前$n$项的和(n从1开始数,$\color{red}{\text{记忆}}$读法:首项乘以(1-公比的n次方),除以1-公比)
$$
S_n = \begin{cases}
na_1 ,& r=1, \
\dfrac{a_1(1-r^n)}{1-r} ,& r\neq 1,
\end{cases}
$$
- 若$|r|<1 \implies \displaystyle\lim_{n \to \infty} \dfrac{1-r^n}{1-r}=\dfrac{1}{1-r}$
一些常见数列前$n$项和
${\textstyle\unicode{x2460}}$ $\displaystyle \sum_{k=1}^n k=1+2+3+\cdot+n=\dfrac{n(n+1)}{2}$
${\textstyle\unicode{x2461}}$ $\displaystyle \sum_{k=1}^n k^2=1^2+2^2+3^2+\cdot+n^2=\dfrac{n(n+1)(2n+1)}{6}$
${\textstyle\unicode{x2462}}$ $\displaystyle \sum_{k=1}^n \dfrac{1}{k(k+1)}=\dfrac{1}{1 \times 2}+ \dfrac{1}{2 \times 3} + \dfrac{1}{3 \times 4} +\cdot+\dfrac{1}{n \times (n+1)}=\dfrac{n}{n+1}$ (列项相消)
三角函数
三角函数的基本关系
- $sec \alpha = \dfrac{1}{cos \alpha}$
- $1+tan^2=sec^2\alpha$
- $csc \alpha = \dfrac{1}{sin \alpha}$
- $cot \alpha = \dfrac{1}{tan \alpha}$
诱导公式
$\bigstar$(换元常用,自己一开始没怎么理解) 8点,奇变偶不变,符号看象限
- $sin(\dfrac{\pi}{2} \pm \alpha) = cos\alpha$
- $cos(\dfrac{\pi}{2} \pm \alpha) = \mp sin\alpha$
- $sin(\pi \pm \alpha) = \mp sin\alpha$
- $cos(\pi \pm \alpha) = - cos\alpha$
重要的公式
倍角公式
- $sin 2\alpha=2sin\alpha cos\alpha$
- $cos2\alpha=cos^2-sin^2=1-2sin^2\alpha=2cos^2\alpha-1$
- $sin 3\alpha = -4sin^2\alpha+3sin\alpha$
$\bigstar$(真题) $\text{当}x\to 0\text{时,}3sin3x-sin3x \backsim cx^k,c=?,k=?$
- 解法1:泰勒展开,幂次最低原则展开
- 解法2:$sin 3\alpha = -4sin^2\alpha+3sin\alpha$
和差公式
$tan(\alpha \pm \beta)=\dfrac{tan\alpha \pm tan \beta}{1 \mp tan\alpha tan\beta}$
- $tan(\dfrac{\pi}{4}+\alpha)$
$sin(\alpha \pm \beta)=sin\alpha cos\beta \pm cos \beta sin \alpha$
万能公式
指数运算法则
$\bigstar$ $\bigstar$ $\bigstar$(多项相乘,相除,乘方,开方) 对数运算法则
- $\spadesuit$(p65:1.4.19) $y=\sqrt[3]{\dfrac{(x+1)(2x-1)^2}{(4-3x)^5}},\text{求}y’$
- 加绝对值取对数
- 统计学里的极大似然估计法
- 见到$ln(1+\dfrac{1}{x})$ $\spadesuit$(p21:常用不等式(10))
- 拉格朗日
一元二次方程基础
${\textstyle\unicode{x2460}}$ 一元二次方程$ax^2+bx+c=0(a\neq 0)$
${\textstyle\unicode{x2461}}$根的公式$x_{1,2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$
- 讲微分方程的时候会用到加上虚部i, 共轭复根
${\textstyle\unicode{x2462}}$ 根与系数的关系(韦达定理)$x_1+x_2=-\dfrac{b}{a},x_1x_2=\dfrac{c}{a}$
因式分解公式
- $(a+b)^3=a^3+3a^2b+3ab^2+b^3$
- 系数记忆方法:1331
- $(a-b)^3=a^3-3a^2b+3ab^2-b^3$
- 二项定理$(a+b)^n=\displaystyle \sum_{k=0}^nC_n^ka^{n-k}b^k$
- 次消彼长
- $a^3+b^3 = (a+b)(a^2-ab+b^2)$
阶乘与双阶乘
- $(2n)!!=2\cdot4\cdot6\cdot \cdots \cdot(2n)=2^n\cdot n!$
- $(2n-1)!!=1\cdot3\cdot5\cdot \cdots \cdot(2n-1)$
- $\bigstar$ $\bigstar$ $\bigstar$(必考) 华里士公式(点火公式)
- 如: $\int_0^{\frac{\pi}{2}}sin^{10}xdx=\dfrac{9}{10}\dfrac{7}{8}\dfrac{5}{6}\dfrac{3}{4}\dfrac{1}{2}\dfrac{\pi}{2}$
- 如: $\int_0^{\frac{\pi}{2}}cos^{9}xdx=\dfrac{8}{9}\dfrac{6}{7}\dfrac{4}{5}\dfrac{2}{3}$
$\bigstar$ $\bigstar$ $\bigstar$ 常用不等式
$\spadesuit$(p?:例1.2.2) 设a,b为实数,则 ${\textstyle\unicode{x2460}}$ $|a\pm b| \leq |a|+|b|$; ${\textstyle\unicode{x2461}}$ $||a|-|b|| \leq |a-b|$ $\spadesuit$(p?:例1.2.2)
- 函数的极限和绝对值极限的关系
- 推广:离散,连续情况
- 绝对值不等式的记忆方法:其实稍微推导一下是很显然的对于2式子只需考虑,左边的最大比右边的最小要小即可(即符号相同,其实左边的差无所谓符号)
- 由此可以归纳出,绝对值有让数字变大的趋势,绝对值的差会让数字变小
${\textstyle\unicode{x2460}}$ $\sqrt{ab}\leq \dfrac{a+b}{2} \leq \sqrt{\dfrac{a^2+b^2}{2}}$ $\spadesuit$(p?:例题1.1.4)
- 几何平均值小于算数平均值
高等数学 ch2.数列极限
p32
数列极限
- 求极限(或证明极限的存在性)
引言
- 极限,是一个”无限趋近的过程“
- 注意是过程,不是值
| 定义法解极限题目 | 要点 |
|---|---|
 | $\spadesuit$(p27:例1.2.1) $\spadesuit$(p29:习题1.2.1)三部曲 ${\textstyle\unicode{x2460}}$ 先写距离$\lvert x_n-a\rvert < \varepsilon$(先写距离,数列通项减去a,加绝对值) ${\textstyle\unicode{x2461}}$ 反解出$n>g(\varepsilon)$ ${\textstyle\unicode{x2462}}$ 取$N=[g(\varepsilon)]+1$ |
用定义
设$\lbrace x_n \rbrace$为一数列,如果存在常数$a$,对于任意给定的正数$\varepsilon$(无论它多么小),总存在正整数$N$,使得当$n>N$时,不等式$\lvert x_n -a \rvert < \varepsilon$都成立,那么就称常数$a$是数列$\lbrace x_n \rbrace$的极限,或者称数列$\lbrace x_n \rbrace$收敛于$a$,记为
$$
\displaystyle \lim_{n \to \infty}x_n =a \quad \text{或} \quad x_n \to a(n \to \infty)
$$
- ‘$\varepsilon-N$语言’
- 数列与子列的关系
$\spadesuit$(p?:例题1.2.2)若原极限存在,则加绝对值的极限也存在
由绝对值不等式$||a|-|b|| \leq |a-b|$
但是注意右不能推左,即若加绝对值的极限也存在,原极限可能不存在
$$\text{除非}A=0,\bigstar \displaystyle\lim_{n \to \infty}a_n=0 \iff \displaystyle \lim_{n \to \infty}|a_n|=0$$
夹逼定理可以用绝对值,省去了一半的功夫
一个命题的逆否命题可以用来帮助判断(德摩根定律)
判断数列是否收敛的两个方法,用逆否命题
- 取一个子数列不收敛
- 取两个子数列没有收敛到一个数
用定义解题总结: 当给定极限为几的时候,要你证明可以尝试要用定义法
$\spadesuit$(p27:收敛数列的性质) 用性质
定理1 唯一性
给出数列${x_n}$,若$\displaystyle\lim_{n\to \infty}x_n=a$(存在),则$a$是唯一的
定理2 有界性
若数列${x_n}$极限存在,则数列${x_n}$有界
定理3 $\bigstar$(脱帽法) 保号性
设数列$\lbrace a_n \rbrace$存在极限$a$,且$a>0$(或$a<0$),,则存在正整数$N$,当$n>N$时,有$a_n>0$(或$a_n<0$)
推论 如果数列${a_n}$从某项起有$a_n\geq 0$,且$\displaystyle\lim_{n\to \infty}a_n=a$,则$a\geq 0$
(脱帽法)不带等号
$\displaystyle\lim_{n\to \infty}a_n=a>0 \implies a_n>0$
(戴帽法)通项大于0,极限(加上了帽子的限制)也大于0,始终带有一个等号
$$
a \geq 0 \impliedby \begin{cases}
a_n \geq 0 \
\text{且} \displaystyle \lim_{n \to \infty} a_n =a
\end{cases}
$$
- 即使通项严格大于零,极限有可能是0
用数列极限运算法则
数列极限的运算法则如下,即加减乘除的极限等于极限的加减乘除
设$\displaystyle \lim_{n \to \infty}x_n=a,\quad \displaystyle \lim_{n \to \infty}y_n=b$
$\displaystyle \lim_{n \to \infty}(x_n\pm y_n)=a \pm b$
$\displaystyle \lim_{n \to \infty}x_n y_n=ab$
$\displaystyle \lim_{n \to \infty}( \dfrac{x_n}{y_n} )=\dfrac{a}{b}$
推论
如果$\lim f(x)$存在,而$c$为常数,那么$\lim \lbrack cf(x) \rbrack = c\lim f(x)$
如果$\lim f(x)$存在,而$n$为正整数,那么$\lim \lbrack f(x) \rbrack^n = [\lim f(x)]^n$
注意不能拆,反例分析:
$$
\displaystyle \lim_{n \to \infty}(a_n + b_n) = 1 \nRightarrow \displaystyle \lim_{n \to \infty} a_n +\displaystyle \lim_{n \to \infty} b_n = 1
$$
例如:$a_n=(-1)^n,b_n=-(-1)^n+1$
但是已经存在是可以直接用$\spadesuit$(p?:例题1.2.4)
用数列极限运算法则解题总结:emmm,一般不会单独出吧
$\bigstar$ 用夹逼准则
如果数列${x_n},{y_n},{z_n}$满足
${\textstyle\unicode{x2460}}$ $y_n \leq x_n \leq z_n(n=1,2,3,\cdots)$
${\textstyle\unicode{x2461}}$ $\displaystyle lim_{n\to \infty}y_n=a,\quad \displaystyle lim_{n\to \infty}z_n=a$
则数列${x_n}$的极限存在,且$\displaystyle lim_{n\to \infty}x_n=a$
夹:夹逼准则不验证等号
逼:’哪里跑’
$\spadesuit$(p28:例题1.2.5)
经典的把分母放大缩小
$\spadesuit$(p?:习题1.2.2)
$\bigstar$(考研真题) $\spadesuit$(p?:习题1.2.3)
只变分母不变分子
用夹逼准则解题:表达式可以很好的放缩
$\bigstar$ $\bigstar$ $\bigstar$(考研数学压轴题的考点) 用单调有界准则
单调有界数列必有极限,即若数列${x_n}$单调增加(减少)且有上界(下界),则$\displaystyle \lim_{n \to \infty}x_n$存在
+ 单调有界数列必有极限
证明数列单调的两个方法
- 做差$x_{n+1}-x_n$
- 做比$\dfrac{x_{n+1}}{x_n} \leq 1$(同号)
$\spadesuit$(p?:1.2.6 和1.2.7)
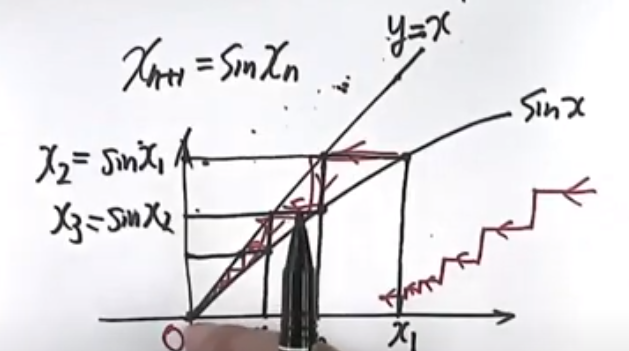
$\bigstar$ 见到递推式 $a_{n+1}=f(a_n)$一般用单调有界准则 $\mho$(还有一些别的方法)
$\blacktriangleright$(为什么还要证明$A\geq \sqrt{2}$))例题1.2.6没怎么看懂,因为求出来有正负两个值
$\bigstar$(真题) $\spadesuit$(p?:1.2.7) 取无数次sin $\spadesuit$(p21: $sinx<x$)
数学分析的思想:用迭代逼近一个数
$\flat$ $\spadesuit$(p?:例1.2.4) $\spadesuit$(p18:裂项相消)
$\bigstar$(求极限的另外一个方法直接计算出来(直接计算算法,考验恒等变化)) $\spadesuit$(p?:例题1.2.6 ) 二阶递推变成1阶递推 ,裂项相消的逆运算
用单调有界准则解题总结:
分三步
- 证明单调:
- 求导
- 做差的极限小于0
- 证明有界:
- 不等式
- 求极限值:
- 等式两边取极限
适用题型:给递推式
用定积分的定义
如例1.8.23
高等数学 ch3.函数极限与连续性
p39
$\bigstar$(学习方法) 对知识结构的把握,纲举目张
运算法则-无穷小比阶来研究7种未定式计算
函数极限
方法一览
定义
局部有界性
局部保号性
强调计算
领域
一维的情况
可以叫区间
- 领域:以$x_0$为中心的任何开区间称为点$x_0$的领域,记作$U(x_0)$
- $\delta$领域:记作$U(x_0,\delta)$
- 去心$\delta$领域:记作$\mathring{U}(x_0,\delta)$
二维的情况
以$p$为圆心,圆内的点就是其领域,可以叫区域
- $\delta$领域:记作$U(p_0,\delta)$
定义
设函数$f(x)$在点$x_0$的某一去心领域内有定义.如果存在常数$A$,对于给定的正数$\varepsilon$(无论它多么小),总存在正数$\delta$,使得$x$满足不等式$0 \lvert x-x_0 \rvert < \delta$时,对应的函数值$f(x)$都满足不等式
$$
\lvert f(x) -A \rvert < \varepsilon
$$
那么常数$A$就叫做函数$f(x)$当$x \to x_0$时的极限,记作
$$
\lim_{x \to x_0}f(x)=A \text{或} f(x) \to A \quad (\text{当}x \to x_0)
$$
可以简单的表述为
$$
\lim_{x \to x_0}f(x) = A \iff \forall \varepsilon >0, \exists \delta > 0,\text{当}0< \lvert x - x_0\rvert < \delta \text{时,有} \lvert f(x)-A \rvert < \varepsilon
$$
左极限:
$$
\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists \delta > 0,\text{当} x_0 - \delta < x <x_0 \text{时,有} \lvert f(x)-A \rvert < \varepsilon
$$
右极限:
$$
\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists \delta > 0,\text{当} x_0 < x < x_0 - \delta \text{时,有} \lvert f(x)-A \rvert < \varepsilon
$$
自变量趋于无穷大的极限:
$$
\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists X > 0,\text{当} \lvert x \rvert > X \text{时,有} \lvert f(x)-A \rvert < \varepsilon
$$
自变量趋于负无穷大的极限:
$$
\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists X > 0,\text{当} x < -X \text{时,有} \lvert f(x)-A \rvert < \varepsilon
$$
自变量趋于正无穷大的极限:
$$
\lim_{x \to x_0^-}f(x) = A \iff \forall \varepsilon >0, \exists X > 0,\text{当} x > X \text{时,有} \lvert f(x)-A \rvert < \varepsilon
$$
‘$\varepsilon-\delta$语言’
‘$\varepsilon-X$语言’,总共四种要整理一下
极限和函数的值没有任何关系
性质
$\bigstar$(真题) $\spadesuit$(p?:例题1.3.1)
- 考虑趋向于$0^+和0^-的两种情况$
- 极限的和等于和的极限的前提 $\mho$(前提是啥来着)
唯一性 $\bigstar$
如果$\lim_{x \to x_0}\text{存在}$,那么这极限唯一
局部有界性 $\bigstar$
如果$\lim_{x \to x_0}f(x)=A,$那么存在常数$M>0$和$\delta>0$,使得当$0< \lvert x - x_0 \rvert < \delta\text{时,有}\lvert f(x) \rvert \leq M$
- 有限个有界的函数和差积依然是有界函数,如果是无限个的话就变成了级数
- $\spadesuit$(p6:(5)7行)需要倒背如流,第七个用拉格朗日去证
- 拉格朗日的作用,导数为0和导数为正无穷,导数值决定了函数值(证明)
- $\bigstar$(真题) $\spadesuit$(p?:1.3.2 ) 排除法
局部保号性 $\bigstar$
如果 $\lim_{x \to x_0}f(x)=A,且$A>0$(或$A<0$),那么存在常数$\delta >0$,使得当$0< \lvert x - x_0 \rvert < \delta$是,有$f(x)>0$(或$f(x)<0$)
戴帽法 极具区分度,一定要记准确
运算法则
定理1 两个无穷小的和是无穷下
推广:有限个无穷小的和也是无穷小
定理2 有界函数与无穷小的乘积是无穷小
推论1 常数与无穷小的乘积是无穷小
推论2 有限个无穷小的乘积是无穷小
定理3 加减乘除的极限等于极限的加减乘除
如果 $\lim f(x)=A, \lim g(x)=B$那么
(1) $\lim \lbrack f(x) \pm g(x) \rbrack =\lim f(x) \pm \lim g(x)=A \pm B$
(2) $\lim \lbrack f(x) \cdot g(x) \rbrack =\lim f(x) \cdot \lim g(x)=A \cdot B$
(3) 若又有$B \neq 0,\text{则}$
$$
\lim \dfrac{f(x)}{g(x)}= \dfrac{\lim f(x)}{\lim g(x)}= \dfrac{A}{B}
$$
推论1 如果$\lim f(x)$存在,而$c$为常数,那么$\lim \lbrack cf(x) \rbrack = c\lim f(x)$
推论2 如果$\lim f(x)$存在,而$n$为正整数,那么$\lim \lbrack f(x) \rbrack^n = [\lim f(x)]^n$
定理6(复合函数的极限运算法则)
设函数$y=f\lbrack g(x) \rbrack$是由函数$u=g(x)$与函数$y=f(u)$复合而成,$f\lbrack g(x) \rbrack \text{在点}x_0$的某去心领域内有定义,若$\displaystyle \lim_{x \to x_0}g(x)=u_0, \displaystyle \lim_{u \to u_0}f(u)=A\text{,且存在}x \in \mathring{U}(x_0,\delta_0)\text{时,有}g(x) \neq u_0$则
$$
\displaystyle \lim_{x \to x_0} f\lbrack g(x) \rbrack =\displaystyle \lim_{u \to u_0}f(u)=A
$$
如果两个函数的极限存在,那么对应极限的加减乘除等于对饮加减乘除的极限 + 注意除法,分母不能是0
夹逼准则
- 既可以是一个数也可以是无穷大
- 夹逼准则很精彩
- $x-1<[x] \leq x$
洛必达法则
法则一
必须满足下面三个条件
两个函数都趋向于0
${\textstyle\unicode{x2460}}$ 两个函数可导
两个函数相除的极限存在,趋向于0或者无穷大
$$
\text{则}\displaystyle \lim_{x \to \cdot} \dfrac{f(x)}{F(x)} \buildrel \rm \dfrac{0}{0} \text{或者} \dfrac{\infty}{\infty}\over{=} \displaystyle \lim_{x \to \cdot} \dfrac{f’(x)}{F’(x)}
$$
第三点条件很重要,一个反例
右边存在左边必定存在,反之不然
常识性问题$\displaystyle \int_0^\pi sin(x)dx=2$
$$\displaystyle \lim_{x \to + \infty} \dfrac{\displaystyle \int_a^x |sin(x)|dt}{x} \buildrel \rm \dfrac{\infty}{\infty}\over{=}\displaystyle \lim_{x \to + \infty} \dfrac{|sin(x)|}{1}$$
泰勒公式 $\bigstar$ $\bigstar$ $\bigstar$
公式
$sin(x)$是奇函数,展开绝对没有偶函数
掌握无穷小的计算规则 $\spadesuit$(p38: 掌握无穷小的计算规则)
$\dfrac{A}{B}$ $\bigstar$(考研真题) $\spadesuit$(p36:考研真题)
展开原则
$A-B$型,展开至系数不相等的$k$次幂
常见的等价变化,$\spadesuit$(p38:常见的等价变化)
强调的两个等价变换
- $x + sin(x)\backsim 2x$
- $x - sin(x)\backsim \dfrac{1}{6}x^3$
归结原则(函数极限与数列极限的关系)
如果极限$\displaystyle \lim_{x \to x_0}f(x)$存在,$\lbrace x_n \rbrace$为函数$f(x)$的定义域内任一收敛于$x_0$的数列,且满足:$x_n \neq x_0(n \in N_+)$,那么相应的函数值数列$\lbrace f(x_n) \rbrace$必收敛,且$\displaystyle \lim_{n \to \infty}f(x_n)=\displaystyle \lim_{x \to x_0}f(x)$
海涅定理:联系离散和连续的常识
海涅定理只用不证
右推课本的例子
$\bigstar$(真题) $\spadesuit$(p?:例题1.3.14) 左推
- 幂值函数写成$u^v=e^{vlnu}$
- $ln(1+g(x)) \backsim g(x),g(x) \to 0$
- $lnu = ln(1+u-1) \to u-1,u \to 1$
无穷小比阶(题型)
- 无穷大和极限都是一个过程
- 不是所有的无穷小都能比阶 $\mho$(反例,书本上的)
七种未定式的计算
$\dfrac{0}{0}\text{0比0} ,\quad$ $\dfrac{\infty}{\infty} \text{无穷比无穷},\quad$ $\infty \cdot 0\text{无穷乘0}$
$\infty - \infty\text{无穷减无穷}$,
$\infty^0\text{无穷的0次方}, \quad0^0\text{0的0次方}, \quad1^{\infty}\text{1的无穷次方}$
5种方法
- 四则运算方法
- 洛必达法则
- 泰勒公式
- 归结原则
- 夹逼准则
第一步:化简
- $e^{f(x)}-e^{g(x)}=e^{g(x)}[e^{f(x)-g(x)}-1] \backsim f(x)-g(x)$
- $e^{sin(x)}-e^{(x)}=sin(x)-x=-\dfrac{1}{6}x^3$
第二步判断类型:7种中的一种
$\dfrac{0}{0}$,$\dfrac{\infty}{\infty}$
- 洛必达
- 泰勒展开
$\spadesuit$(p?:例1.3.3)
- 上面次数高,地面次数低,方便运算
- 倒代换
$\spadesuit$(p?:例1.3.6)
- $\infty \cdot 0$
- $\sqrt{a}-\sqrt{b}$
- 注意负代换
$\bigstar$(题目的结论要记住) $\spadesuit$(p?:例1.3.7)
- 设置分母有原则,简单因式才下放
- 简单:$x^\alpha ,x^{\beta x}$
- 复杂:$ln(x),arcsin(x),arctan(x)$
$\spadesuit$(p?:例1.3.8) 泰勒展开
$\infty - \infty$
- 因式分解
- 通分(创造分母通分)
- 转换成0/0
- 和差化积
$$
\infty - \infty =
\begin{cases}
(1) & \text{有分母,则通分} \cr
(2) & \text{没有分母,创造分母,再通分(倒代换)}
\end{cases}
$$
$\spadesuit$(p?:1.3.10 )
- 有分母则同分
$\spadesuit$(p?:例1.3.11)
- 没有分母,创造分母再通分
- $e^x-1-x \backsim \dfrac{1}{2}x^2(x \to 0)$
$\infty^0,0^0,1^{\infty}$
- 幂指函数
$\spadesuit$(p?:例1.3.12)
- $\infty^0$
- $\bigstar$(必考题) $(ln(x+\sqrt{1+x^2}))’=\dfrac{1}{\sqrt{1+x^2}}$
$\spadesuit$(p?:例1.3.13,例1.3.14 $1^\infty$)
- $lim u^v$ $\buildrel \rm \dfrac{1}{\infty}\over{=}$ $e^{lim v lnu}=e^{lim v(u-1)}$
连续与间断
- 是函数极限的应用
- 连续和间断是逐点的概念
- 考题只看两类点
- 分段函数的分段点$\spadesuit$(p?:例1.3.20) $\spadesuit$(p?:例1.3.21)
- $\bigstar$ 函数的无定义点$\spadesuit$(p?:例1.3.22)
$\spadesuit$(p?:例1.3.20)
连续点的定义
- 极限值=函数值,连续
间断点的定义与分类
设函数$f(x)$再点$x_0$的某去心领域内有定义(前提, 极限是一个过程)
- $\color{green}{\text{可去间断点}}$ 、 $\color{green}{\text{跳跃间断点}}$ 是 $\color{red}{\text{第一类间断点}}$
- $\color{green}{\text{无穷间断点}}$ 、 $\color{green}{\text{震荡间断点}}$ 是 $\color{red}{\text{第二类间断点}}$
- $\displaystyle \lim_{x \to 0^+ }xln(x)$
- $\blacktriangleright$(明明求导的时候x趋向0的速度是1,lnx趋向0的速度是无穷大,为什么其极限还是0)
$\sharp$ 菲赫金哥尔茨微积分教程
可去间断点
也叫可补间断点
两种情况
- 若$\displaystyle \lim_{x\to x_0}f(x) = A \neq f(x_0)$
- $f(x)$无定义
跳跃间断点
极限有两个值,跳跃间断点
无穷间断点
$\displaystyle \lim_{x \to x_0}f(x) = \infty$
- 至少一个为无穷大
震荡间断点
$\displaystyle \lim_{x \to x_0}f(x)$ = 震荡不存在
- $\displaystyle \lim_{x \to x_0}sin \dfrac{1}{x}$
高等数学 ch4.一元函数微分学的概念与计算
- 知识结构:概念,计算,应用
$\mho$(函数可导,导函数必定连续?)
概念
引例
导数的概念
- $\displaystyle \lim_{x \to 0} \dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$
- 角点
- $f(x)=x^{\frac{1}{3}}$在$x=0$处的切线问题
- 连续不一定可导
$\spadesuit$(p6:7个结论)
- $\spadesuit$(p60:例1.4.1)
- 用定义
- -0=+0
$\bigstar$(真题) $\spadesuit$(p61:例1.4.3)
$\bigstar$(真题) $(uv)’=u’v+uv’$
$\mho$(补充完过程)
$$
\begin{split} (uv)’ &=\displaystyle \lim_{\Delta x \to 0} \dfrac{f(x+\Delta x)-f(x)}{\Delta x} \cr
&=\displaystyle \lim_{\Delta x \to 0} \dfrac{u(x+\Delta x)v(x+\Delta x)-u(x)v(x)}{\Delta x} \cr
&=
\end{split}
$$
$\flat$(定理证明) 猜题:费马定理,牛顿莱布尼茨公式
$\spadesuit$(p61:例1.4.3)
错误的选项的方法:举反例
微分的概念
一元微积分一个东西在动,其他都不能动
- 增量$\Delta y=f(x_0+\Delta x)-f(x_0)=A\Delta x + o(\Delta x)$
- 线性主部(微分)+误差
$\spadesuit$(p?:例1.4.7)
导数与微分的计算
$\bigstar$(热点) $\spadesuit$(p62:例1.4.8)
$\bigstar$(结论) $(ln(|x|))’=\dfrac{1}{x}$视绝对值而不见
- 导数除以其自己积分的原函数是$ln(u(x))$
- 可导必连续,连续导数值等于函数值
- 直接链式求导
- 先复合再求导
四则运算
- $(uv)\prime=\dfrac{u\prime v-uv\prime}{v^2}$
分段函数的导数
- ${\textstyle\unicode{x2460}}$ 在分段点用导数定义法求导数是否存在
- $\blacktriangleright$(为什么不能用求导公式)[难道是之前解释过的领域才有极限的概念]
- ${\textstyle\unicode{x2461}}$ 非分段点,用导数公式
复合函数的导数与微分形式不变性
- 微分形式不变 $df(\text{狗})=f’(\text{狗})d\text{狗}$
- 二阶微分形式没有这个性质
反函数的导数
- $\varphi’(y)=\dfrac{1}{f’(x)},\varphi’’(y)=-\dfrac{f’’(x)}{ [ f’(x) ]^3 }$
- $\spadesuit$(p4:反函数) 有反函数的充分条件是单调
- $\spadesuit$(p91:例题1.6.8) $f’(x)$必保号
- 达布定理(有正有负必有零点)
- $\blacktriangleright$(?1.6.8导数零点定理和达布定理有关系吗)
- $\spadesuit$(p64:例1.4.15)
- $\clubsuit$ 变限积分函数 $\spadesuit$(p60:10)
- $S’(x)=\displaystyle \int_{\varphi_1(x)}^{\varphi_2(x)}g(t)dt=g[\varphi_2(x)]\cdot \varphi_2’(x)-g[\varphi_1(x)]\cdot\varphi_1’(x)$
- $\sharp$
- $dx\cdot dx=dx^2$ 叫微分的幂
- $2xdx=d(x^2)$叫 幂的微分
- p62
- $\bigtriangledown$ $y_x’$指的是y对x求导,$y_{xx}’’$指的是y对x求二阶导,$x_y’$指的是x对y求导
- $\mho$(反函数的工程意义)
参数方程所确定的函数的导数
- $\spadesuit$(p65:例1.4.17) 二阶导
隐函数求导法
$\bigstar$(一天不能停)
- 公式法
- $F(x,y)=0$,$F’(x,y)=-\dfrac{F’x}{F’y}$
- 两边求导
$\bigstar$(使用性强) 对数求导法
图片详情

$\spadesuit$(p65:例1.4.19)
- $ln$加绝对值求导可以视绝对值不变
$\bigstar$(命题要素) 幂指函数求导法
例题1

例题2

- $\spadesuit$(p66:例题1.4.20)
- $y=x^x$
- $\mho$(画图) $xe^{\frac{1}{x}}$
高阶导数
归纳法
图片详情

$\spadesuit$(p66:例1.4.22)
- 直接归纳
$\spadesuit$(p67:例1.4.23)下面的框框
- 用诱导公式
莱布尼茨公式
图片详情

- 牛顿的二项展开
泰勒公式
- 零点展开叫麦克劳林公式
- 非零点叫泰勒公式
变限积分求导公式
基本求导公式
| 公式 | 题目 |
|---|---|
| $(x^a)\prime=ax^{a-1}\text{(a为常数)}$ | |
| $(a^x)\prime=a^xlna(a>0,a\neq 1)$ | |
| $(e^x)\prime=e^x$ | |
| $(log_ax)\prime=\dfrac{1}{xlna}(a>0,a\neq 1)$ | |
| $(ln x)\prime=\dfrac{1}{x}$ | |
| $(sin x)\prime=cos x$ | |
| $(cos x)\prime=-sin x$ | |
| $(arcsin x)\prime=\dfrac{1}{\sqrt{1-x^2}}$ | |
| $(arccos x)\prime=-\dfrac{1}{\sqrt{1-x^2}}$ | |
| $(tan x)\prime=sec^2x$ | 1 |
| $(cot x)\prime=-csc^2x$ | |
| $(arctan x)\prime=\dfrac{1}{1+x^2}$ | |
| $(arccot x)\prime=-\dfrac{1}{1+x^2}$ | |
| $(sec x)\prime=sec x tan x$ | |
| $(csc x)\prime=-csc x cot x$ | |
| $[ln(x + \sqrt{x^2+1})]’=\dfrac{1}{\sqrt{x^2+1}}$ | |
| $[ln(x + \sqrt{x^2-1})]’=\dfrac{1}{\sqrt{x^2-1}}$ |
跟 $\color{red}{\text{cos}}$ 相似度高的都会出现 $\color{green}{\text{负号}}$